时间复杂度与空间复杂度

18年互联网寒冬，特别是游戏行业，版号一年没发。待经济春暖花开之时，也让自己在行业行业中增加竞争力。

为什么要进行复杂度分析？
1.和性能测试相比， 复杂度分析有不依赖执行环境、 成本低、 效率高、 易操作、 指导性强的特点。
2.掌握复杂度分析， 将能编写出性能更优的代码， 有利于降低系统开发和维护成本。

时间复杂度：时间复杂度是衡量一个算法重要的指标之一，当数据量越大，算法的效率也就越能体现出来，以时间复杂度为例， 由于时间复杂度描述的是算法执行时间与数据规模的增长变化趋势， 所以常量阶、 低阶以及系数实际上对这种增长趋势不产决定性影响， 所以在做时间复杂度分析时忽略这些项。

时间负责度特点如下：

• 只关注循环执行最多的一段代码
• 加法原则，总复杂度等于量级最大的复杂度
• 嵌套代码的复杂度等于嵌套内代码复杂度的乘积

俗称：

　　1） 单段代码看高频： 比如循环。
　　2） 多段代码取最大： 比如一段代码中有单循环和多重循环， 那么取多重循环的复杂度。
　　3） 嵌套代码求乘积： 比如递归、 多重循环等
　　4） 多个规模求加法： 比如方法有两个参数控制两个循环的次数， 那么这时就取二者复杂度相加。
常用的复杂度级别：
　　多项式阶： 随着数据规模的增长， 算法的执行时间和空间占用， 按照多项式的比例增长。 包括，O(1)（常数阶） 、 O(logn)（对数阶） 、 O(n)（线性阶） 、 O(nlogn)（线性对数阶） 、 O(n^2)（平方阶） 、 O(n^3)（立方阶）。
　　非多项式阶： 随着数据规模的增长， 算法的执行时间和空间占用暴增， 这类算法性能极差。 包括，O(2^n)（指数阶） 、 O(n!)（阶乘阶） 。

最好、平均、最坏、均摊时间复杂度：

　　

// n 表示数组 array 的长度
int find(int[] array, int n, int x) {
　　int i = 0;
　　int pos = -1;
　　for (; i < n; ++i) {
　　　　if (array[i] == x) {
　　　　　　pos = i;
　　　　　　break;
　　　　}
　　}
　　return pos;
}

　　这段代码中假如寻找的这个数据正好在数组中下标为0的位置，时间复杂度为O（1），也就是最好时间复杂度。假如这个数据中没有这个数据，需要把整个数组遍历一遍，

时间复杂度为O（n）也就是最坏的时间复杂度。

　　考虑到这两种情况都比较极端，假设要查找的这个数据在数组中和不在数组中的的概率都为1/2,要查找的数据出现在数组0~n-1中的概率也是一样的为1/n，根据概率的乘法

原则，要查找的数据出现在0~n-1中的概率为1/2n。如果我们把每种情况发生的概率也算进入，平均时间复杂度的公式就变成这样了：

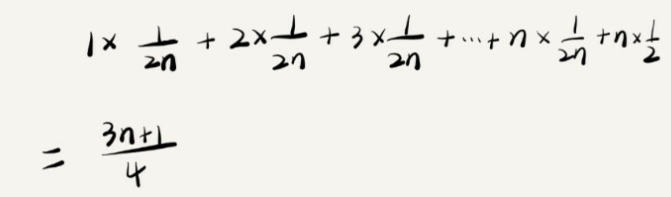
这个值就是概率论中的加权平均值，去掉常亮和系数的结果就是O(n)所以平均时间复杂度也为O(n)。

均摊时间复杂度：

// array 表示一个长度为 n 的数组
// 代码中的 array.length 就等于 n
int[] array = new int[n];
int count = 0;
void insert(int val) {
if (count == array.length) {
    int sum = 0;
    for (int i = 0; i < array.length; ++i) {
    　　sum = sum + array[i];
　　 } 
　　array[0] = sum;
　　count = 1;
}
 　　array[count] = val;
　　++count;
}    

这个算法在比较在绝大部分情况下时间复杂度都是0（1），只有在某种极端的情况下时间复杂度才是O（n），第二个不同之处在于一都是经过一个O（n）的插入之后在经过n-1个0（1）的插入，循环往复。所以可以把耗时最多一次操作，均摊到n-1个操作中，经过均摊后，这个算法的时间复杂度就是O(1)。这就是比较少见的情况下的均摊时间复杂度。

空间复杂度：

　　算法的指标中空间复杂度也是一个重要的指标。空间复杂度的全称是渐进空间复杂度，表示算法的存储空间与数据规模之间的增长关系。

　　我们常见的空间复杂度就是 O(1)、 O(n)、 O(n )， 像 O(logn)、 O(nlogn) 这样的对数阶复杂度平时很少用。