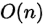剑指Offer_#43_1~n整数中1出现的次数
Contents
题目
输入一个整数 n ,求1~n这n个整数的十进制表示中1出现的次数。
例如,输入12,1~12这些整数中包含1 的数字有1、10、11和12,1一共出现了5次。
示例 1:
输入:n = 12
输出:5示例 2:
输入:n = 13
输出:6限制:
1 <= n < 2^31思路分析
这题参考了评论区大佬的题解,以下的图解也是搬运过来的。
整体的思路是,把在每一位上出现1的次数计算出来,然后相加。
那么问题关键就在于如何计算每一位出现1的次数?
一个结论:如何数出每一位出现1的次数?
如何计算0010~2219范围内,1在十位出现的次数?
首先可以把0010~2219范围内,十位是1的所有数字枚举出来。
0010,0011,...0019(1在十位出现10次)
0110,0111,...0119(1在十位出现10次)
...
0910,0911,...0919(1在十位出现10次)
1010,1011,...1019(1在十位出现10次)
...
1910,1911,...1919(1在十位出现10次)
2010,2011,...2019(1在十位出现10次)
2110,2111,...2119(1在十位出现10次)
2210,2211,...2219(1在十位出现10次)可以看到高位(前两位)的变化范围是00~22,有23种选择。
固定高位是某一种情况时,低位(个位)变化范围是0~9,有10种选择。
高位和低位组合,就有23*10=230种组合。
总结规律,你会发现,其实可以把0010~2219里的十位数字直接“抠”掉,剩下的就是000~229,一共就是230个数字。
因为十位上面的1已经是固定的,所以其实000~229里的每个数,和上面所枚举的230个数字是一一对应的。比如000对应着0010,001对应着0011...所以000~229范围内数字的个数,就是0010~2219范围内十位出现1的数字个数。
寻找规律,总结为数学表达式
理解了上面的结论,可以观察到以下的规律(图解来自评论区题解)
cur == 0

cur == 1

cur > 1

循环变量的初始化和更新
初始化
high = n // 10
cur = n % 10
low = 0
digit = 1 # 个位更新
while high != 0 or cur != 0: # 当 high 和 cur 同时为 0 时,说明已经越过最高位,因此跳出
low += cur * digit # 将 cur 加入 low ,组成下轮 low
cur = high % 10 # 下轮 cur 是本轮 high 的最低位
high //= 10 # 将本轮 high 最低位删除,得到下轮 high
digit *= 10 # 位因子每轮 × 10解答
class Solution {
public int countDigitOne(int n) {
int res = 0;
//初始化高位high,低位low,当前位cur
int high = n / 10;//除去个位
int cur = n % 10;//个位
int low = 0;//个位没有低位
//digit表示当前位的数量级,比如个位的digit是1,十位的digit是10
int digit = 1;
//high和cur同时为0,表明已经越过了最高位,停止循环
while(high != 0 || cur != 0){
//计算cur位上出现1的次数
if(cur == 0) res += high * digit;
else if(cur == 1) res += high * digit + low + 1;
else res += (high + 1) * digit;
//更新变量low,high,cur,digit
low += cur * digit;//cur变成low的一部分
cur = high % 10;//高位的最后一位变成cur
high /= 10;//high去除最后一位
digit *= 10;//数量级乘10
}
return res;
}
}时间复杂度是