P4017 最大食物链计数（拓扑排序+邻接矩阵（表））

题目背景

你知道食物链吗？Delia 生物考试的时候，数食物链条数的题目全都错了，因为她总是重复数了几条或漏掉了几条。于是她来就来求助你，然而你也不会啊！写一个程序来帮帮她吧。

题目描述

给你一个食物网，你要求出这个食物网中最大食物链的数量。

（这里的“最大食物链”，指的是生物学意义上的食物链，即最左端是不会捕食其他生物的生产者，最右端是不会被其他生物捕食的消费者）

输入格式

第一行，两个正数n、m，表示生物种类n和吃与被吃的关系数m。

接下来m行，每行两个正数，表示被吃的生物A和吃A的生物B。

输出格式

一行一个整数，为最大食物链数量模上80112002的结果。

输入输出样例

输入 #1

5 7
1 2
1 3
2 3
3 5
2 5
4 5
3 4

输出 #1

5

说明/提示

各测试点满足以下约定：

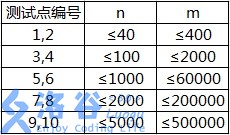
【补充说明】

数据中不会出现环，满足生物学的要求。

时间限制1s，结果模上80112002.

思路：

　　此题所找的是总食物链的长度，实际上翻译过来就是找到所有入度为0对应出度为0的链的长度，这一思想恰好满足拓扑排序的性质（具体拓扑排序见同一分类下另一篇帖子）。因此此处首先采用邻接矩阵+拓扑排序的方法去实现（别用dfs效率太低，基本的不剪枝的只过两个测试点）

实现代码（邻接矩阵）：

#include<bits/stdc++.h>
using namespace std;

//思想：邻接矩阵+拓扑排序 ，此题可以用dfs实现，但效率十分低下 
//我们需要知道，到点i的路径之和等于结点i直接连接的前驱结点的所有路径之和
//例如f[i]=f[a]+f[b]+f[c]+……    假设a b c……是点i的前驱结点（其实是有分治思想） 
int mapp[5001][5001];        //记录结点间的关系
int ru[5001];                //记录每个结点有几个入度
int chu[5001];                //记录每个结点有几个出度
int f[5001]={0};                //f[i]记录到结点i时共有多少条路径 
int sum=0;                    //记录总路径数量 
queue<int> q;                //保存入度为0的结点
int n,m;

int main(){
    int n,m;
    cin>>n>>m;
    
    for(int i=1;i<=m;i++){    //此步骤是输入+构图部分 
        int t1,t2;
        cin>>t1>>t2;
        mapp[t1][t2]=1;        //代表t1 t2结点之间有连接 
        ru[t2]++;
        chu[t1]++;
    }
    
    for(int i=1;i<=n;i++){    //最初将所有入度为0的点入队（符合拓扑排序思想） 
        if(ru[i]==0){
            q.push(i);        //入队 
            f[i]=1;            //起始点先写入一个长度 
        } 
    } 
    
    //入完队后接下来开始从入度为0的结点操作
    while(!q.empty()){
        int temp=q.front();    //所有的temp都只有后继点，而没有前驱结点,而且temp后面直接连接的后继结点至少有一个 
        q.pop();
        
        for(int i=1;i<=n;i++){    //从1~n搜索那些是它后面的点（即捕食者） 
            if(mapp[temp][i]==0)    continue;        //表示没有连接 
            f[i]+=f[temp];
            f[i]%=80112002;
            ru[i]--;
            if(ru[i]==0){        //表示此时点i的入度为0 此时可以入队     
                if(chu[i]==0){    //判断是否出度为0 若为0表示此条链搜索完毕  
                    sum+=f[i];        //加上以点i为终点的所有路径数量 
                    sum%=80112002;
                    continue;
                }
                q.push(i);        //满足入度为0就入队 
            }      
        }
    } 
    cout<<sum;
    return 0;
} 

此代码的时间/空间为942ms / 94.05MB。（基本快卡测试的边缘了）

为了稍微快一点小一点采取了邻接表的方法（其实也没变得特别快，感觉scanf的作用还比较大），算法和上面基本不变，改动不多

#include<bits/stdc++.h>
using namespace std;

//上面用邻接矩阵的方式实现拓扑排序，但要空间和时间更优以满足更加严格的限制条件时，
//采用邻接表的方法或许会更好,顺便自己练习实现邻接表
//说道邻接表，网上一大堆邻接表的模板（C++和java)，对于C++和java并没有那么熟悉的菜鸡想实现邻接表目前找到的较好的方法就是直接通过结构体构建了。
struct node{
    int ru;
    int chu;
    int f;
    int mapp[5001];            //记录后继结点
    int t;                    //记录后继结点个数 
}a[5001];
int sum=0;
queue<int> q;                //保存入度为0的结点
int n,m;

int main(){
    int n,m;
    cin>>n>>m;
    
    for(int i=1;i<=m;i++){    //此步骤是输入+构图部分 
        int t1,t2;
        scanf("%d%d",&t1,&t2);
//        cin>>t1>>t2;
        a[t1].mapp[a[t1].t++]=t2;        //代表t1 t2结点之间有连接 
        a[t2].ru++;
        a[t1].chu++;
    }
    for(int i=1;i<=n;i++){    //最初将所有入度为0的点入队（符合拓扑排序思想） 
        if(a[i].ru==0){
            q.push(i);        //入队 
            a[i].f=1;            //起始点先写入一个长度 
        } 
    }
    
    while(!q.empty()){
        int temp=q.front();    //所有的temp都只有后继点，而没有前驱结点,而且temp后面直接连接的后继结点至少有一个 
        q.pop();
        
        for(int i=0;i<a[temp].t;i++){    //从1~n搜索那些是它后面的点（即捕食者） 
            a[a[temp].mapp[i]].f+=a[temp].f;
            a[a[temp].mapp[i]].f%=80112002;
            a[a[temp].mapp[i]].ru--;
            if(a[a[temp].mapp[i]].ru==0){        //表示此时点i的入度为0 此时可以入队     
                if(a[a[temp].mapp[i]].chu==0){    //判断是否出度为0 若为0表示此条链搜索完毕  
                    sum+=a[a[temp].mapp[i]].f;        //加上以点i为终点的所有路径数量 
                    sum%=80112002;
                    continue;
                }
                q.push(a[temp].mapp[i]);        //满足入度为0就入队 
            }      
        }
    } 
    cout<<sum;
    return 0;
} 

时间/空间： 390ms / 22.25MB（还是能明显看见优化的:)