朴素贝叶斯是一组简单快速的分类算法。下面来介绍一下它的原理。
在机器学习中，我们有时需要解决分类问题。也就是说，给定一个样本的特征值（feature1,feature2,...feauren），我们想知道该样本属于哪个分类标签（label1,label2,...labeln）。即：我们想要知道该样本各个标签的条件概率P(label|features)是多少，这样我们就可以知道该样本属于哪个分类。例如：假设数据集一共有2个分类（标签），如果现在出现一个新的样本，其P(label1|featurenew_sample)>P(label2|featurenew_sample)，那么我们就可以判定该样本的标签为label1。
那么P(label|feature)该如何计算呢？我们首先可以假设数据符合某一种分布，然后估计出分布的参数，然后我们就可以得出在该参数下，某新样本特征x对应的目标y的可能性有多大了。有以下三种估计方法，分别是：极大似然估计法（MLE），贝叶斯估计法（Bayesian），极大后验概率估计法（MAP）。（图片摘自：https://www.cnblogs.com/little-YTMM/p/5399532.html）
（一）极大似然估计法（MLE, maximum likelihood estimation）
属于频率学派，认为存在唯一真值θ。
如果我们对总体进行取样，我们假设取样出的数据符合某一种分布（比如说正态分布），但是我们不知道这个分布的参数θ（比如说平均值，标准差)，极大似然估计法就是去找到能使模型产生出样本数据的概率最大的参数θ，也就是找到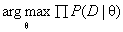
。由于
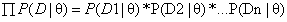有连乘运算，通常对似然函数取对数计算，就可以把连乘变成求和，然后求导，取导数为0的极值点，就是想找的参数值。
但是极大似然估计只适用于数据量大的情况。如果数据量较小，结果很可能会产生偏差。举个简单的例子，假如把一个均匀的硬币抛10次，有7次正面朝上，3次反面朝上（假设数据服从伯努利分布）。那么这个伯努利概率分布函数就是P(D|Head)=P(Head)7*(1-P(Head))3，函数在p(Head)=0.7时达到最大。那么我们能说P(Head)=0.7吗？这个结果肯定不准，因为我们都知道P(Head)=P(Tail)=0.5。但是如果我们把这个硬币抛1000次，得出的结果就会较准确了。但是现实中，很多时候，我们无法做那么多次试验。对此，解决的办法就是贝叶斯估计法。
（二）贝叶斯估计法（Bayesian estimation）
属于贝叶斯学派，认为θ是一个随机变量，符合一定的概率分布。
还是对总体进行取样，我们假设取样出的数据符合某一种分布，而且根据以往的经验，我们知道参数θ的概率分布（P(θ)也即先验概率），我们根据贝叶斯定理得到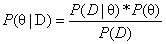
，这样通过学习条件概率P(D|θ)的分布，就可以计算出后验概率P(θ|D)的分布。对新样本预测时考虑所有可能的θ，所以可以得到最优的预测结果。
还是用上面抛硬币的例子，我们仍然假设数据服从伯努利分布，而且根据以往的经验，我们知道抛100次硬币，应该有50次正面朝上，50次反面朝上，通过这个先验知识，我们可以计算得出后验概率P(Head|D)的概率分布函数为P(Head|D)=p(Head)57*(1-p(Head))53，我们将可能的参数（p(Head)概率从0-1）代入，计算可知函数在P(Head)=0.518附近达到峰值。通过加入先验概率，我们得出的预测结果要更准确。这说明，贝叶斯估计可以用于数据量较少或者比较稀疏的情况。
然而，我们发现贝叶斯估计法虽然解决了数据量较少的问题，但是又带来了新的问题。因为在用贝叶斯估计法解决问题的时候，我们让参数θ服从某种概率密度函数分布，这就会导致计算过程高度复杂。人们为了计算上的方便，就提出不再把所有的后验概率p(θ|D)都找出来，而是采用类似极大似然估计的思想，找到极大后验概率，这种简单有效的方法叫做极大后验概率估计法。
（三）极大后验概率估计法（MAP, maximum a posterior probability estimation）
极大后验概率估计法与极大似然估计法类似，只是加入了先验概率P(θ)，相当于增加一种惩罚（正则化），以减少偏差。
（注：如果先验概率P(θ)是均匀分布的，那么极大后验概率估计法等价于极大似然估计法。）
极大后验概率估计法与贝叶斯估计法的区别在于：极大后验概率估计法是用极大似然估计法对条件概率进行估计，估计出条件概率的最大值，从而找到后验概率的最大值；而贝叶斯估计法是假设先验概率服从某种分布，计算出所有可能的后验概率，也就是说找出后验概率的分布。
朴素贝叶斯使用的是极大后验概率估计法，这就相当于通过学习训练集数据特征X和目标y的联合分布P(label, features)来推导出后验概率P(label|features)的分布，然后用最大似然估计法对新样本的后验概率P(label|feature)进行估计。首先对数据集P(features|label)的分布进行假设，这样我们就知道了特征和目标之间的生成关系，这也是为什么朴素贝叶斯分类器是生成模型的原因，然后利用贝叶斯公式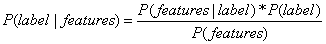
以及最大似然估计，估计出新样本最有可能的先验概率P(label)与P(features|label)的乘积，就可以得出最有可能的label。
（注：另一种方法是使用逻辑回归等其他算法直接对P(label|feature)建模，也就是直接学习出特征X和目标y之间的关系，这属于判别方法。）
整个推导过程如下：
根据贝叶斯定理：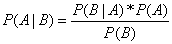
，我们把数据集的特征（features）和标签（label）代入其中得到： 。
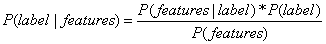由于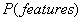
是常量（constant），该公式可改写成：
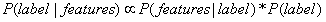。（∝表示成正比）
朴素贝叶斯假设各特征之间相互独立，于是就有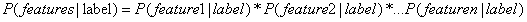
。（注：朴素贝叶斯之所以被称为“朴素”，就是因为它假设各个特征之间相互独立。）
此时，公式可写成：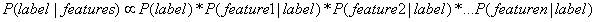
。
也即：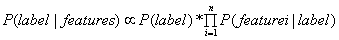
。
（注：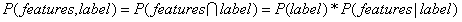
）
我们不想知道后验概率P(label|features)的分布，而是想知道最有可能的P(label|feature)，因此我们用极大似然估计法对条件概率P(features|label)和先验概率P(label)进行估计，然后得到对后验概率P(label|features)的最好估计：
。
也就是说，朴素贝叶斯分类器把样本分到后验概率P(label|featurees)最大的分类当中。
根据对数据集P(features|label)分布的不同假设，朴素贝叶斯分类器可分为不同的类型，以下是三种常见的类型：
1. 高斯朴素贝叶斯（Gaussian Naive Bayes） --- 假设特征是连续值，且符合高斯分布。单个特征条件概率的计算公式：
2. 多项式朴素贝叶斯（Multinomial Naive Bayes） --- 假设特征向量由多项分布生成。单个特征条件概率的计算公式：
3. 伯努利朴素贝叶斯（Bernoulli Naive Bayes） --- 假设特征是独立的布尔类型。单个特征条件概率的计算公式：
需要注意的是：某一特征可能在训练集中从未出现过，其条件概率P(xi|Ck)会变为0，这样就会导致后验概率也为0，这显然是不对的。此外，还有可能某个类别在训练集中从未出现，这样y的先验概率会变成0，同样会导致后验概率也为0。解决办法是引入拉普拉斯平滑（Laplace Smoothing），公式如下：
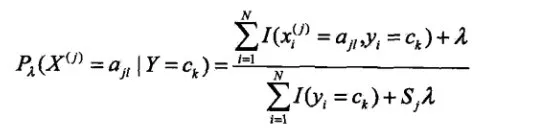
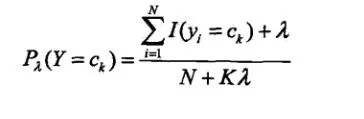
其中ajl代表第j个特征的第l个值，Sj代表第j个特征有哪几种选择，K代表类别总数。λ一般设为1。
加入拉普拉斯平滑之后，避免了出现概率为0的情况，在训练样本数足够多的情况下，也不会对结果产生很大影响。
贝叶斯分类器算法总结如下：
假设训练集特征数为i，记作xi，目标为k个类别，记为Ck，样本数为n，新样本特征记作xnew_sample。
1，计算出先验概率P(Ck)，即每个类别在训练集中的概率；
2，分别计算出训练集中每个特征在每个类别下的条件概率P(xi|Ck)，具体分为以下三种情况；
a）如果特征数据是离散值，那么我们假设其符合多项分布，代入公式
b）如果特征数据是布尔类型的离散值，那么我们假设其符合伯努利分布，代入公式
c）如果特征数据是连续值，那么我们假设其符合高斯分布。只需要求出这个特征在每个类别下的平均值μk和方差σk2，然后代入公式
3，对于需要预测类别的新样本，分别计算每个类别下的极大后验概率：
（我们在实际计算中为防止数据下溢，将连乘运算取对数变成相加运算）；
4，对上述极大后验概率进行比较，最大的那个对应的类别即为结果；
贝叶斯分类器的优点：1. 训练和预测的速度非常快（由于假设每个特征相互独立，因此每个条件概率P(feature|label)的分布可以独立地被一维分布估计出来）
2. 容易解释
3. 可调参数少
4. 尽管朴素贝叶斯模型对特征之间相互独立这一假设在实际应用中往往不成立，但其分类效果仍然不错
贝叶斯分类器缺点：1. 由于朴素贝叶斯分类器对数据分布有严格的假设，因此它的预测效果通常比复杂模型差
适用于：1. 各个类别的区分度很高
2. 维度非常高的数据集
3. 为分类问题提供快速粗糙的基本方案
经典应用：多项朴素贝叶斯和伯努利朴素贝叶斯常用于文档分类（document classification），垃圾邮件过滤（spam filtering）