一、树的基本概念
(1)树(Tree)的概念:树是一种递归定义的数据结构,是一种重要的非线性数据结构。
树可以是一棵空树,它没有任何的结点;也可以是一棵非空树,至少含有一个结点。
(2)根(Root):有且仅有一个结点的非空树,那个结点就是根。
(3)子树(Subtree):在一棵非空树中,除根外,其余所有结点可以分为m(m≥0)个互不相交的集合。每个集合本身又是一棵树,称为根的子树。
(4)结点(Node):表示树中的元素及若干指向其子树的分支。
(5)结点的度(Degree):一个结点拥有的子树数目称为该结点的度。
(6)叶子结点(Leaf):度为0的结点。
(7)孩子(Child):结点子树的根称为该结点的孩子。
(8)双亲(Parents):孩子结点的上层结点叫该结点的双亲。
(9)兄弟(Sibling):同一双亲的孩子。
(10)树的度:一棵树中最大的结点度数。
(11)结点的层次(Level):从根结点开始定义根为第一层,它的孩子为第二层,依此类推。
(12)深度(Depth):树中结点最大层次的值。
(13)有序树:树中的各子树自左向右有序的称为有序树。
(14)无序树:树中的各子树自左向右无序的称为无序树。
(15)森林(Forest):是m(m≥0)棵互不相交的树的集合。
(16)祖先:是指从根结点到该结点之间所有的结点。
如图所示:
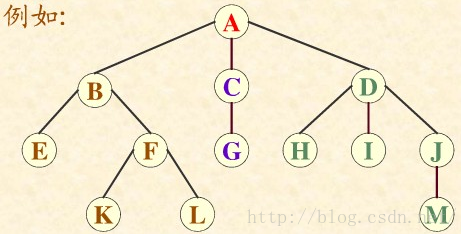
A是根结点,A结点的度是3,D结点的度是3;因为3是结点的度的最大值,所以这棵树的度是3;E、G、H、I、K、L和M是叶子结点。
A在树的第一层,B、C、D在树的第二层,E、F、G、H、I、J在树的第三层,K、L、M在树的第四层;树的深度是4。
树从左往右是有序的,这是一棵有序树;E结点的祖先是A、B。
二 二叉树
概念:二叉树又叫二分树,它的特点是每个结点最多只有二棵子树,也就是二叉树中没有度大于2的结点。二叉树的子树有左右之分,严格区分左孩子、右孩子,其次序不能颠倒。
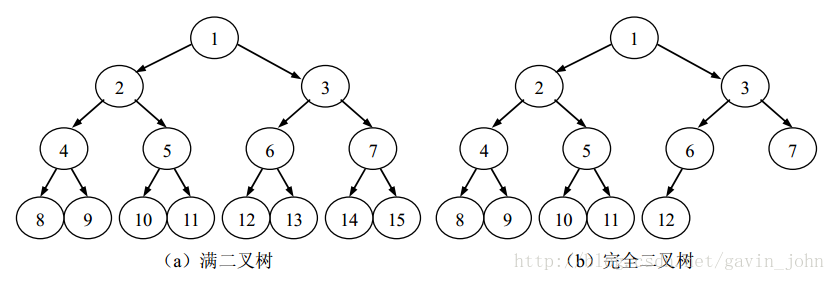
满二叉树
概念:一棵深度为k且有2k-1个结点的二叉树称为满二叉树。
完全二叉树
概念:可以对满二叉树的结点进行连续编号,约定编号从根结点起,自上而下,自左至右。由此可以引出完全二叉树的定义。深度为k的,有n个结点的二叉树,当且仅当其每一个结点都与深度为k的满二叉树中编号从1至n的结点一一对应,称之为完全二叉树。
完全二叉树的特点是:
(1)叶子结点只可能在层次最大的两层上出现;(2)对任一结点,若其右分支下的子孙的最大层次为l,则其左分支下的子孙的最大层次必为l或l+1。
三 性质
性质1: 在二叉树的第i层上至多有2i-1个结点(i>=1)
性质2: 深度为k的二叉树至多有2k-1个结点,(k>=1).

性质3: 对任何一棵二叉树T,如果其终端结点数位n0,度为2的结点数为n2,则 n0 = n2 + 1
性质4: 具有n个结点的完全二叉树的深度为 ⌊log2n⌋+1
性质5: 如果对一棵有n个结点的完全二叉树(其深度为 ⌊log2n⌋+1 )的结点按层序编号(从第1层到第 ⌊log2n⌋+1 层,每层从左到右),则对任一结点i(1<=i<=n),有:
(1)如果i=1,则结点i是二叉树的根,无双亲;如果i>1,则其双亲PARENT(i)是结点⌊i/2⌋。
(2)如果2i>n,则结点i无左孩子(结点i为叶子结点);否则其左孩子LCHILD(i)是结点2i。
(3)如果2i+1>n,则结点i无右孩子;否则其右孩子RCHILD(i)是结点2i+1。
四 python 代码
代码
class Node: "定义节点类" def __init__(self,item): self.item=item self.lchild=None self.rchild=None class Tree: "定义树类" def __init__(self): self.root=None def add(self,item): node=Node(item) if not self.root: self.root=node return queue=[self.root,] while queue: current_node=queue.pop(0) if current_node.lchild is None: current_node.lchild=node return else: queue.append(current_node.lchild) if current_node.rchild is None: current_node.rchild=node return else: queue.append(current_node.rchild) def breadth_travel(self): '''广度遍历''' if self.root is None: return queue=[self.root,] while queue: current_node=queue.pop(0) print(current_node.item,end=" ") if current_node.lchild is not None: queue.append(current_node.lchild) if current_node.rchild is not None: queue.append(current_node.rchild) def preorder(self,node): '''先序遍历----根->左->右''' if node is None: return print(node.item,end=" ") self.preorder(node.lchild) self.preorder(node.rchild) def inorder(self,node): '''中序遍历----左->中->右''' if node is None: return self.inorder(node.lchild) print(node.item,end=" ") self.inorder(node.rchild) def postorder(self,node): '''后序遍历----左->右->中''' if node is None: return self.postorder(node.lchild) self.postorder(node.rchild) print(node.item,end=" ") if __name__ == '__main__': tree=Tree() tree.add(0) tree.add(1) tree.add(2) tree.add(3) tree.add(4) tree.add(5) tree.add(6) tree.add(7) tree.add(8) tree.add(9) print('-----广度遍历-----') tree.breadth_travel() print(' -----深度先序遍历-----') tree.preorder(tree.root) print(' -----深度中序遍历-----') tree.inorder(tree.root) print(' -----深度后序遍历-----') tree.postorder(tree.root)
树形结构
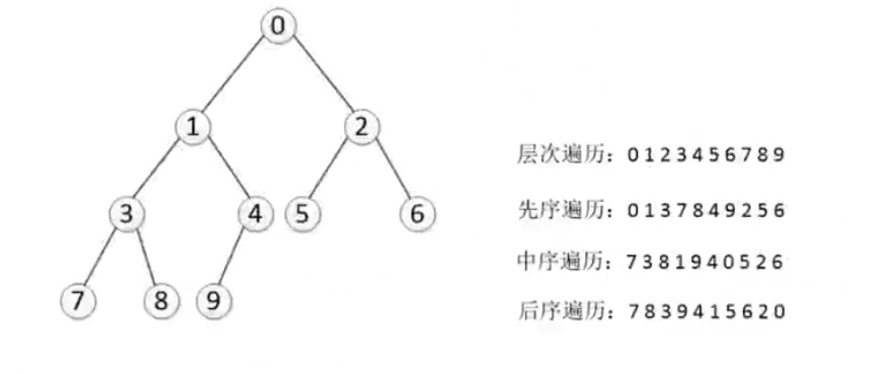
结果
-----广度遍历----- 0 1 2 3 4 5 6 7 8 9 -----深度先序遍历----- 0 1 3 7 8 4 9 2 5 6 -----深度中序遍历----- 7 3 8 1 9 4 0 5 2 6 -----深度后序遍历----- 7 8 3 9 4 1 5 6 2 0
好文推荐
原文:https://blog.csdn.net/tfygg/article/details/46763389
原文:https://blog.csdn.net/gavin_john/article/details/72312276