2680: 最大矩阵连乘次数 
Time Limit(Common/Java):1000MS/10000MS Memory Limit:65536KByte
Total Submit: 144 Accepted:77
Total Submit: 144 Accepted:77
Description
给定n个矩阵{A1,A2,…,An},其中Ai与Ai+1是可乘的,i=1,2 ,…,n-1。如何确定计算矩阵连乘积的计算次序,使得依此次序计算矩阵连乘积需要的数乘次数最大。
Input
输入包含多组测试数据。第一行为一个整数C,表示有C组测试数据,接下来有2*C行数据,每组测试数据占2行,每组测试数据第一行是1个整数n(n≤10),表示有n个矩阵连乘,接下来一行有n+1个数,表示是n个矩阵的行及第n个矩阵的列,它们之间用空格隔开。
Output
你的输出应该有C行,即每组测试数据的输出占一行,它是计算出的矩阵最大连乘积次数。
Sample Input
1
3
10 100 5 50
Sample Output
75000
Source
矩阵乘法满足结合律
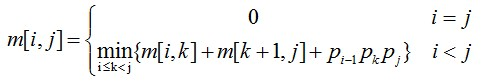
#include <stdio.h> int w,n,p[30],m[30][30],s[30][30]; int main() { scanf("%d",&w); while(w--) { scanf("%d",&n); for(int i=0; i<=n; i++) scanf("%d",&p[i]); for(int i=1; i<=n; i++) m[i][i]=0; for(int r=2; r<=n; r++) for(int i=1; i<=n-r+1; i++) { int j=r+i-1; m[i][j]=m[i+1][j]+p[i-1]*p[i]*p[j]; s[i][j]=i; for(int k=i+1; k<j; k++) { int t=m[i][k]+m[k+1][j]+p[i-1]*p[k]*p[j]; if(t>m[i][j]) { m[i][j]=t; s[i][j]=k; } } } printf("%d ",m[1][n]); } return 0; }