三门问题(Monty Hall problem)也称为蒙提霍尔问题或蒙提霍尔悖论,出自美国的电视游戏节目《Let’s Make a Deal》。问题名字来自该节目的主持人蒙提·霍尔(Monty Hall)。
这个游戏的玩法是:参赛者会看见三扇关闭的门,其中一扇门后面有一辆汽车,选中后面有车的那扇门就可以赢得该汽车,而另外两扇门后面则各藏有一只山羊。当参赛者选定了一扇门,但未去开启它的时候,节目主持人会开启剩下两扇门中的一扇,露出其中一只山羊。主持人其后会问参赛者要不要更换其初始的选择,选另一扇仍然关上的门。
那么问题来了,参赛者到底要不要更换其初始的选择呢?
解决这个问题需要用到贝叶斯定理: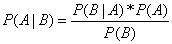
让我们选一个特定的例子来看看:假设三扇门分别为Door A,Door B,Door C,并且参赛者初始选定了Door A,然后主持人展示了Door B。那么参赛者是坚持选择Door A还是更换成Door C呢?这就要根据Door A和Door C哪个门后汽车出现的概率较大决定了。
也就是说,我们需要解决P(Door A=car|Door A is selected, Door B is revealed)和P(Door C=car|Door A is selected, Door B is revealed)哪个大的问题。
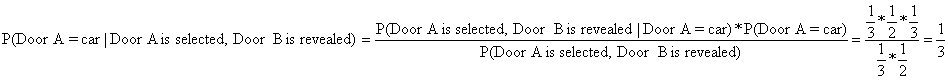

首先,每个门后有车的概率都是1/3: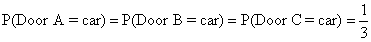
其次,如果Door A门后有汽车,那么Door A被选择的几率是1/3,假设初始选择了Door A,那么Door B被主持人打开的几率是1/2: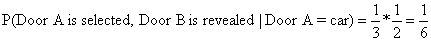
再次,普通情况下,Door A被选择的几率是1/3,Door B被主持人打开的几率是1/2(因为已经有一扇门被选择了,选择的门不能被打开):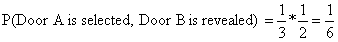
同理,如果Door C门后有汽车,那么Door A被选择的几率是1/3,假设初始选择了Door A,那么Door B被主持人打开的几率是1: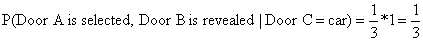
因此,我们可以看到,P(Door C=car|Door A is selected, Door B is revealed)是P(Door A=car|Door A is selected, Door B is revealed)的两倍。也就是说,更换初始的选择将会使我们的获胜几率提高2倍!
可以用probability tree来帮助理解一下:
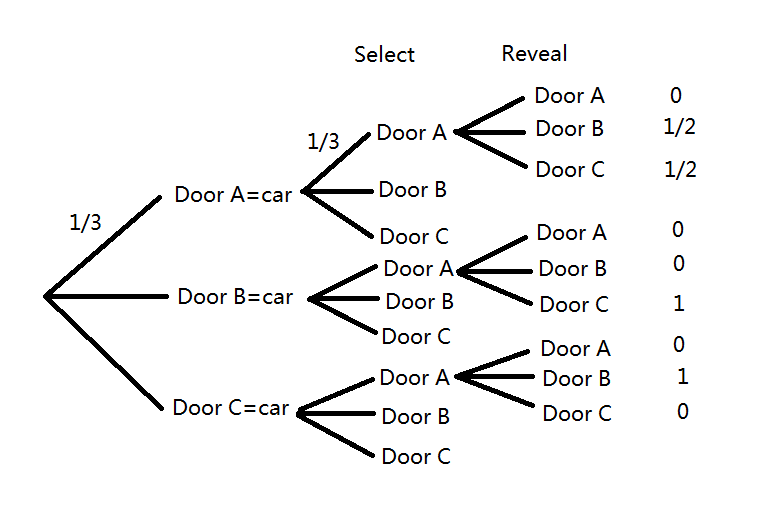
如果对上面的计算公式还有疑问,那么让我们用计算机来模拟一下:
from random import randint from random import choice N = 1000 def simulate(N): m=0 #设置不更换初始选择赢得汽车的次数 n=0 #设置更换初始选择赢得汽车的次数 for i in range(N): #模拟1000次游戏 win=randint(1,3) #设置藏有汽车的门,在1-3之间随机选出 bet1=randint(1,3) #设置初始选择的门,在1-3之间随机选出 remain=[i for i in range(1,4) if i!=win and i!=bet1] #剩余可选的门(除去初始选择的门和藏有汽车的门) monty_reveal=choice(remain) #monty会在剩余可选的门中选择一扇门打开 bet2=6-bet1-monty_reveal #bet2表示更换初始选择(用6减是因为三扇门加起来等于6) if bet1==win: #如果初始选择和藏有汽车的门吻合,那么初始选择的获胜次数+1 m+=1 if bet2==win: ##如果更换初始选择的bet2和藏有汽车的门吻合,那么bet2的获胜次数+1 n+=1 return n/m print(simulate(N))
2.0211480362537766
最后的结果: 更换初始选择获胜的次数差不多是不更换初始选择获胜次数的两倍。
三门问题是有些反直觉的,我们可以这样来理解:当参赛者选择Door A时,他的获胜概率是1/3,当主持人展示了Door B门后没有汽车以后,这个信息并没有给参赛者的初始选择带来任何有用的信息 ,选择Door A获胜的概率仍然是1/3,但是鉴于选择Door B获胜的概率降为了0,因此选择Door C获胜的概率变为1-1/3,也就是2/3。
参考:https://classroom.udacity.com/courses/st101/lessons/48744119/concepts/484806120923