这里用文氏图(Venn diagram)来推导一下贝叶斯定理。
假设A和B为两个不相互独立的事件。
交集(intersection): 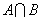
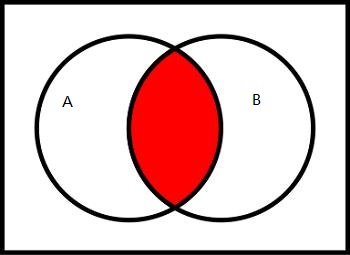
上图红色部分即为事件A和事件B的交集。
并集(union): 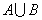
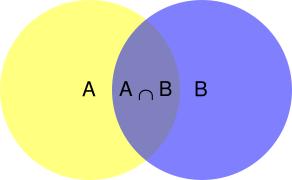
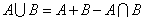
由Venn diagram可以看出,在事件B已经发生的情况下,事件A发生的概率为事件A和事件B的交集除以事件B:

同理,在事件A已经发生的情况下,事件B发生的概率为事件A和事件B的交集除以事件A:
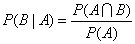
注: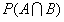 表示 A,B 事件同时发生的概率,如果 A 和 B 是相互独立的两个事件,那么:
表示 A,B 事件同时发生的概率,如果 A 和 B 是相互独立的两个事件,那么: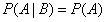 。
。
由上面的公式可以得到:
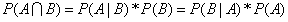
然后,我们就可以得到贝叶斯定理:
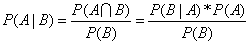
其中: 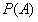 是先验概率(prior probability),
是先验概率(prior probability),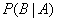 是条件概率(conditional probability),
是条件概率(conditional probability),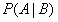 是后验概率(posterior probability)。
是后验概率(posterior probability)。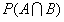 是联合概率(joint probability),通常写成P(A,B)。
是联合概率(joint probability),通常写成P(A,B)。
注:条件概率 P(B|A) ---> 给定事件A,事件B发生的概率(probability of event B occuring given event A)。
又根据Law of Total Probability: 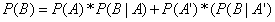
注: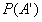 表示事件A不发生的概率。
表示事件A不发生的概率。
这个可以用probability tree来帮助理解一下:
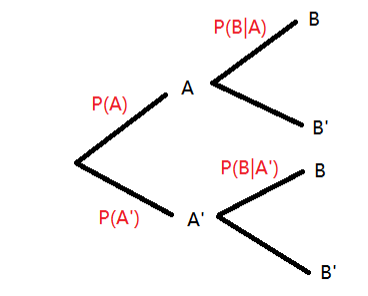
因此,贝叶斯定理可以扩展为: 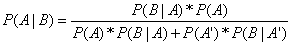
贝叶斯定理通常用于由已知的先验概率和条件概率,推算出后验概率。
举一个简单的例子:某地平时下雨的概率是0.3,小明平时带伞的概率是0.4,小明下雨天带伞的概率是0.8。某一天小明带了伞,请问这天下雨的概率是多少?
解答:也就是需要求P(下雨|小明带伞),把上面的数字代入公式即:
这个例子的先验概率是平时下雨的概率0.3,由于我们已知小明带了伞这一信息,因此我们可以估算出后验概率,也就是当天下雨的概率是0.6。
先验概率是怎么得来的呢?通常是人们的经验总结或者说是估算,比如说某地一个月里面下了3天雨,我们就估算某地平时下雨的概率是0.3。
如果条件不止一个呢?让我们把上面的例子改一下:某地平时下雨的概率是0.3,平时刮风的概率是0.4,下雨天刮风的概率是0.6,小明平时带伞的概率是0.4,小明下雨天带伞的概率是0.8。某一天小明带了伞,且当天在刮风,请问这天下雨的概率是多少?
解答:也就是需要求P(下雨|小明带伞,刮风),把上面的数字代入公式即:
![]()
注:这里假设小明带伞和刮风之间没有关联,两条件互不影响(条件独立假设),因此属于朴素贝叶斯的范畴。
长久以来,人们信奉的是频率主义。比如把一枚硬币抛10000次,有5000次正面朝上,5000次反面朝上,那么我们就可以得知抛这枚硬币,其正面朝上的概率是0.5。通常,我们需要某一事件发生足够多的次数,我们才可以观察到它的规律。
在现实生活中,很多事件并不会在相对较短的时间内多次发生。这时候,贝叶斯定理就发挥作用了。比如说我们想知道刮风天下雨的概率是多少,我们不用等10000个刮风天,看其中有几天下了雨。我们只需要估算出下雨天会刮风的概率,平时下雨的概率,平时刮风的概率,就可以估算出刮风天会下雨的概率是多少了。先验概率估算得不准确并没有关系,人们可以通过未来事件的发生情况,不断对后验概率做出调整。