在做分类时常常需要估算不同样本之间的相似性,通常采用的方法就是计算样本间的距离。
常用的有:
欧氏距离:源于欧式空间中两点的距离公式,np.outer(计算内积)
曼哈顿距离(城市街区距离)
切比雪夫距离:国际象棋
闵可夫斯基距离:闵氏距离不是一种距离,而是一组距离的定义
两个n维变量a(x11,x12,…,x1n)与 b(x21,x22,…,x2n)间的闵可夫斯基距离定义为:

其中p是一个变参数。
当p=1时,就是曼哈顿距离
当p=2时,就是欧氏距离
当p→∞时,就是切比雪夫距离
闵氏距离的缺点主要有两个:(1)将各个分量的量纲(scale),也就是“单位”当作相同的看待了。(2)没有考虑各个分量的分布(期望,方差等)可能是不同的。
比如:二维样本(身高,体重),其中身高范围是150~190,体重范围是50~60,有三个样本:a(180,50),b(190,50),c(180,60)。那么a与b之间的闵氏距离(无论是曼哈顿距离、欧氏距离或切比雪夫距离)等于a与c之间的闵氏距离,但是身高的10cm真的等价于体重的10kg么?因此用闵氏距离来衡量这些样本间的相似度很有问题,要先归一化~
标准欧式距离:将各个分量都“标准化”到均值、方差相等
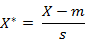
标准化后的值 = ( 标准化前的值 - 分量的均值 ) /分量的标准差
马氏距离:
有M个样本向量X1~Xm,协方差矩阵记为S,均值记为向量μ,则其中样本向量X到u的马氏距离表示为:
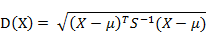
同理,向量Xi与Xj之间的马氏距离定义为:

若协方差矩阵是单位矩阵,马氏距离变成了欧氏距离
若协方差矩阵是对角矩阵,马氏距离就变成了标准化欧氏距离
*马氏距离的优缺点:量纲无关,排除变量之间的相关性的干扰
夹角余弦:夹角余弦越大表示两个向量的夹角越小,夹角余弦越小表示两向量的夹角越大
汉明距离:两个等长字符串s1与s2之间的汉明距离定义为将其中一个变为另外一个所需要作的最小替换次数
杰卡德相似系数:两个集合A和B的交集元素在A,B的并集中所占的比例
与杰卡德相似系数相反的杰卡德距离用两个集合中不同元素占所有元素的比例来衡量两个集合的区分度
相关系数:衡量随机变量X与Y相关程度的一种方法,相关系数的取值范围是[-1,1]。相关系数的绝对值越大,则表明X与Y相关度越高。当X与Y线性相关时,相关系数取值为1(正线性相关)或-1(负线性相关)。
参考博文:
1.http://www.cnblogs.com/heaad/archive/2011/03/08/1977733.html