Burst Balloons
Given n balloons, indexed from 0 to n-1. Each balloon is painted with a number on it represented by array nums. You are asked to burst all the balloons. If the you burst balloon i you will get nums[left] * nums[i] * nums[right] coins. Here left and right are adjacent indices of i. After the burst, the left and right then becomes adjacent.
Find the maximum coins you can collect by bursting the balloons wisely.
Note:
(1) You may imagine nums[-1] = nums[n] = 1. They are not real therefore you can not burst them.
(2) 0 ≤ n ≤ 500, 0 ≤ nums[i] ≤ 100
Example:
Given [3, 1, 5, 8]
Return 167
nums = [3,1,5,8] --> [3,5,8] --> [3,8] --> [8] --> [] coins = 3*1*5 + 3*5*8 + 1*3*8 + 1*8*1 = 167
https://leetcode.com/problems/burst-balloons/
分治+动态规划。
https://leetcode.com/discuss/72216/share-some-analysis-and-explanations
先是暴力的思路,n个气球一个个踩,剩下n - 1个再按顺序踩,一直到最后,复杂度爆表TLE。
加入分治的思想,踩了一个气球后,数组就分成左右两部分,但问题是左边和右边不是独立的,这样分治结果是错的。
逆向思考,最后只有一个气球的时候,结果的是肯定的,因为这个气球的左右分别是左边界和右边界。
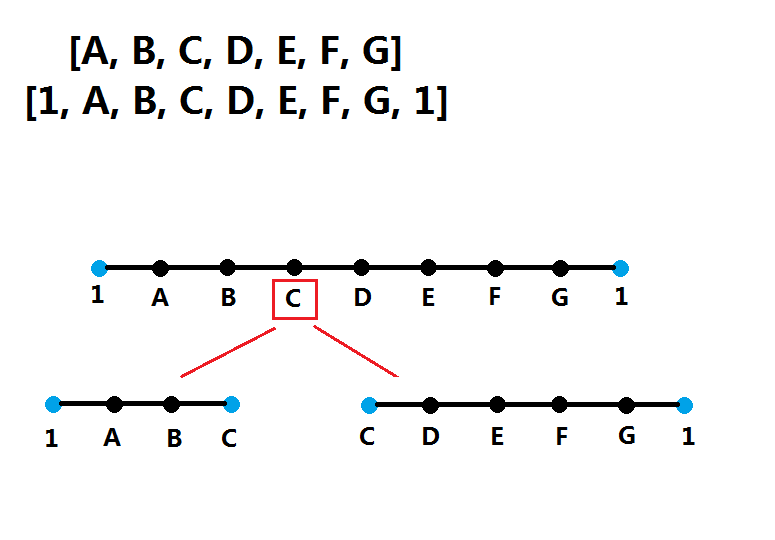
举例来说,数组[A,B,C,D,E,F,G],代表任意数字。
首先去掉所有的零,在头和尾加上两个1表示边界。
最外层循环就是从A到G,代表了最后一个踩的气球。
假设遍历到C这个点,最后要踩C,那么C的值是固定的,为1 * C * 1。
然后考虑两边,左边的是以1和C为边界,求出最大值,右边是以C和1为边界求最大值,如图所示。
递归求出结果。
还要开一个二维数组记录中间结果提高效率。
1 /**
2 * @param {number[]} nums
3 * @return {number}
4 */
5 var maxCoins = function(nums) {
6 var dp = [], i, numArr = [1];
7 for(i = 0; i <nums.length; i++){
8 if(nums[i] !== 0) numArr.push(nums[i]);
9 }
10 numArr.push(1);
11 var len = numArr.length;
12 for(i = 0; i < len; i++){
13 dp[i] = [];
14 }
15 return burstBalloons(1, len - 2);
16
17 function burstBalloons(start, end){
18 if(start > end) return 0;
19 if(dp[start][end]) return dp[start][end];
20 var max = -Infinity;
21 for(var i = start; i <= end; i++){
22 max = Math.max(max, numArr[start - 1] * numArr[i] * numArr[end + 1] +
23 burstBalloons(start, i - 1) + burstBalloons(i + 1, end));
24 }
25 dp[start][end] = max;
26 return max;
27 }
28 };
