BZOJ 1832
写起来很放松的题。
首先发现三个点在树上一共只有$3$种形态,大概长这样:
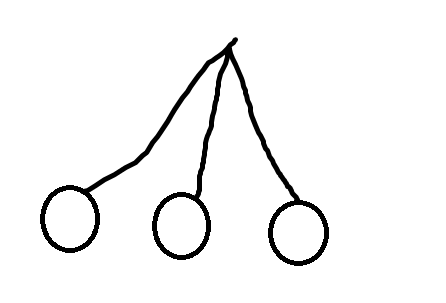
这种情况下显然走到三个点的$lca$最优。

这种情况下走到中间那个点最优。
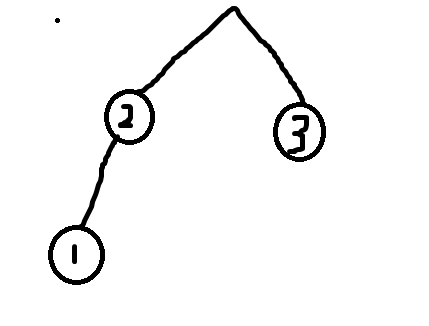
这种情况下走到$2$最优。
有趣的事情来了:我们发现树上的三个点,会有三个$lca$,而当两个$lca$相同时,另外一个$lca$就成了最优解。
考虑一下怎么计算路程,只要分别算算三个图就会发现最后路程的式子也是统一的,(假设点为$x, y, z$)就是$dep_x + dep_y + dep_z - dep_{lca(x, y)} - dep_{lca(y, z)} - dep_{lca(x, z)}$。
时间复杂度$O(nlogn)$。
感觉倍增挺卡的,但是$2 * n = 1e6$完全不敢$rmq$啊$233$,链剖应该是比较优秀的做法吧。
Code:

#include <cstdio> #include <cstring> using namespace std; const int N = 5e5 + 5; const int Lg = 22; int n, qn, tot = 0, head[N], dep[N], fa[N][Lg]; struct Edge { int to, nxt; } e[N << 1]; inline void add(int from, int to) { e[++tot].to = to; e[tot].nxt = head[from]; head[from] = tot; } inline void swap(int &x, int &y) { int t = x; x = y; y = t; } inline void read(int &X) { X = 0; char ch = 0; int op = 1; for(; ch > '9'|| ch < '0'; ch = getchar()) if(ch == '-') op = -1; for(; ch >= '0' && ch <= '9'; ch = getchar()) X = (X << 3) + (X << 1) + ch - 48; X *= op; } void dfs(int x, int fat, int depth) { fa[x][0] = fat, dep[x] = depth; for(int i = 1; i <= 20; i++) fa[x][i] = fa[fa[x][i - 1]][i - 1]; for(int i = head[x]; i; i = e[i].nxt) { int y = e[i].to; if(y == fat) continue; dfs(y, x, depth + 1); } } inline int getLca(int x, int y) { if(dep[x] < dep[y]) swap(x, y); for(int i = 20; i >= 0; i--) if(dep[fa[x][i]] >= dep[y]) x = fa[x][i]; if(x == y) return x; for(int i = 20; i >= 0; i--) if(fa[x][i] != fa[y][i]) x = fa[x][i], y = fa[y][i]; return fa[x][0]; } int main() { read(n), read(qn); for(int x, y, i = 1; i < n; i++) { read(x), read(y); add(x, y), add(y, x); } dfs(1, 0, 1); for(int x, y, z; qn--; ) { read(x), read(y), read(z); int xy = getLca(x, y), yz = getLca(y, z), xz = getLca(x, z), res; if(xy == yz) res = xz; else if(xy == xz) res = yz; else if(yz == xz) res = xy; printf("%d %d ", res, dep[x] + dep[y] + dep[z] - dep[xy] - dep[yz] - dep[xz]); } return 0; }
