当数组基本有序时,插入排序法效率很高,而希尔排序法就是充分利用插入排序法这一特长的高速算法。希尔排序法中,程序会重复进行以间隔为g的元素为对象的插入排序。
设g的集合为G,集合G中的数一般是降序排列,最后一个数必须为1。具体流程如下:
- 对集合G中的每一个g,执行如下操作:
- 将数组中以g为间隔的数使用插入排序法进行排序
以数组{4, 8, 9, 1, 10, 6, 2, 5, 3, 7}进行G={4, 3, 1}为例使用希尔排序,过程如下图所示:
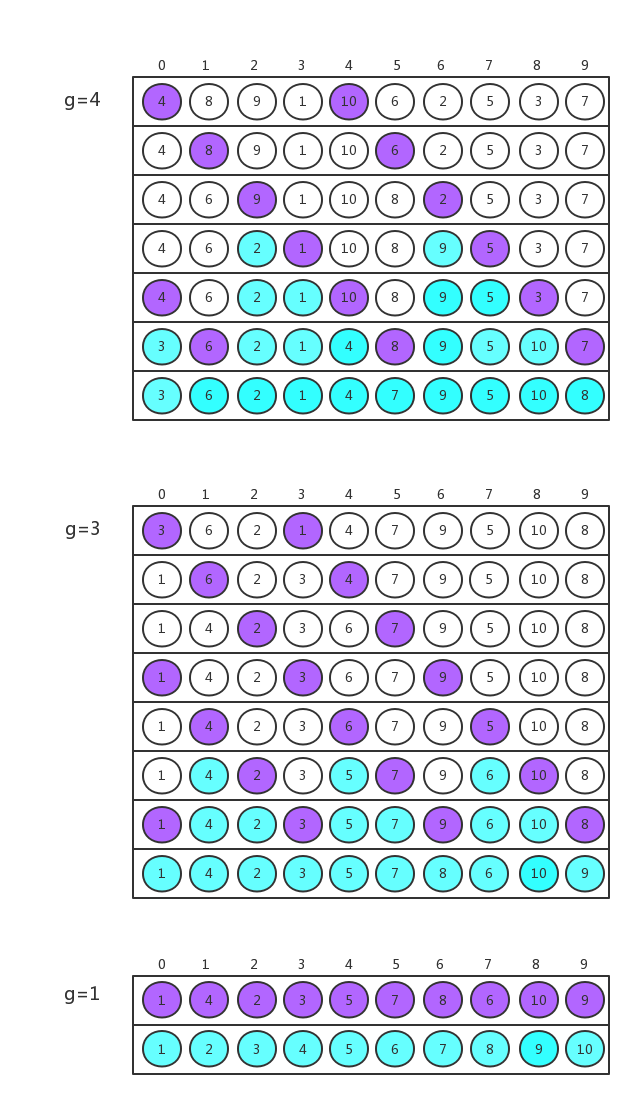
图中的紫色表示每次要排序的序列,蓝色表示在一次间隔中确定位置的数。要注意的一点是,程序的处理顺序与组的顺序无关。
g的选择方法很多,例如:当g=1, 4, 13, 40···即(g_{n+1}=3*g_{n}+1)时,算法的时间复杂度基本在(O(N^{1.25}))。
参考代码如下:
import java.util.ArrayList;
import java.util.List;
//希尔排序
//插入排序法可以高速处理顺序较整齐的数据,而希尔排序法就是充分发挥插入排序法这一特长的高速算法。
public static void shellSort(int[] num){
if (num==null || num.length==0)
return;
//生成数组G,表示间隔。因为G的大小不能确定,所以使用list
List<Integer> G = new ArrayList<>();
int h = 1;
while (h<num.length){
G.add(h);
h = 3*h + 1;
}
for (int i=G.size()-1; i>=0; i--){
insertionSortShell(num, G.get(i));
}
}
public static void insertionSortShell(int[] num, int g){
for (int i=g; i<num.length; i++){
int temp = num[i];
int j = i-g;
while (j>=0 && num[j]>temp){
num[j+g] = num[j];
j -= g;
}
num[j+g] = temp;
}
}
希尔排序不是稳定排序,时间复杂度也因g的选取和数组序列的顺序的不同而不同。