解题报告:
首先这题相当于数字三角形。
相当于从(0,5)出发,求到达底端的最大值
(i, 0) , (i, 10)这两个端点是要注意的,因为(i,0)只能到达(i+1, 0) 和 (i+1, 1), 而(i, 10)只能到达(i+1, 9), (i+1, 10)
#include <stdio.h> #include <string.h> #define MAXN 100010 int dp[MAXN][12]; int max_num(int a, int b, int c){ a = a > b ? a : b; a = a > c ? a : c; return a; } int main(){ int n, m, i, j, x, t; while(scanf("%d", &n) == 1 && n){ memset(dp, 0, sizeof(dp)); m = 0; for(i=0; i<n; i++){ scanf("%d %d", &x, &t); dp[t][x]++; if(m < t) m = t; } for(i=m-1; i>=0; i--){ dp[i][0] += dp[i+1][0] > dp[i+1][1] ? dp[i+1][0] : dp[i+1][1]; for(j=1; j<=10; j++){ dp[i][j] += max_num(dp[i+1][j-1], dp[i+1][j], dp[i+1][j+1]); } } printf("%d\n", dp[0][5]); } return 0; }
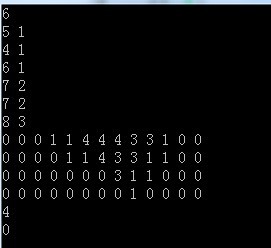
如果将题目给出的数据
6
5 1
4 1
6 1
7 2
7 2
8 3
0
输出dp便能轻易看出其中的道理