刷题篇--热题HOT 11-20

20.有效的括号

 给定一个只包括 '('，')'，'{'，'}'，'['，']' 的字符串，判断字符串是否有效。有效字符串需满足：
 左括号必须用相同类型的右括号闭合。
 左括号必须以正确的顺序闭合。
注意空字符串可被认为是有效字符串。
输入: "()"，输出: true；输入: "()[]{}"，输出: true；输入: "(]"，输出: false；输入: "([)]"，输出: false；输入: "{[]}"，输出: true；
分析：第一反应是使用栈，遇到左括号压入，遇到右括号弹出并比较.

class Solution {
    public boolean isValid(String s) {
        if(s.length()%2==1) return false;
        Stack<Character> brackets = new Stack();
        Map<Character,Character> map = new HashMap();
        map.put(')', '(');
        map.put(']', '[');
        map.put('}', '{');
        int countOfLeft=0,countOfRight=0;//计算左括号和右括号数量
        char[] chs = s.toCharArray();
        for(int i=0; i < chs.length; i++){
            if(chs[i] == '(' || chs[i] == '[' || chs[i] == '{'){
                countOfLeft++;
                brackets.push(chs[i]);
            }else if(chs[i] == ')' || chs[i] == ']' || chs[i] == '}'){
                countOfRight++;
                if(brackets.empty() || brackets.pop()!=map.get(chs[i])) return false;//如果括号栈为空或者弹出的不是正确左括号，则false
            }
        }
        return countOfLeft==countOfRight;//如果左括号数和右括号数量不相等则false
    }
}

21.合并两个有序链表

将两个有序链表合并为一个新的有序链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。
示例：输入：1->2->4, 1->3->4.输出：1->1->2->3->4->4。

 分析：新建头节点（解决链表问题需要注意这个小Tips）

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) { val = x; }
 * }
 */
class Solution {
    public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
        ListNode preNode = new ListNode(-1);
        ListNode resNode = preNode;
        while(l1 != null && l2 != null){
            if(l1.val > l2.val){
                preNode.next = l2;
                l2 = l2.next;
            }else{
                preNode.next = l1;
                l1 = l1.next;
            }
            preNode = preNode.next;
        }
        preNode.next = l1==null ? l2 : l1;
        return resNode.next;
    }
}

 22.括号生成

给出 n 代表生成括号的对数，请你写出一个函数，使其能够生成所有可能的并且有效的括号组合。

 例如，给出 n = 3，生成结果为：
[
  "((()))",
  "(()())",
  "(())()",
  "()(())",
  "()()()"
]

分析：n是括号的对数，即有n个左括号和n个右括号，当从前往后添加括号字符时，需要注意右括号的数量不能比左括号多，例如 （））…（因此第一个加入的肯定是左括号)，并且左括号的数量不能超过n个。

　　综上：添加括号字符时，只要保证左括号数目小于等于n，右括号数目小于等于左括号数目这两个条件就可以了。(从0开始计数)

class Solution {
    List<String> list = new ArrayList();
    public List<String> generateParenthesis(int n) {
        String s = "";
        int numOfLeft = 0, numOfRight = 0;
        addParenthesis(n, s, numOfLeft, numOfRight);
        return list;
    }
    public void addParenthesis(int n, String s, int numOfLeft, int numOfRight){
        //递归结束条件
        if(s.length() == 2*n){
            list.add(s);
            return;
        }
        if(numOfLeft < n){
            addParenthesis(n, s+'(', numOfLeft+1, numOfRight);
        }
        if(numOfRight < numOfLeft){
            addParenthesis(n, s+')', numOfLeft, numOfRight+1);
        }
    }
}

 23.合并K个排序列表

合并 k 个排序链表，返回合并后的排序链表。请分析和描述算法的复杂度。

 输入: [   1->4->5,   1->3->4,   2->6 ] 输出: 1->1->2->3->4->4->5->6

分析：21题我们做过合并两个链表，这里是合并K个链表，如何将两个联系起来？可以想到将第一个链表和第K个链表合并，第二个链表和第K-1个链表合并，一轮之后只剩下K/2个，再次执行此操作，直至K=1。时间复杂度：O(NK)

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) { val = x; }
 * }
 */
class Solution {
    public ListNode mergeKLists(ListNode[] lists) {
        int k = lists.length;
        if(k == 0) return null;
        while(k > 1){
            for(int i=0; i < k/2; i++){
                lists[i] = merge2Lists(lists[i], lists[k-1-i]);
            }
            k = (k+1)/2;
        }
        return lists[0];
    }
    public ListNode merge2Lists(ListNode l1, ListNode l2){
        ListNode newPre = new ListNode(-1);
        ListNode res = newPre;
        while(l1 != null && l2 != null){
            if(l1.val > l2.val){
                newPre.next = l2;
                l2 = l2.next;
            }else{
                newPre.next = l1;
                l1 = l1.next;
            }
            newPre = newPre.next;
        }
        newPre.next = l1 == null ? l2 : l1;
        return res.next;
    }
}

31.下一个排列

实现获取下一个排列的函数，算法需要将给定数字序列重新排列成字典序中下一个更大的排列。如果不存在下一个更大的排列，则将数字重新排列成最小的排列（即升序排列）。必须原地修改，只允许使用额外常数空间。
以下是一些例子，输入位于左侧列，其相应输出位于右侧列。
1,2,3 → 1,3,2
3,2,1 → 1,2,3
1,1,5 → 1,5,1

分析：下一个更大的排列：即从后往前找，看看后面有没有比前边一个数大的，如果有，则排列成最小数列。如果遍历完整个数组都没有找到符合条件的，则该数组是一个降序数组，此时应该考虑将数组转换成升序数组。

nums = [1,5,6,4,7,6,5,3,1]  => 当判决到 4和7 时，发生改变，需要将4和4后面与4差值（比4大）最小的数5交换位置，即分成1，5，6，5和7，6，4，3，1两个部分，前一部分保证比之前数列值大，后一部分保证仅比之前数列大一点点（保证"下一个"）。因此对后一部分还要进行升序排序。

class Solution {
    public void nextPermutation(int[] nums) {
        int len = nums.length;
        //找更大排列分界点
        int i = len-1;
        while(i>0 && nums[i]<=nums[i-1]){////如果跳出循环，即nums[i-1]比nums[i]小，4<7，i-1即是4的索引
            i--;
        }
        i = i-1;//i为分界点，即4的索引,如果i=-1表示没有，即原数组是一个升序数组
        if(i>=0){
            int j = len-1;
            while(j > i && nums[j] <= nums[i]){
                j--;//找出5的位置索引
            }
            swap(i,j,nums);//将4和5交换位置
        }
        //将4之后的数列降序处理或者整个数列进行降序处理
        //如果执行到此步说明没有更大数列，该数列为降序，现要改成升序
        reverse(nums, i+1);
    }
    public void reverse(int[] nums, int start){
        int i = start, j = nums.length-1;
        while(i<j){
            swap(i, j, nums);
            i++;
            j--;
        }
    }
    public void swap(int i, int j, int[] nums){
        int tmp = nums[i];
        nums[i] = nums[j];
        nums[j] = tmp;
    }
}

32.最长有效括号

给定一个只包含 '(' 和 ')' 的字符串，找出最长的包含有效括号的子串的长度。输入: "(()" 输出: 2 解释: 最长有效括号子串为 "()"；输入: ")()())" 输出: 4 解释: 最长有效括号子串为 "()()"

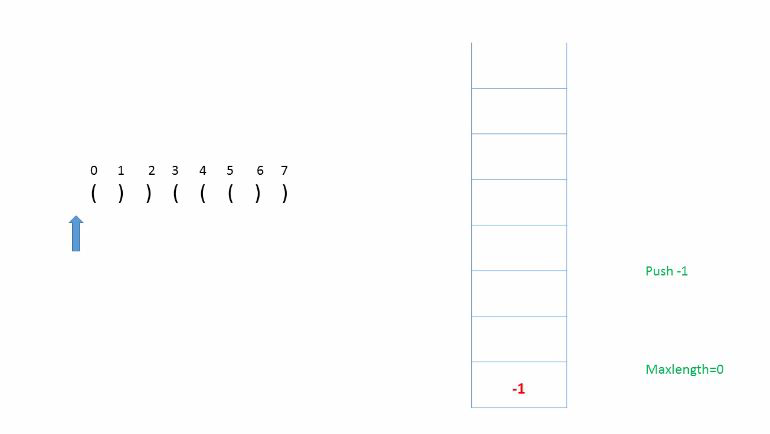
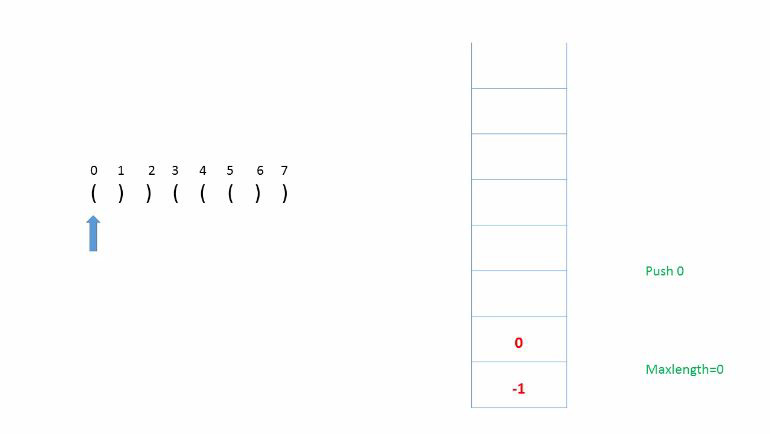
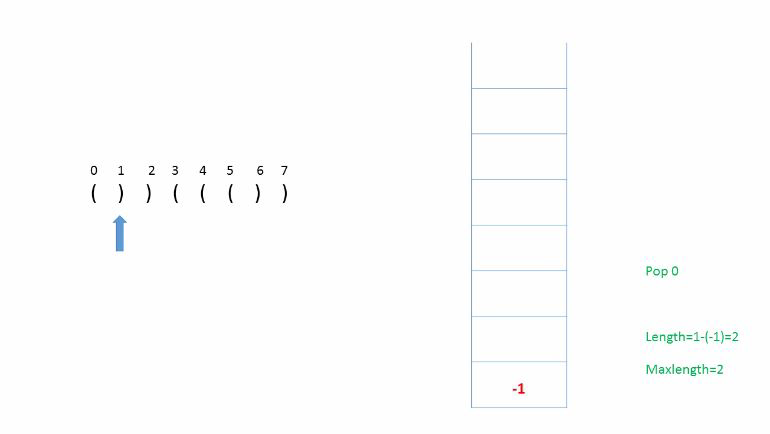
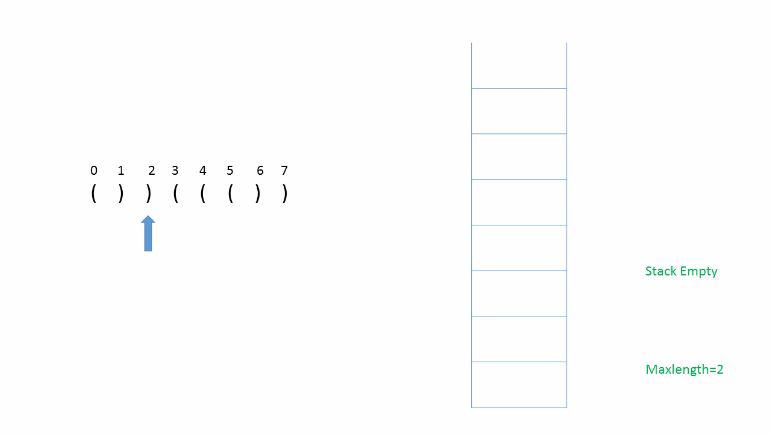
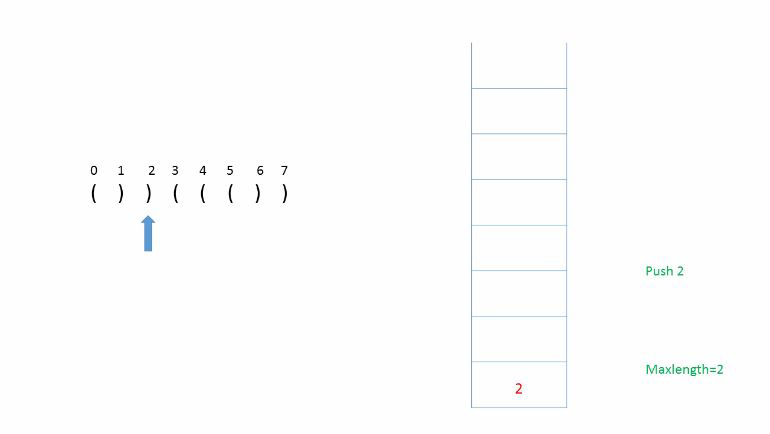
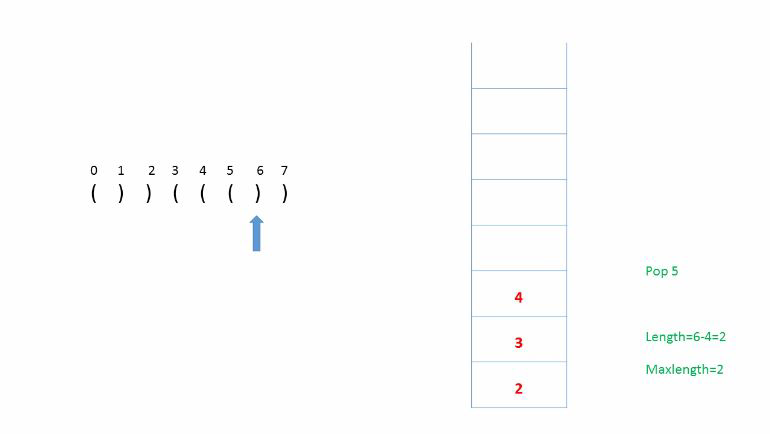
分析：使用栈，利用字符在字符串中的索引来计算最大长度。

例如 ：首先压入-1（便于计算最大长度），

　　　 遇到‘（’就压入索引，

　　　 遇到‘）’就弹出，

　　　  　如果弹出后栈不为空则当前最大长度为（当前索引-栈顶元素），并与总最大长度比较。

　　　  　如果弹出之后栈为空，说明之前的都弹完了，则压入当前索引，作为计算下一次最大长度初始值使用。

=》

=》

=》

=》

class Solution {
    public int longestValidParentheses(String s) {
        Stack<Integer> stack = new Stack();
        stack.push(-1);
        int maxLen = 0;
        for(int i=0; i<s.length(); i++){
            if(s.charAt(i) == '('){
                stack.push(i);
            }else{
                stack.pop();
                if(stack.empty()){
                    stack.push(i);
                }else{
                    maxLen = Math.max(maxLen, i-stack.peek());
                }
            }
        }
        return maxLen;
    }
}

33.搜索旋转排序数组

假设按照升序排序的数组在预先未知的某个点上进行了旋转。( 例如，数组 [0,1,2,4,5,6,7] 可能变为 [4,5,6,7,0,1,2] )。搜索一个给定的目标值，如果数组中存在这个目标值，则返回它的索引，否则返回 -1 。你可以假设数组中不存在重复的元素。你的算法时间复杂度必须是 O(log n) 级别。

示例 1:输入: nums = [4,5,6,7,0,1,2], target = 0输出: 4
示例 2:输入: nums = [4,5,6,7,0,1,2], target = 3输出: -1

分析：由题目中给出的复杂度可以得知使用二分查找，不断缩小查找范围。通过半段有序部分来划分（也可以先二分查找分界点，然后通过分界点来划分，但是要进行两次二分查找，较为麻烦）。

　　如果nums[start] <= nums[mid]， 例如 2，3，4，5，6，7，0，1    2<5，则说明start~mid的元素是有序的

　　　　如果nums[start] < target < nums[mid]，就在start~mid这个范围找，反之，则在后半部分查找。

　　如果nums[start] >= nums[mid]， 例如 5，6，7，1，2，3，4，   5>1，则说明mid~end的元素是有序的

　　　　如果nums[mid] < target < nums[end]，就在mid~end这个范围找，反之，则在前半部分查找。

class Solution {
    public int search(int[] nums, int target) {
        int start =0, end = nums.length-1;
        int mid;
        while(start <= end){
            mid = (start+end)/2;
            if(nums[mid]==target) return mid;
            if(nums[start] <= nums[mid]){
                if(nums[start] <= target && target < nums[mid]){
                    end = mid - 1;
                }else{
                    start = mid + 1;
                }
            }else{
                if(nums[mid] < target && target <= nums[end]){
                    start = mid +1;
                }else{
                    end = mid-1;
                }
            }
        }
        return -1;
    }
}

34.在排序数组中查找元素的第一个和最后一个位置

给定一个按照升序排列的整数数组 nums，和一个目标值 target。找出给定目标值在数组中的开始位置和结束位置。你的算法时间复杂度必须是 O(log n) 级别。如果数组中不存在目标值，返回 [-1, -1]。

示例 1:输入: nums = [5,7,7,8,8,10], target = 8 输出: [3,4]

示例 2:输入: nums = [5,7,7,8,8,10], target = 6 输出: [-1,-1]

分析：初始值left = 0, right = len-1，mid = （left + right）/2。target与mid比较。因为本题不只是找一个，则需要分别查找左边索引和右边索引，编写两个函数。

class Solution {
    public int[] searchRange(int[] nums, int target) {
        return new int[]{searchLeft(nums, target), searchRight(nums, target)};
    }
    //获取左边索引
    public int searchLeft(int[] nums, int target){
        int left = 0, right = nums.length-1, mid;
        while(left <= right){
            mid = (left + right)/2;
            if(nums[mid] == target){//当mid位置值等于目标值时
                if(mid==0 || nums[mid-1] != target){//判断是否再向前进一步查询
                    return mid;
                }else{
                    right = mid-1;//此时通过上面判断，mid-1位置依然等于target，因此进一步向左查询
                }
            }else if(nums[mid] > target ){
                right = mid - 1;
            }else{
                left = mid + 1;
            }
        }
        return -1;
    }
    //获取右边索引
    public int searchRight(int[] nums, int target){
        int left = 0, right = nums.length-1, mid;
        while(left <= right){
            mid = (left + right)/2;
            if(nums[mid] == target){//当mid位置值等于目标值时
                if(mid==nums.length-1 || nums[mid+1] != target){//判断是否再向前进一步查询
                    return mid;
                }else{
                    left = mid+1;//此时通过上面判断，mid+1位置依然等于target，因此进一步向右查询
                }
            }else if(nums[mid] > target ){
                right = mid - 1;
            }else{
                left = mid + 1;
            }
        }
        return -1;
    }
}

39.组合总和

给定一个无重复元素的数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。candidates 中的数字可以无限制重复被选取。所有数字（包括 target）都是正整数。解集不能包含重复的组合。

示例 1:输入: candidates = [2,3,6,7], target = 7,所求解集为:[ [7], [2,2,3]]
示例 2:输入: candidates = [2,3,5], target = 8,所求解集为:[  [2,2,2,2], [2,3,3], [3,5]]

分析：排列组合，类似于剑指Offer里字符串排列。

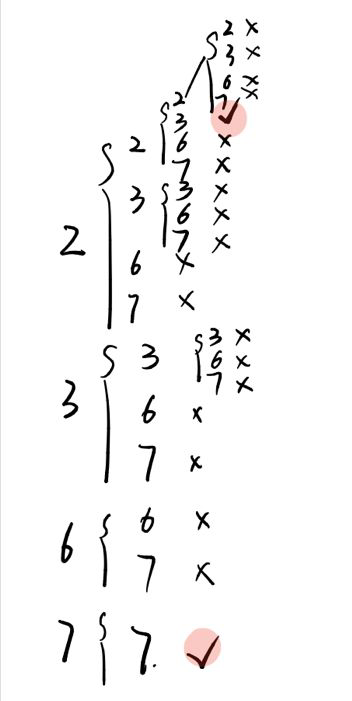
class Solution {
    List<List<Integer>> res = new ArrayList();
    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        Arrays.sort(candidates);//排序，方便去重
        List<Integer> list = new ArrayList();
        findCombination(candidates, target, 0, list);
        return res;
    }
    public void findCombination(int[] candidates, int target, int index, List<Integer> list){
        if(target < 0){
            return;
        } 
        if(target == 0){
            res.add(new ArrayList(list));
            return;
        }
        for(int i=index; i<candidates.length; i++){
            list.add(candidates[i]);
            findCombination(candidates, target-candidates[i], i, list);
            list.remove(list.size()-1);
        }
    }
}

 42.接雨水

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

 

上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。 感谢 Marcos 贡献此图。

示例:输入: [0,1,0,2,1,0,1,3,2,1,2,1]输出: 6

分析：当前柱子的接水量等于（min{左边最高柱子高度，右边最高柱子高度} - 当前高度），问题的关键就是如何找到并存储左右最高柱子高度值。

方法一：暴力寻找，每次遍历i时，再次遍历i左边，寻找左边最高柱子，然后再次遍历右边，寻找右边最高柱子。循环嵌套，时间复杂度O(N^2) 空间复杂度 O(1)

方法二：先从左往右遍历，使用数组存储左边最高值，再从右往左遍历，使用数组存储右边最高值。再从左往右遍历，计算接水量。时间复杂度O(N) 空间复杂度 O(N)。

class Solution {
    public int trap(int[] height) {
        int len = height.length, res = 0;
        if(len == 0) return 0;
        //左边最高块
        int[] maxLeft = new int[len];
        maxLeft[0] = height[0];
        for(int i = 1; i < len; i++){
            maxLeft[i] = Math.max(maxLeft[i-1], height[i]);
        }

        //右边最高块
        int[] maxRight = new int[len];
        maxRight[len-1] = height[len-1];
        for(int i = len-2; i >= 0; i--){
            maxRight[i] = Math.max(maxRight[i+1], height[i]);
        }

        //计算res
        for(int i = 0; i < len; i++){
            res += Math.min(maxLeft[i], maxRight[i]) - height[i];
        }

        return res;
        
    }
}

方法三：双指针法，通过分析可以知道以最高块为分界线（i=7），左边（0~6）接水量由左边最高值决定，右边（7~11）接水量由右边最高值决定.

那么如何在遍历中区分当前位置在左边还是右边呢？此时使用双指针，默认右边边界持有最高值，则当height[left] >= height[right]时，right指针就要向左移动，寻找比height[left]更大的值，反之，left指针向右移动，这个过程中双指针不断地向最高柱子移动，如果一个已经先到了，则会停止。时间复杂度O(N) 空间复杂度 O(1)

　　具体步骤如下：

　　while left < right

　　　　if height[left] < height[right]

　　　　　　if height[left] >= maxLeft

　　　　　　　　maxLeft = height[left]   //更新左边最大值

　　　　　　else

　　　　　　　　res +=  maxLeft - height[left]  //计算结果

　　　　　　left++

　　　　else

　　　　　　if height[right] >= maxright

　　　　　　　　maxright = height[right]   //更新右边最大值

　　　　　　else

　　　　　　　　res +=  maxLeft - height[left]  //计算结果

　　　　　　right --

class Solution {
    public int trap(int[] height) {
        int left = 0, right = height.length-1, maxLeft = 0, maxRight = 0, res = 0;
        while(left < right){
            if(height[left] < height[right]){
                if(height[left] >= maxLeft){
                    maxLeft = height[left];
                }else{
                    res += maxLeft - height[left];
                }
                left++;
            }else{
                if(height[right] >= maxRight){
                    maxRight = height[right];
                }else{
                    res += maxRight - height[right];
                }
                right--;
            } 
        }
        return res;
    }
}