正则化为什么可以防止过拟合
一个不一定正确的观点:
过拟合本质上是模型对于离群值过度敏感,最终拟合的函数过度拟合离群值。以下图为例,我们期望得到的拟合函数为黑色直线,而过拟合则会得到红色曲线。
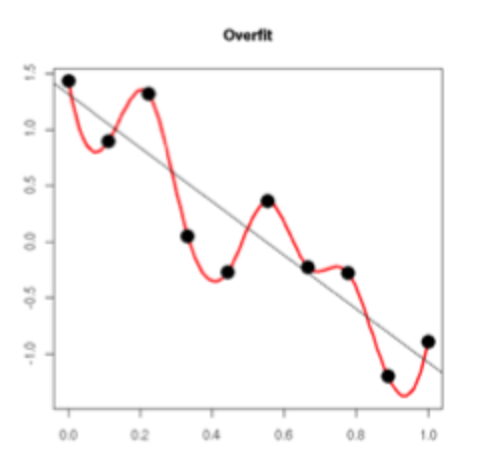
可以看出,过拟合函数在某些点波动很大,这里的波动大是因为离群值与正常值相差很大。一个函数波动大,反映到其导数上就是导数的范数很大。那么,通过抑制参数的范数大小,就能够避免函数过大的波动。我们以线性回归的正则化代价函数为例
[J( heta) = frac{1}{2m}sum_{i=1}^m(h_ heta(x^{(i)})-y^{(i)})^2 + frac{lambda}{2m}sum_{j=1}^n heta_j^2
]
假设(0 < lambda_1 < lambda_2)最终都训练出(J( heta) = d)的模型,由刚才的分析,(lambda_2)对应的( heta_2)的范数必须相对于( heta_1)的范数更小,才能够得到(J( heta_2) = J( heta_1) = d)
这就是正则项能防止过拟合的原理