1074. Number of Submatrices That Sum to Target (H)

Number of Submatrices That Sum to Target (H)

题目

Given a matrix and a target, return the number of non-empty submatrices that sum to target.

A submatrix x1, y1, x2, y2 is the set of all cells matrix[x][y] with x1 <= x <= x2 and y1 <= y <= y2.

Two submatrices (x1, y1, x2, y2) and (x1', y1', x2', y2') are different if they have some coordinate that is different: for example, if x1 != x1'.

Example 1:

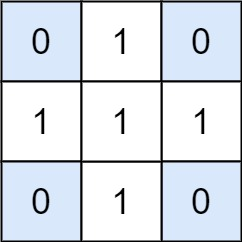
Input: matrix = [[0,1,0],[1,1,1],[0,1,0]], target = 0
Output: 4
Explanation: The four 1x1 submatrices that only contain 0.

Example 2:

Input: matrix = [[1,-1],[-1,1]], target = 0
Output: 5
Explanation: The two 1x2 submatrices, plus the two 2x1 submatrices, plus the 2x2 submatrix.

Example 3:

Input: matrix = [[904]], target = 0
Output: 0 

Constraints:

• 1 <= matrix.length <= 100
• 1 <= matrix[0].length <= 100
• -1000 <= matrix[i] <= 1000
• -10^8 <= target <= 10^8

---

题意

在一个矩阵中找到所有的子矩阵，使得子矩阵的和正好为指定值。

思路

使用前缀和方法解决。首先求出从matrix[0][0]到任意一点组成的子矩阵的和；接着固定子矩阵的上边i和下边j，这个子矩阵的左边是列0，改变右边，计算左侧形成的小矩阵的前缀和，每次计算一个前缀和，要进行两次判断：1. 和本身是否等于目标值；2. 和减去目标值的值是否是之前出现过的前缀和。

---

代码实现

Java

class Solution {
    public int numSubmatrixSumTarget(int[][] matrix, int target) {
        int ans = 0;
        int m = matrix.length, n = matrix[0].length;
        int[][] sum = new int[m][n];

        for (int i = 0; i < m; i++) {
            int tmp = 0;
            for (int j = 0; j < n; j++) {
                tmp += matrix[i][j];
                sum[i][j] = (i == 0 ? 0 : sum[i - 1][j]) + tmp;
            }
        }

        for (int i = 0; i < m; i++) {
            for (int j = i; j < m; j++) {
                Map<Integer, Integer> pre = new HashMap();
                for (int k = 0; k < n; k++) {
                    int cur = sum[j][k] - (i == 0 ? 0 : sum[i - 1][k]);
                    if (cur == target) ans++;
                    if (pre.containsKey(cur - target)) ans += pre.get(cur - target);
                    pre.put(cur, pre.getOrDefault(cur, 0) + 1);
                }
            }
        }

        return ans;
    }
}