【暖*墟】#动态规划# 基环树DP的学习与练习

因为弃置了 四边形不等式优化 ，所以DP的任务还剩下 基环树DP / 插头DP / 动态DP

当然，树形DP / 状压DP / 数位DP / 斜率优化DP 也还是要练习的......

一 . 基环树的定义

基环树：无向图，在一颗树的基础上，添加一条边。环上每个点都是树根。

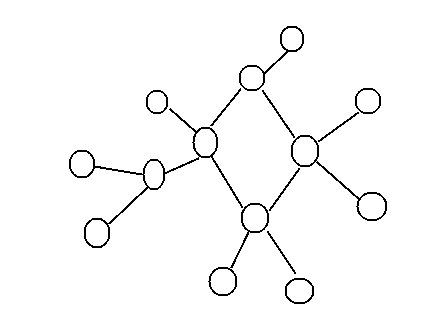
如果进行正常的DP，在环中是无法处理的。所以要把环拆开。

假设要拆开的点是环上连在一起的u、v，这两个点存在限制关系（比如不同时选）。

在拆开后，分别讨论 选择u不选择v，选择v不选择u 两种情况即可。

二 . “找环”操作

在基环树上dfs，找到一个在此结点之前走过的相邻结点、就开始记录环。

vector<int> G[MAXN]; //基环树

int fa[MAXN]; //dfs时的父亲

int dfn[MAXN], idx;  //访问的时间

int loop[MAXN], cnt; //环

void get_loop(int u) {
    dfn[u] = ++ idx; //记录dfn序
    for (int i = 0; i < G[u].size(); i ++) {
        int v = G[u][i]; if(v == fa[u]) continue ;
        if(dfn[v]) { //找到了环
            if(dfn[v] < dfn[u]) continue ;
            loop[++ cnt] = v;
            for ( ; v != u; v = fa[v])
                loop[++ cnt] = fa[v];
        } else fa[v] = u, get_loop(v); //继续递归
    }
}

三 . 有向的基环树

基环内向树：每个点出度为1（因此每个环上点的子树，儿子指向父亲）。

基环外向树：每个点入度为1（因此每个环上点的子树，父亲指向儿子）。

• 将上图的所有边反转一下，就是基环外向树。

四 . 基环树的直径

基环树的直径定义为：基环树中最长的简单路径的长度。

其中，简单路径指不重复经过任何点或边的路径。

那么基环树的直径只可能有两种情况：

1. 不经过环（在环上的某一点的子树中）
2. 经过了环（某一段在环上）

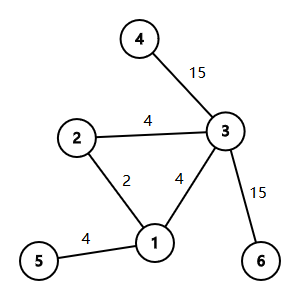此图的直径为15+15（1）

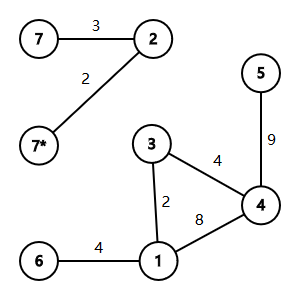此图的直径为4+8+9（2）

（1）【CF835F】 Roads in the Kingdom

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<string>
#include<queue>
#include<vector>
#include<cmath>
#include<map>
using namespace std;
typedef long long ll;

/*【CF835F】 Roads in the Kingdom
求基环树删去环上任意一边后直径最小值。*/

// 因为作者太菜所以请点击：https://www.cnblogs.com/penth/p/9668498.html

void read(int &x){ //读入优化（正负整数）
    int fx=1;x=0;char s=getchar();
    while(s<'0'||s>'9'){if(s=='-')fx=-1;s=getchar();}
    while(s>='0'&&s<='9'){x=(x<<3)+(x<<1)+s-'0';s=getchar();}
    x*=fx; //正负号
}

const int N=201000; const ll inf=0x3f3f3f3f3f3f3f3f;

struct Edge{int ver,nxt,w;}a[N<<1];

int head[N],is[N],st[N],vis[N]; ll f[N],pre[N];

int gl[N],gr[N],hl[N],hr[N],hhl[N],hhr[N],ggl[N],ggr[N];

int n,m,tot,top; ll Ans;

void get_cir(int x,int las){
    if(vis[x]){
        int p=top;
        while(st[p]^x)--p;
        for(int i=p;i<=top;i++)
            is[st[i-p+1]=st[i]]=1;
        st[0]=-1,top-=p-1; return;
    } vis[st[++top]=x]=1;
    for(int i=head[x];i&&~st[0];i=a[i].nxt)
        if(a[i].ver^las) get_cir(a[i].ver,x);
    if(~st[0]) vis[st[top--]]=0;
}

void dfs(int x,int las){
    ll sec=0ll;
    for(int i=head[x];i;i=a[i].nxt)
        if(!is[a[i].ver]&&a[i].ver^las){
            dfs(a[i].ver,x);f[a[i].ver]+=a[i].w;
            if(f[a[i].ver]>=f[x])sec=f[x],f[x]=f[a[i].ver];
            else if(f[a[i].ver]>sec)sec=f[a[i].ver];
    } Ans=max(Ans,f[x]+sec);
}

inline ll G(int x){return x?f[st[x]]-pre[x]:-inf;}
inline ll H(int x){return x?f[st[x]]+pre[x]:-inf;}

void work(){
    st[0]=st[top];
    for(int x=1;x<=top;++x){
        for(int i=head[st[x-1]];i;i=a[i].nxt)
            if(a[i].ver==st[x]){
                pre[x]=pre[x-1]+a[i].w;
                break;
            }
        dfs(st[x],0);
    } for(int i=1;i<=top;i++){
        gl[i]=gl[i-1],ggl[i]=ggl[i-1];
        hl[i]=hl[i-1],hhl[i]=hhl[i-1];
        if(G(i)>G(gl[i])) ggl[i]=gl[i],gl[i]=i;
        else if(G(i)>G(ggl[i])) ggl[i]=i;
        if(H(i)>H(hl[i])) hhl[i]=hl[i],hl[i]=i;
        else if(H(i)>H(hhl[i])) hhl[i]=i;
    } for(int i=top;i;--i){
        gr[i]=gr[i+1],ggr[i]=ggr[i+1];
        hr[i]=hr[i+1],hhr[i]=hhr[i+1];
        if(G(i)>G(gr[i])) ggr[i]=gr[i],gr[i]=i;
        else if(G(i)>G(ggr[i])) ggr[i]=i;
        if(H(i)>H(hr[i])) hhr[i]=hr[i],hr[i]=i;
        else if(H(i)>H(hhr[i])) hhr[i]=i;
    } ll ans; if(hl[top]!=gl[top]) ans=G(gl[top])+H(hl[top]);
    else ans=max(G(ggl[top])+H(hl[top]),G(gl[top])+H(hhl[top]));
    for(int i=1;i<top;i++){
        ll val=pre[top]+H(hl[i])+G(gr[i+1]),tmp;
        if(gl[i]^hl[i]) tmp=G(gl[i])+H(hl[i]);
        else tmp=max(G(ggl[i])+H(hl[i]),G(gl[i])+H(hhl[i]));
        val=max(val,tmp); i++;
        if(gr[i]^hr[i]) tmp=G(gr[i])+H(hr[i]);
        else tmp=max(G(ggr[i])+H(hr[i]),G(gr[i])+H(hhr[i]));
        val=max(val,tmp); i--; ans=min(ans,val);
    } cout<<max(ans,Ans)<<endl;
}

void init(){
    read(n); for(int i=1,u,v,w;i<=n;i++){
        read(u),read(v),read(w);
        a[++tot].ver=v,a[tot].w=w,a[tot].nxt=head[u],head[u]=tot;
        a[++tot].ver=u,a[tot].w=w,a[tot].nxt=head[v],head[v]=tot;
    } get_cir(1,1);
}

int main(){init();work();return 0;}

（2）【p4381】Island

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<string>
#include<queue>
#include<vector>
#include<cmath>
#include<map>
using namespace std;
typedef long long ll;

/*【p4381】Island
有一个基环树和树组成的森林，共有n个结点。
边有边权。试求其中所有联通块的直径之和。 */

const int Maxn=1e6+7;

int n,dfn[Maxn],id,headd[Maxn],tot,cnt;

int vis[Maxn],que[2*Maxn],pd[Maxn],fa[Maxn],dvi[Maxn];

long long las,nic,dep[2*Maxn],Q[2*Maxn],dis[Maxn],ans;

struct Edge{ int ver,nextt,w; }e[4*Maxn];

struct Hoop{ int ver,w; }edge[Maxn],ring[Maxn];

int read(){ int s=0,w=1; char ch=getchar();
  while(ch<'0'||ch>'9'){if(ch=='-') w=-1;ch=getchar();}
  while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar(); return s*w; }

inline void add(int x,int y,int w)
 { e[++tot].ver=y,e[tot].nextt=headd[x],e[tot].w=w,headd[x]=tot; }

inline long long K(int x){ return dep[x]-Q[x]; }

inline void find_hoop(int x){ //找树上的环
    dvi[x]=1; while(1){ int y=edge[x].ver; //只有一条连边
        if(dvi[y]){ ring[++cnt].ver=y,ring[cnt].w=edge[y].w,dfn[y]=1;
            for(int i=x;i!=y;i=fa[i]) 
                dfn[i]=1,ring[++cnt].ver=i,ring[cnt].w=edge[i].w; break;
        } dvi[y]=1,fa[y]=x,x=y; //继续往下寻找
    }
}

inline void dp(int x){ //树形dp
    vis[x]=1; dfn[x]=1;
    for(int i=headd[x];i;i=e[i].nextt){
        int y=e[i].ver;
        if(vis[y]||pd[y]) continue; dp(y);
        nic=max(nic,dis[x]+dis[y]+e[i].w);
        dis[x]=max(dis[x],dis[y]+e[i].w); 
    }
}

void dfs(int x,int fa,long long w){ //求环上每个节点的dep值
    if(w>=nic) nic=w;
    for(int i=headd[x];i;i=e[i].nextt){
        int u=e[i].ver;
        if(u!=fa&&!pd[u]) dfs(u,x,w+e[i].w);
    }
}

inline void first(int i){
    nic=0;dfs(ring[i].ver,0,0);dep[i]=nic; 
    nic=0;dp(ring[i].ver);las=max(las,nic);
}

inline void quee(){ //单调队列优化
    int head=1,tail=0;
    for(int i=1;i<=2*cnt;i++){
        if(i<=cnt) Q[i]=Q[i-1]+ring[i].w;
        else Q[i]=Q[i-1]+ring[i-cnt].w;
        if(head<=tail) las=max(las,K(que[head])+Q[i]+dep[i]);
        while(head<=tail&&K(que[tail])<=K(i)) --tail;
        que[++tail]=i;
        while(head<=tail&&que[head]<=i-cnt+1) ++head;
    } ans+=las;
}

int main(){
    n=read(); for(int i=1,y,w;i<=n;i++){
        y=read(),w=read(),add(i,y,w),add(y,i,w);
        edge[i].ver=y,edge[i].w=w;
    } for(int i=1;i<=n;i++){ if(dfn[i]) continue;
        cnt=0,id=0,las=0,find_hoop(i);
        for(int j=1;j<=cnt;j++) pd[ring[j].ver]=1;
        for(int j=1;j<=cnt;j++) first(j);
        for(int j=1;j<=cnt;j++) dep[j+cnt]=dep[j]; 
        quee();
    } printf("%lld
",ans); return 0;
}

五 . 相关例题详解

（1）【P2607】[ZJOI2008] 骑士

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<string>
#include<queue>
#include<vector>
#include<cmath>
#include<map>
using namespace std;
typedef long long ll;

#define N 1000010

int fun[N],a,b; long long f[N][2];

struct node{ int next,to,v; }e[2*N];

int st[N],vis[N],n,s,tot,x1,x2,E;

void add(int x,int y){e[tot].to=y,e[tot].next=st[x],st[x]=tot++;}

void find_circle(int x,int pre){
    vis[x]=1; for (int i=st[x];~i;i=e[i].next){
        if ((i^1)==pre) continue;
        if (vis[e[i].to]){ x1=x,x2=e[i].to; E=i; continue; }
        find_circle(e[i].to,i);
    }
}

void dfs(int x,int pre){
    f[x][0]=0; f[x][1]=fun[x];
    for (int i=st[x];~i;i=e[i].next){
        if ((i^1)==pre) continue;
        if (i==E || (i^1)==E) continue;
        dfs(e[i].to,i);
        f[x][1]+=f[e[i].to][0];
        f[x][0]+=max(f[e[i].to][1],f[e[i].to][0]);
    }
}

int main(){
    memset(st,-1,sizeof st);
    scanf("%d",&n);
    for (int i=1;i<=n;i++)
        scanf("%d%d",&a,&b),add(i,b),add(b,i),fun[i]=a;
    long long ans=0;
    for (int i=1;i<=n;i++) {
        if (vis[i]) continue;
        find_circle(i,-2); dfs(x1,-1);
        long long temp=f[x1][0]; dfs(x2,-1);
        temp=max(temp,f[x2][0]); ans+=temp; 
    } printf("%lld
",ans);
}

（2）【p3533】rendezous

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<string>
#include<queue>
#include<vector>
#include<cmath>
#include<map>
using namespace std;
typedef long long ll;

/*【p3533】rendezous
给定一棵内向森林，多次给定两个点a和b，求点对(x,y)满足：
1.从a出发走x步和从b出发走y步会到达同一个点
2.在1的基础上如果有多解，那么要求max(x,y)最小
3.在1和2的基础上如果有多解，那么要求min(x,y)最小
4.如果在1、2、3的基础上仍有多解，那么要求x>=y。 */

//n个点n条边且每个点都有出边，是环套树森林。dfs把环套树拆成一堆树，用倍增求LCA。

void reads(int &x){
    int fx=1;x=0;char s=getchar();
    while(s<'0'||s>'9'){if(s=='-')fx=-1;s=getchar();}
    while(s>='0'&&s<='9'){x=(x<<3)+(x<<1)+(s-'0');s=getchar();}
    x=x*fx; //正负号
}

const int N=500019;

int n,fa[N][20],root,q,circle[N],dep[N];
int num[N],sum[N],tot,pos[N],vis[N];

void findcircle(int x){
    int now=x;
    for(;;x=fa[x][0]){ //不停地找fa
        if(vis[x]==now) break;
        if(vis[x]) return;
        vis[x]=now;
    } tot++;
    while(!circle[x]){
        circle[x]=x; dep[x]=1;
        num[x]=++sum[tot];
        pos[x]=tot; x=fa[x][0];
    }
}

void dfs(int x){
    if(dep[x]) return;
    dfs(fa[x][0]);
    circle[x]=circle[fa[x][0]];
    dep[x]=dep[fa[x][0]]+1;
    for(int i=1;(1<<i)<dep[x];i++)
    fa[x][i]=fa[fa[x][i-1]][i-1];
}

inline int lca(int x,int y){
    if(dep[x]<dep[y]) swap(x,y);
    int t=dep[x]-dep[y];
    for(int i=18;~i;i--)
        if(t&(1<<i)) x=fa[x][i];
    if(x==y) return x;
    for(int i=18;~i;i--)
        if(fa[x][i]!=fa[y][i]) x=fa[x][i],y=fa[y][i];
    return fa[x][0];
}

bool judge(int a,int b,int c,int d){
    if(max(a,b)<max(c,d)) return 1;
    if(max(a,b)>max(c,d)) return 0;
    if(min(a,b)<min(c,d)) return 1;
    if(min(a,b)>min(c,d)) return 0;
    if(a>=b) return 1; return 0;
}

int main(){
    reads(n),reads(q);
    for(int i=1;i<=n;i++) reads(fa[i][0]);
    for(int i=1;i<=n;i++) findcircle(i);
    for(int i=1;i<=n;i++)
        if(!circle[i]) dfs(i);
    while(q--){
        int x,y; reads(x),reads(y);
        if(pos[circle[x]]!=pos[circle[y]]){
            puts("-1 -1"); continue; //不是同一个环
        } if(circle[x]==circle[y]){
            printf("%d %d
",dep[x]-dep[lca(x,y)],dep[y]-dep[lca(x,y)]); continue;
        } int ans1=dep[x]-1,ans2=dep[y]-1,t=pos[circle[x]];
        x=num[circle[x]],y=num[circle[y]];
        int z1=(sum[t]+y-x)%sum[t],z2=sum[t]-z1;
        if(judge(ans1+z1,ans2,ans1,ans2+z2))
        printf("%d %d
",ans1+z1,ans2);
        else printf("%d %d
",ans1,ans2+z2);
    }
}

 参考学习：https://blog.csdn.net/zzrh2018/article/details/81878766

                  https://www.cnblogs.com/mangoyang/p/9314823.html

                            ——时间划过风的轨迹，那个少年，还在等你