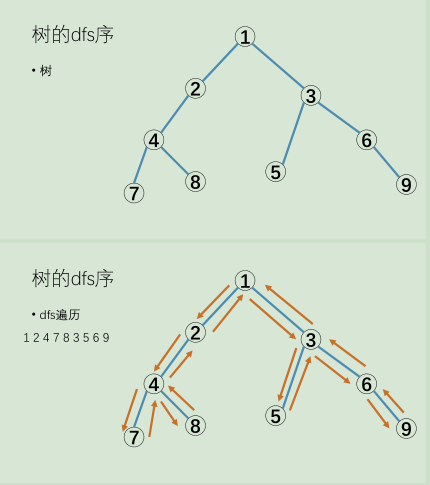
虚树,就是不真实的树。往往出现在一类树形动态规划问题中。
换句话说,虚树就是为了解决一类树形动态规划问题而诞生的。
【例题1】[SDOI2011]消耗战
- 给出一棵树,每条边有边权。有m次询问,每次询问给出k个点。
- 问使得这k个点均不与1号点(根节点)相连的最小代价。
- 数据范围:n<=250000, m>=1, ∑k<=500000。
[暴力dp] 首先考虑m=1,也就是只有一次询问的情况。
我们考虑暴力dp:设f[x]为处理完以x为根的树的最小代价。
转移分为两种情况:1.断开自己与根的联系,代价为从根到该节点的最小值;
2.若该节点不是询问点、不考虑断开,求断开子树内的所有询问点的最小代价;
但是这样的复杂度是O(nm)的,显然无法AC。
然而我们发现∑k是比较小的,可不可以对k下手呢?于是,虚树诞生了。
虚树的主要思想:对于一棵树,仅仅保留有用的点,重新构建一棵树。
- 这里有用的点指的是询问点和它们的lca。
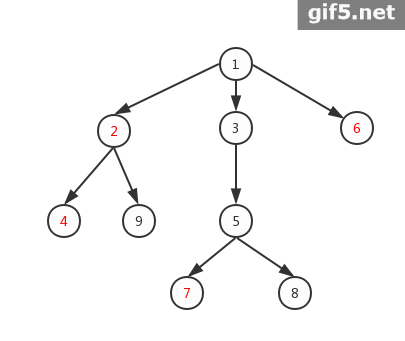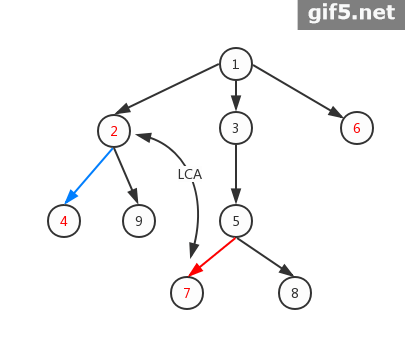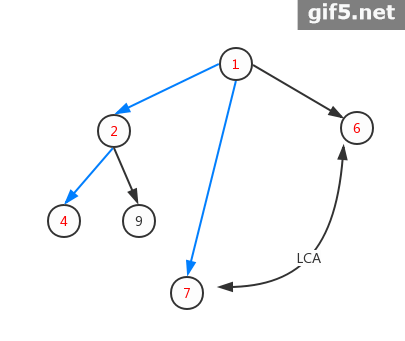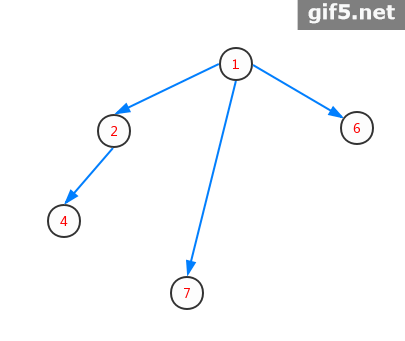
比如这样的一棵树:

对于样例中的三次询问:
3
2 10 6
4 5 7 8 3
3 9 4 6
那么它的虚树分别长这样:
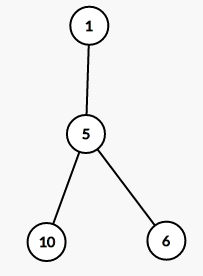
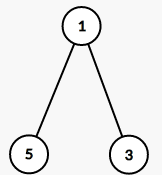
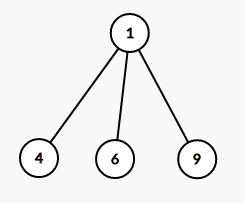
- 注意:图二中,断了5就一定会断了7、8,所以不用考虑7、8。
得到了询问点,考虑如何构造出一棵虚树。
首先要先对整棵树dfs一遍,求出dfs序,每个节点以dfs序为关键字从小到大排序。
同时 维护一个栈,表示 从根到栈顶元素这条链 。
假设当前要加入的节点为p,栈顶元素为x=s[top],lca为他们的最近公共祖先。
因为我们是按照dfs序遍历,因此lca不可能是p。
那么现在会有两种情况: 1. lca是x,直接将p入栈。
2. x,p分别位于lca的两棵子树中,那么此时x这棵子树已经遍历完毕。
上述2中,如果没有遍历完毕,则x的子树中还有一个未加入的点y,
但是dfn[y]<dfn[p],即:应先访问y。所以没有遍历完毕。
当x这棵子树已经遍历完毕时,我们需要对其进行构建。
设栈顶元素为x,栈顶第二个元素为y(到达x的某一条链)。
若dfn[y]>dfn[lca],可以连边y—>x,将x出栈;
若dfn[y]=dfn[lca],即y=lca,连边lca−>x,子树构建完毕;
若dfn[y]<dfn[lca],即lca在y,x之间,连边lca−>x,x出栈,lca入栈,子树构建完毕。
不断重复这个过程,虚树就构建完成了。另外需要维护链上最小值,然后直接在虚树上dp。

void insert(int x){ //建立虚树
if(top==1){ sta[++top]=x; return; }
int lca=LCA(x,sta[top]); if(lca==sta[top]) return;
//1.若dfn[y]>dfn[lca],可以连边y—>x,将x出栈;
while(top>1&&dfn[sta[top-1]]>=dfn[lca]) add_edge(sta[top-1],sta[top]),top--;
if(lca!=sta[top]) add_edge(lca,sta[top]),sta[top]=lca; sta[++top]=x;
}
- 借某大佬的图解:
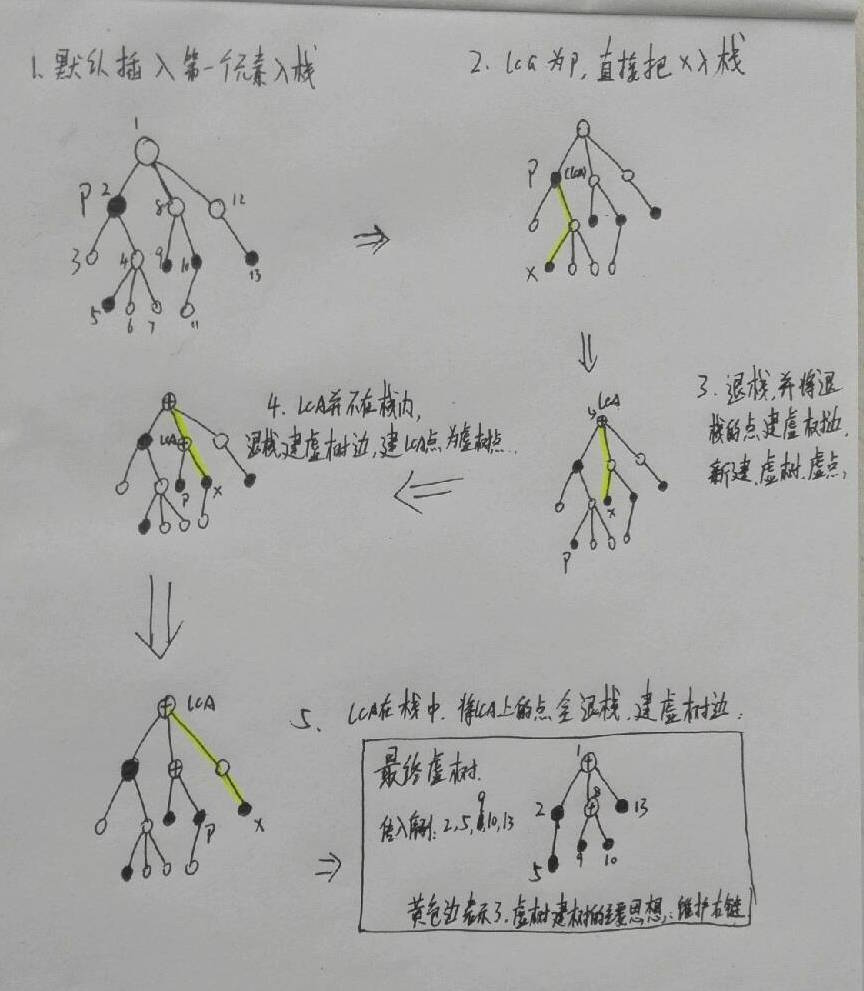
【p2495】消耗战 代码实现:
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<string>
#include<queue>
#include<vector>
#include<cmath>
#include<map>
using namespace std;
typedef long long ll;
//【p2495】消耗战 // 树形dp + 虚树
void reads(int &x){ //读入优化(正负整数)
int fx=1;x=0;char s=getchar();
while(s<'0'||s>'9'){if(s=='-')fx=-1;s=getchar();}
while(s>='0'&&s<='9'){x=(x<<3)+(x<<1)+s-'0';s=getchar();}
x*=fx; //正负号
}
const int N=250019; int n,m;
struct Edge{ int u,v,w,nextt; }e[N*2];
int head[N],tot=0;
inline void add(int x,int y,int z)
{ e[++tot]=(Edge){x,y,z,head[x]}; head[x]=tot; }
vector<int> v[N]; void add_edge(int x,int y){ v[x].push_back(y); }
int top_[N],siz[N],son[N],dep[N],fa[N];
int dfn[N],ID=0,a[N],sta[N],top; ll minn[N];
//-------------树链剖分部分-----------------//
void dfs1(int u,int _fa){
siz[u]=1,fa[u]=_fa;
for(int i=head[u];i!=-1;i=e[i].nextt){
if(e[i].v==_fa) continue; dep[e[i].v]=dep[u]+1;
minn[e[i].v]=min(minn[u],(ll)e[i].w); //到根节点的链上的最小边
dfs1(e[i].v,u),siz[u]+=siz[e[i].v];
if(siz[e[i].v]>siz[son[u]]) son[u]=e[i].v; }
}
void dfs2(int x,int top_fa){
top_[x]=top_fa,dfn[x]=++ID; if(!son[x]) return;
dfs2(son[x],top_fa); //先走重儿子
for(int i=head[x];i!=-1;i=e[i].nextt)
if(!top_[e[i].v]) dfs2(e[i].v,e[i].v);
}
int LCA(int x,int y){
while(top_[x]!=top_[y]){
if(dep[top_[x]]<dep[top_[y]]) swap(x,y);
x=fa[top_[x]];
} if(dep[x]<dep[y]) swap(x,y); return y;
}
//------------虚树树形DP部分---------------//
void insert(int x){ //建立虚树
if(top==1){ sta[++top]=x; return; }
int lca=LCA(x,sta[top]); if(lca==sta[top]) return;
//1.若dfn[y]>dfn[lca],可以连边y—>x,将x出栈;
while(top>1&&dfn[sta[top-1]]>=dfn[lca]) add_edge(sta[top-1],sta[top]),top--;
if(lca!=sta[top]) add_edge(lca,sta[top]),sta[top]=lca; sta[++top]=x;
}
ll dp(int x){ //在虚树上直接dp
if(v[x].size()==0) return minn[x];
ll sum=0; for(int i=0;i<v[x].size();i++) sum+=dp(v[x][i]);
v[x].clear(); return min(sum,(ll)minn[x]);
}
//-------------主程序部分-----------------//
bool cmp(const int &a,const int &b){ return dfn[a]<dfn[b]; }
int main(){
memset(head,-1,sizeof(head)); minn[1]=1ll<<60; reads(n);
for(int i=1,x,y,z;i<n;i++)
reads(x),reads(y),reads(z),add(x,y,z),add(y,x,z);
dep[1]=1,dfs1(1,0),dfs2(1,1); reads(m);
while(m--){ int k; reads(k);
for(int i=1;i<=k;i++) reads(a[i]);
sort(a+1,a+k+1,cmp); //将这些节点以dfn序排序
sta[top=1]=1; for(int i=1;i<=k;i++) insert(a[i]);
while(top>0) add_edge(sta[top-1],sta[top]),top--; //虚树连边
cout<<dp(1)<<endl; //在虚树上直接树形dp
}
}
——时间划过风的轨迹,那个少年,还在等你。