斯坦纳树的简介
斯坦纳树就是在给定边集中找最短网络(给定点+扩展点)使给定点联通。
包含给定K个节点的最小生成树,一般K很小,在网格图上。
f[i][s]表示以点i为根,已和s集合里的点联通的生成树的最小代价。
【例题】[WC2008] 游览计划
.jpg)

DP の 两种转移方案
1. i的不同子树的合并,f[i][s]=min{ f[i][s']+f[i][s-s']-cost[i] };
2. 考虑添加给定子集外的点的情况,f[i][s]=f[j][s]+a[i][j];
即:从一棵合法的树一个点一个点向外扩张;
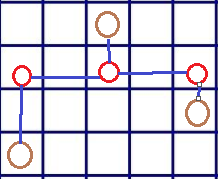
比如这棵树,褐色是给定点集,下面两个褐色点联通后从中间的红点向上扩张,
在最上面的褐点的位置再用第一种转移合并即可得到以最上面的褐点为根的这棵树。
具体解题思路
所求路径是一颗斯坦纳树。点数K ≤ 10,所以可以用2进制状压来表示点的连接状态。
定义 f[x][y][o] 表示以(x, y)为根的树满足二进制状态o时需要的最小代价。
<1> f[x][y][o] = f[x][y][o1] + f[x][y][o2] - a[x][y] (o = o1 | o2)
<2> f[x][y][o] = f[p][q][o] + a[x][y] (点(x, y)与 点(p, q)相邻)
- 对于式<1>, 用普通的DP维护即可。
- 对于式<2>, 对于相邻两点,不能直接确定更新关系。
对于式<2>,可以想到最短路中的dist[]数组更新,即:SPFA维护 dist[u1] <= dist[u2] + w[u1][u2] 。
在维护了<1>后,f[x][y][o]不为INF的点,可以先入SPFA的队列,以便更新其他点。
1. 依次枚举状态o; 2. 对于某一状态, 枚举点(x, y),用 <1> 维护更新;
3. f[x][y][o]不为INF的点入队; 4. SPFA 维护 <2> ; 5. 维护更新状态为o的情况。
答案输出问题只需要在转移时记下前驱, 在输出前递归标记最优路径即可。
相关例题分析
【例题1】【p4294】游览计划
#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #include<string> #include<queue> #include<vector> #include<cmath> #include<map> using namespace std; typedef long long ll; //【p4294】游览计划 // [斯坦纳树] // f[x][y][o] 即以(x, y)为根的树满足二进制状态o时需要的最小代价。 // <1> f[x][y][o] = f[x][y][o1] + f[x][y][o2] - a[x][y] (o = o1 | o2) // <2> f[x][y][o] = f[p][q][o] + a[x][y] (点(x, y)与 点(p, q)相邻) void reads(int &x){ //读入优化(正负整数) int fx=1;x=0;char s=getchar(); while(s<'0'||s>'9'){if(s=='-')fx=-1;s=getchar();} while(s>='0'&&s<='9'){x=(x<<3)+(x<<1)+s-'0';s=getchar();} x*=fx; //正负号 } int n,m,tot=0,a[12][12],vis[12][12],f[12][12][5019]; const int dx[5]={-1,1,0,0}; const int dy[5]={0,0,-1,1}; struct PRE{ int x,y,S; }Pre[12][12][5019]; queue< pair<int,int> >q; //SPFA队列 void SPFA(int sta){ while(q.size()!=0){ pair<int,int> p=q.front(); q.pop(); vis[p.first][p.second]=0; for(int i=0;i<4;i++){ int wx=p.first+dx[i],wy=p.second+dy[i]; if(wx<1||wx>n||wy<1||wy>m) continue; if(f[wx][wy][sta]>f[p.first][p.second][sta]+a[wx][wy]){ f[wx][wy][sta]=f[p.first][p.second][sta]+a[wx][wy]; Pre[wx][wy][sta]=(PRE){p.first,p.second,sta}; if(!vis[wx][wy]) vis[wx][wy]=1,q.push(make_pair(wx,wy)); } } } } void dfs(int x,int y,int now){ vis[x][y]=1; PRE tmp=Pre[x][y][now]; if(tmp.x==0&&tmp.y==0) return; dfs(tmp.x,tmp.y,tmp.S); //回到上一步 if(tmp.x==x&&tmp.y==y) dfs(tmp.x,tmp.y,now-tmp.S); } int main(){ reads(n),reads(m); memset(f,0x3f,sizeof(f)); for(int i=1;i<=n;i++) for(int j=1;j<=m;j++){ reads(a[i][j]); if(a[i][j]==0) f[i][j][1<<tot]=0,tot++; } //记录景点 for(int sta=0;sta<=(1<<tot)-1;sta++){ //枚举当前状态sta for(int i=1;i<=n;i++) for(int j=1;j<=m;j++){ for(int s=sta;s;s=(s-1)&sta){ //枚举先前的状态s if(f[i][j][s]+f[i][j][sta-s]-a[i][j]<f[i][j][sta]) f[i][j][sta]=f[i][j][s]+f[i][j][sta-s]-a[i][j], Pre[i][j][sta]=(PRE){i,j,s}; //情况1:(i,j)不同子树的合并 } if(f[i][j][sta]<1e9) q.push(make_pair(i,j)),vis[i][j]=1; } SPFA(sta); //用SPFA更新情况2:相邻节点到达情况+选择此地的代价 } int ansx,ansy,flag=0; for(int i=1;i<=n&&!flag;i++) for(int j=1;j<=m;j++) if(!a[i][j]){ ansx=i,ansy=j; flag=1; break; } //随意找一个起点 printf("%d ",f[ansx][ansy][(1<<tot)-1]); //各处景点相连的代价一定相同 memset(vis,0,sizeof(vis)); dfs(ansx,ansy,(1<<tot)-1); for(int i=1;i<=n;i++,puts("")){ //输出答案:具体方案 for(int j=1;j<=m;j++){ if(a[i][j]==0) putchar('x'); else if(vis[i][j]) putchar('o'); else putchar('_'); } } }
【例题2】【p3264】管道连接
#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #include<string> #include<queue> #include<vector> #include<cmath> #include<map> using namespace std; typedef long long ll; //【p3264】管道连接 // [斯坦纳树] // f[x][o] 即以x为根的子树满足二进制状态o时需要的最小代价。 // <1> f[x][o] = f[x][o1] + f[x][o-o1] ; // <2> f[x][o] = f[p][o] + w[x][p] (点x与点p相邻) ; // g[o]表示,颜色联通性为sta时的最小值,枚举子集转移即可。 void reads(int &x){ //读入优化(正负整数) int fx=1;x=0;char s=getchar(); while(s<'0'||s>'9'){if(s=='-')fx=-1;s=getchar();} while(s>='0'&&s<='9'){x=(x<<3)+(x<<1)+s-'0';s=getchar();} x*=fx; //正负号 } const int N=1000019; struct node{ int nextt,ver,w; }e[N*2]; int n,m,p,tot=1,head[N],vis[N],sum[N]; void add(ll x,ll y,ll z) { e[++tot].ver=y,e[tot].nextt=head[x],e[tot].w=z,head[x]=tot; } struct Point{ int col,id; }a[N]; int f[2019][2019],g[2019]; queue< int >q; //SPFA队列 void SPFA(int sta){ while(q.size()!=0){ int x=q.front(); q.pop(); vis[x]=0; for(int i=head[x];i;i=e[i].nextt){ if(f[e[i].ver][sta]>f[x][sta]+e[i].w){ f[e[i].ver][sta]=f[x][sta]+e[i].w; if(!vis[e[i].ver]) vis[e[i].ver]=1,q.push(e[i].ver); } } } } bool check(int sta){ int tmp[11]; memset(tmp,0,sizeof(tmp)); for(int i=1;i<=10;i++) if(sta&(1<<i-1)) tmp[a[i].col]++; for(int i=1;i<=10;i++) //有相同频道的未相连 if(tmp[i] && tmp[i]!=sum[i]) return false; return true; //任意相同频道的情报站之间都建立通道连接 } int main(){ reads(n),reads(m),reads(p); memset(f,0x3f,sizeof(f)); for(int i=1,x,y,z;i<=m;i++) reads(x),reads(y),reads(z),add(x,y,z),add(y,x,z); memset(f,0x3f,sizeof(f)),memset(g,0x3f,sizeof(g)); for(int i=1;i<=p;i++) reads(a[i].col),reads(a[i].id), sum[a[i].col]++,f[a[i].id][1<<(i-1)]=0; //输入重要情报站 for(int sta=0;sta<=(1<<p)-1;sta++){ //枚举当前状态sta for(int i=1;i<=n;i++){ //↓↓枚举前一步的状态s for(int s=sta;s;s=(s-1)&sta) //情况1:(i,j)不同子树的合并 f[i][sta]=min(f[i][sta],f[i][s]+f[i][sta-s]); if(f[i][sta]<0x3f3f3f3f) q.push(i),vis[i]=1; } SPFA(sta); //用SPFA更新情况2:相邻节点到达情况+选择此地的代价 } for(int sta=0;sta<=(1<<p)-1;sta++) for(int i=1;i<=n;i++) g[sta]=min(g[sta],f[i][sta]); for(int sta=0;sta<=(1<<p)-1;sta++) if(check(sta)) for(int s=sta;s;s=(s-1)&sta) if(check(s)) //s可行,sta可行 g[sta]=min(g[sta],g[s]+g[sta-s]); //那么sta-s也一定可行 printf("%d ",g[(1<<p)-1]); return 0; }
——时间划过风的轨迹,那个少年,还在等你