797. All Paths From Source to Target

问题：

给定一个【0～n-1】n个节点构成的有向图，

求从0到n-1的所有路径。

graph[i]=[a,b,c...]

指：节点i 指向 节点a,b,c...

Example 1:
Input: graph = [[1,2],[3],[3],[]]
Output: [[0,1,3],[0,2,3]]
Explanation: There are two paths: 0 -> 1 -> 3 and 0 -> 2 -> 3.

Example 2:
Input: graph = [[4,3,1],[3,2,4],[3],[4],[]]
Output: [[0,4],[0,3,4],[0,1,3,4],[0,1,2,3,4],[0,1,4]]

Example 3:
Input: graph = [[1],[]]
Output: [[0,1]]

Example 4:
Input: graph = [[1,2,3],[2],[3],[]]
Output: [[0,1,2,3],[0,2,3],[0,3]]

Example 5:
Input: graph = [[1,3],[2],[3],[]]
Output: [[0,1,2,3],[0,3]] 

Constraints:
n == graph.length
2 <= n <= 15
0 <= graph[i][j] < n
graph[i][j] != i (i.e., there will be no self-loops).
The input graph is guaranteed to be a DAG.

 Example 1：

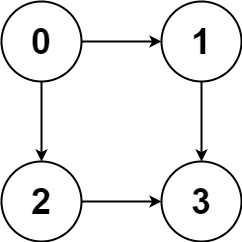
 Example 2:

解法：Backtracking（回溯算法）

• 状态：到当前节点为止，加入的路径path。
• 选择：当前节点 i 的下一个节点 graph[i] list
  • 当前节点：path的最后一位。
• 退出递归条件：path的最后一位=n-1

代码参考：

class Solution {
public:
    void dfs(vector<vector<int>>& res, vector<int>& path, vector<vector<int>>& graph, int pos) {
        if(path[pos]==graph.size()-1) {
            res.push_back(path);
            return;
        }
        if(pos==graph.size()) {
            return;
        }
        for(int nxt:graph[path[pos]]) {
            path.push_back(nxt);
            dfs(res, path, graph, pos+1);
            path.pop_back();
        }
        return;
    }
    vector<vector<int>> allPathsSourceTarget(vector<vector<int>>& graph) {
        vector<vector<int>> res;
        vector<int> path(1,0);
        dfs(res, path, graph, 0);
        return res;
    }
};