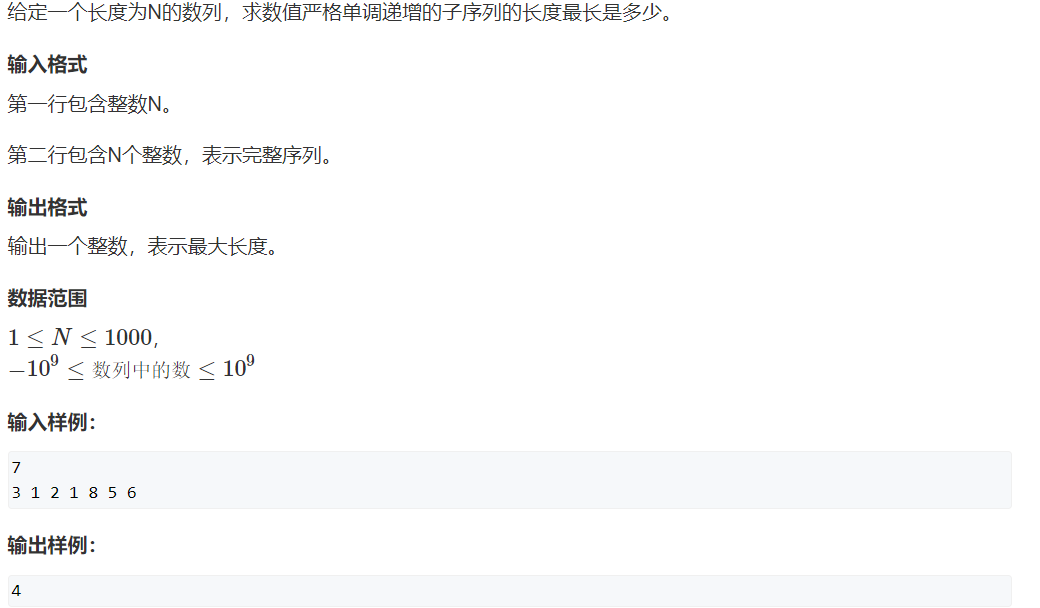

如果不存在就不用去求最大值了,我们只求存在的最大值
如果存在,比如上一个数是j,且a[j] < a[i]
aj ai这种情况
dp[j] + 1
所以dp[i] = max(dp[j] + 1),需满足aj < ai,j = 0, 1, ..., i - 1
时间复杂度:n * n
1 #include <bits/stdc++.h> 2 using namespace std; 3 const int N = 1010; 4 int a[N], dp[N]; 5 int main() { 6 int n; 7 cin >> n; 8 for (int i = 1; i <= n; i++) { 9 cin >> a[i]; 10 } 11 for (int i = 1; i <= n; i++) { 12 dp[i] = 1; //以i结尾的上升子序列长度为1的情况,就是只有a[i]一个数 13 for (int j = 1; j < i; j++) { //枚举左边那个是哪个数 14 if (a[j] < a[i]) { 15 dp[i] = max(dp[i], dp[j] + 1); 16 } 17 } 18 } 19 int res = 0; 20 for (int i = 1; i <= n; i++) { 21 res = max(res, dp[i]); 22 } 23 cout << res << endl; 24 return 0; 25 }
然后怎样把最长上升序列保存下来呢
我们用g数组存储一下每一个转移是怎么转移过来的
第五 二 51
1 #include <bits/stdc++.h> 2 using namespace std; 3 const int N = 1010; 4 int a[N], dp[N], g[N]; 5 int main() { 6 int n; 7 cin >> n; 8 for (int i = 1; i <= n; i++) { 9 cin >> a[i]; 10 } 11 for (int i = 1; i <= n; i++) { 12 dp[i] = 1; 13 g[i] = 0; //表示只有一个数 14 for (int j = 1; j < i; j++) { 15 if (a[j] < a[i]) { 16 //dp[i] = max(dp[i], dp[j] + 1); 17 if (dp[i] < dp[j] + 1) { 18 dp[i] = dp[j] + 1; 19 g[i] = j; 20 } 21 } 22 } 23 } 24 int k = 1; //记最优解的下标 25 for (int i = 1; i <= n; i++) { 26 if (dp[k] < dp[i]) { 27 k = i; 28 } 29 } 30 cout << dp[k] << endl; 31 for (int i = 0, len = dp[k]; i < len; i++) { 32 cout << a[k] << " "; 33 k = g[k]; 34 } 35 return 0; 36 }