◇例题·II◇ Berland and the Shortest Paths
题目来源:Codeforce 1005F +传送门+
◆ 简单题意
给定一个n个点、m条边的无向图。保证图是连通的,且m≥n-1。
以首都(1节点)为根节点生成最小树。树的值定义为每个节点的深度和(根节点深度0)。举个例子:
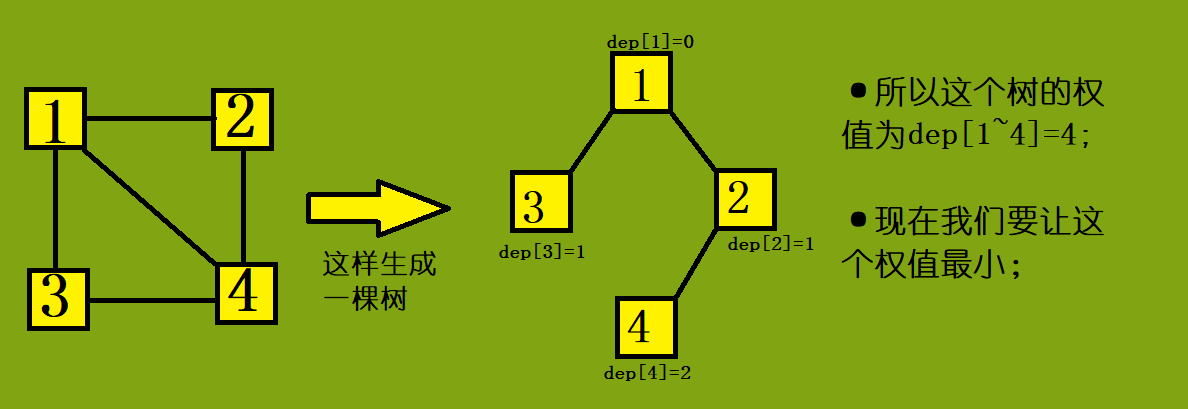
而我们知道,可能有多种情况使树的权值最小,题目给出了一个整数k,如果最小树的生成方案数为ans,当 ans≤k 时,将 ans 种方案全部输出;当 ans>k 时,任意输出 k 种不同生成方案即可。输出方案格式为一个01串,第i个字符如果为0,表示不选第i条边(按照输入顺序),1为选择第i条边。
◆ 解析
其实点 i 的深度 dep[i] 就是根节点1到 i 的路径,而我们知道 1 到 i 没有任何一条路径短于它们的最短路径,所以生成树的权值最小时,根节点到每个点的距离就是原图中根节点到每个节点的最短路径。也就是说,我们生成的最小树就是一个最短路径树。然而显然有时候存在多条最短路径,这也就造成了我们生成的最小树有多种解。于是我们假装生成一棵树,实际上只是生成一个图。
由于这道题的边权都是等价的(不如就把边权看成1吧),我们可以用BFS直接求得最短路,所以说其实这也是一个BFS序图。为了考虑每种情况,我们把所有最小的BFS序边连上。下面再举一个生成BFS序图的例子(希望入门reader可以理解):
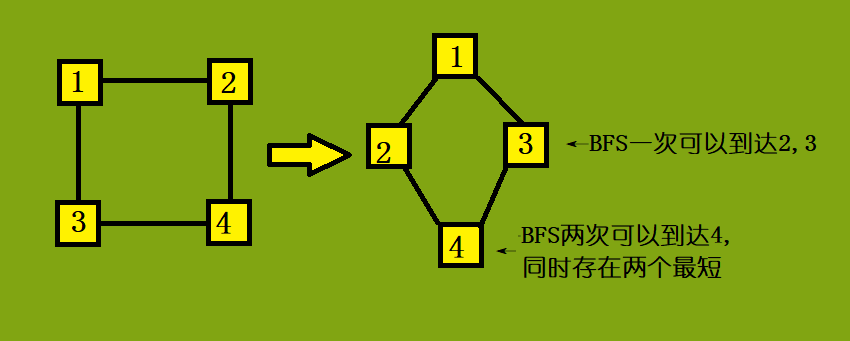
这样我们就生成了一个BFS序有根图,由于我们要生成树,而树的每一个节点的父节点少于一个。在上图中,4的父节点有两个,因此需要断开一条边——两条边是等价的,断掉任意一条即可。
我们可以把 u→v 的边存入v的边集 min_edg[v] ,那么最小权值树则是对于每一个除根节点之外的 v,选择 min_edg[v] 中的任意一条边,所以方案总数为 (除去根节点 i:2~n)min_edg[v]的边数之积。最后再DFS递归求方案即可(具体见代码)。
◆ 源代码
1 /*Lucky_Glass*/ 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<vector> 6 #include<queue> 7 using namespace std; 8 const int MAXN=int(2e5); 9 const int INF=int(1e9); 10 int n_pnt,n_edg,k; 11 int dis[MAXN+5]; 12 vector<pair<int,int> > lnk[MAXN+5]; 13 vector<pair<int,int> > min_edg[MAXN+5]; 14 void BFS(int start) 15 { 16 fill(dis,dis+MAXN+5,INF); 17 dis[start]=0; 18 queue<int> que; 19 que.push(start); 20 while(!que.empty()) 21 { 22 int u=que.front();que.pop(); 23 for(int i=0;i<lnk[u].size();i++) 24 { 25 int v=lnk[u][i].first,id=lnk[u][i].second,Stp=dis[u]+1; 26 if(Stp>dis[v]) continue; 27 min_edg[v].push_back(make_pair(u,id)); 28 if(Stp!=dis[v]) 29 dis[v]=Stp,que.push(v); 30 } 31 } 32 } 33 bool chose[MAXN+5];int cnt; 34 void DFS(int v) 35 { 36 if(v==n_pnt+1) 37 { 38 cnt++; 39 for(int i=1;i<=n_edg;i++) 40 printf("%d",chose[i]); 41 printf(" "); 42 return; 43 } 44 for(int i=0;i<min_edg[v].size();i++) 45 { 46 chose[min_edg[v][i].second]=true; 47 DFS(v+1); 48 chose[min_edg[v][i].second]=false; 49 if(cnt==k) return; 50 } 51 } 52 int main() 53 { 54 scanf("%d%d%d",&n_pnt,&n_edg,&k); 55 for(int i=0,u,v;i<n_edg;i++) 56 scanf("%d%d",&u,&v), 57 lnk[u].push_back(make_pair(v,i+1)), 58 lnk[v].push_back(make_pair(u,i+1)); 59 BFS(1); 60 long long ans=1; 61 for(int i=2;i<=n_pnt;i++) 62 { 63 ans*=min_edg[i].size(); 64 if(ans>k) break; 65 } 66 printf("%lld ",min(k*1ll,ans)); 67 DFS(2); 68 return 0; 69 }
The End
Thanks for reading!
- Lucky_Glass
(Tab:如果我有没讲清楚的地方可以直接在邮箱lucky_glass@foxmail.com email我,在周末我会尽量解答并完善博客~)