◇例题·I◇ Snuke's Subway Trip
题目来源:Atcoder Regular 061 E题(beta版) +传送门+
一、解析
(1)最短路实现
由于在同一家公司的铁路上移动是不花费的,只有在换乘时会花费1日元。我们可以视换乘的花费为点权——当换乘到不同公司时花费1,同一家公司时花费0。
对于这种点权因情况而变化的题,最常见的做法便是拆点。设节点 u 相连的铁路由 c1,c2,...,cp p个公司修建,则将节点u拆分为节点 uc1~ucp,点uci表示到达点u的铁路是由公司ci修建的。若两点u,v被公司c修的铁路相连,则将 uc 与 vc 连接一条权为0的边——因为在同一家公司的铁路上移动无花费。
举个例子:
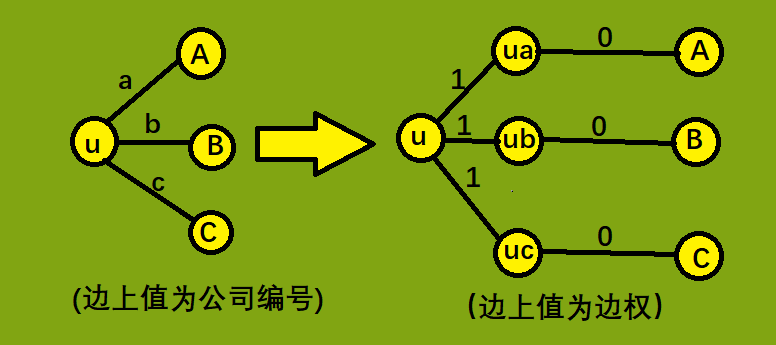
拆完点后SPFA跑一次最短路,最后答案要除以2。
为什么可以这样做呢?
如果只通过公司c的铁路能够从u到v(中途不转到其他公司的铁路),那么我们就能够从uc花费0日元移动到vc。
如果在节点u要从a公司转到b公司,我们需要通过 ua->u->ub。如何理解这一过程呢?我们可以把u看成一个站点——你到达u时在公司a的站台上,然后你需要花费1日元回到站点u,然后通过站点u中转,再花费1日元到达公司b的站台。但是我们会发现,题目要求是换乘只需要1日元,而我的程序每换乘一次需要2日元,就会比正确答案大一倍,所以最后要除以2。
可能不太清楚,看个例子
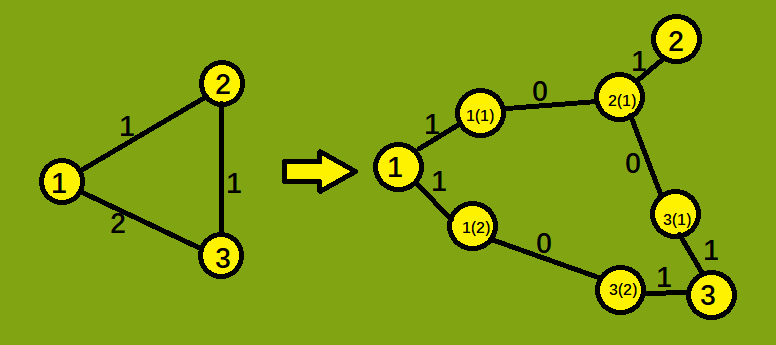
(我觉得我好像讲的不大清楚,reader们不懂的可以看文章底的邮箱问我 QwQ)
(2) 二分图实现
(其实我这种实现写TLE了……但是我知道有这种思路,于是写上了)
对于原图,我们定义可以通过同一家公司的铁路到达的点集为一个连通块,也就是说在同一个连通块内的所有点互相可以到达,且经过的铁路是同一家公司的(花费为0),而不同的连通块的点互相到达需要花费。
由于一个连通块的点之间花费为0,我们可以把每个连通块都缩成一个点x,把该连通块内的点与x连接。然后我们会发现这样构成的图形成了一个二分图,X部为原图的点,Y部为连通块缩成的点。再用BFS从原图的点1(起点)到原图的点n(终点)搜索一遍求得1到n的最短路,把所得解除以2就是答案。
(同样的问题)为什么可以这么做呢?
可以把X部看成中转站,而Y部为铁路。因为连通块内的点可以互相到达,我们把从中转站进入铁路的花费和从铁路出到中转站的花费都设为1,那么同一个连通块内的两个点u,v的最小花费路径则是从u出发经过连通块内的其他点到达v,花费为0。同样,从点1到点n的路径可以看成从1出发经过若干个连通块到达n。我们可以证明——从1到n的最短路径经过同一个连通块的次数不超过1——设最短路径进入某一个连通块时点为u,而从该连通块离开的点为v,一定存在一条花费为0的从u到v的路径(因为他们在一个连通块内嘛),而如果从u出发,经过其他连通块再到达v,则花费一定大于0,因此经过该连通块的次数一定不超过1。
其实不难发现,u到v的最小花费就是u到v的最短路径中经过的连通块的个数(看下面的例子),而且u到v的路径在二分图中一定是“u->连通块1->中转站1->...->中转站k->连通块k->v(k就是答案)”,在二分图中形成k个“V”形,即经过边数为 2k 条。所以答案(k)就是经过边数除以2。
二、实现
就只讲一下那些比较难写的地方,简单的步骤就默认大家会了……
(1)最短路拆点 - map储存编号(ID)
这一步可以在线处理。对于点u储存一个map<int,int>ID[u],ID[u][c]表示u的由c公司修的铁路所拆分的虚拟节点的编号。可以在读入边的时候处理——用map自带的函数count(c)判断端点u,v的映射(map)中是否存在公司c,如果没有,则给它赋一个值cnt。我们可以把虚拟节点的编号储存在原图节点的后面,即cnt从n+1开始。同时连接u,v关于c公司生成的两个虚拟节点 ID[u][c],ID[v][c]。
再枚举1~n的点,对于每一个点i,用迭代器枚举map。这里是一个技巧,大家可以看一看:
迭代器iterator——STL容器遍历利器
迭代器相当于一个指针,可以指向特定STL容器的元素。由于STL容器除了vector好像就没有可以直接访问、遍历元素(在不改变原容器的情况下)的容器了,遍历起来就比较麻烦。我们可以定义一个迭代器,map的格式就像这样 “map<类型,类型>::iterator”。迭代器本身是一个数据类型,若要遍历一个 map<int,int> ma ,迭代器就定义为 "map<int,int>::iterator it",用for循环枚举:“for(map<int,int>::iterator it=ma.begin();it!=ma.end();it++)” 。这里的"it++"是迭代器重定义了"++",指向容器的下一个元素。
map<>这种容器比较特别,它的元素其实是一个pair,其中pair的first是下标,second是下标对应的值。注意用迭代器访问元素时,迭代器类似于指针,所以访问first,second时是用指针的"->"而不是结构体的"."。
这里的second就是该虚拟节点对应的ID,直接将该虚拟节点与节点i连边即可。
for(int i=0;i<n_edg;i++)
{
int u,v,c;scanf("%d%d%d",&u,&v,&c); //读边
input[i][0]=u;input[i][1]=v;input[i][2]=c;
if(!ID[u].count(c)) ID[u][c]=cnt++; //存虚拟节点id
if(!ID[v].count(c)) ID[v][c]=cnt++;
lnk[ID[u][c]].push_back(make_pair(ID[v][c],0)); //连接两个虚拟节点
lnk[ID[v][c]].push_back(make_pair(ID[u][c],0));
}
for(int i=1;i<=n_pnt;i++) //枚举原图点
for(map<int,int>::iterator it=ID[i].begin();it!=ID[i].end();it++) //枚举虚拟点
{
int id=it->second; //id是虚拟节点的编号
lnk[i].push_back(make_pair(id,1)); //连接原图点与虚拟节点
lnk[id].push_back(make_pair(i,1));
}
(2)二分图改造 - 原图与二分图的转换(我觉得就是这里TLE了)
先用vector<>邻接表储存原图 fir_lnk,再用map<int,bool> cpn[],cpn[u][k]表示与节点u连接的铁路是否有k公司修的,即属于公司k的铁路连通块是否包含u。
枚举点 1~n,再用迭代器枚举公司,如果节点 i 与公司 j 的连通块还没有被枚举到,则用 BFS(Linker) 遍历该连通块,遍历到一个点后清除该点与连通块的标记,同时连接点与连通块(构造二分图)。
Linker:
void Linker(int start,int edge,int ID)
{
queue<int> que;
que.push(start);
while(!que.empty())
{
int u=que.front();que.pop();
lnk[u].push_back(ID); //构造二分图
lnk[ID].push_back(u);
for(int i=0;i<fir_lnk[u].size();i++)
if(fir_lnk[u][i].second==edge)
{
int v=fir_lnk[u][i].first;
if(!cpn[v][edge]) continue;
cpn[v][edge]=false; //清除标记
que.push(v);
}
}
}
枚举:
for(int i=1;i<=n_pnt;i++) //枚举点
for(map<int,bool>::iterator it=cpn[i].begin();it!=cpn[i].end();it++) //枚举连通块
if(it->second)
Linker(i,it->first,cnt++); //BFS
三、源代码
(最短路 AC)

1 /*Lucky_Glass*/ 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<iostream> 6 #include<map> 7 #include<vector> 8 #include<queue> 9 using namespace std; 10 const int MAXN=(int)1e5; 11 const int INF=(int)1e9; 12 int n_pnt,n_edg,cnt; 13 map<int,int> ID[MAXN+5]; 14 int input[2*MAXN+5][3]; 15 vector<pair<int,int> > lnk[5*MAXN+5]; 16 int dist[5*MAXN+5]; 17 bool vis[5*MAXN+5]; 18 int main() 19 { 20 scanf("%d%d",&n_pnt,&n_edg); 21 cnt=n_pnt+1; 22 for(int i=0;i<n_edg;i++) 23 { 24 int u,v,c;scanf("%d%d%d",&u,&v,&c); 25 input[i][0]=u;input[i][1]=v;input[i][2]=c; 26 if(!ID[u].count(c)) ID[u][c]=cnt++; 27 if(!ID[v].count(c)) ID[v][c]=cnt++; 28 lnk[ID[u][c]].push_back(make_pair(ID[v][c],0)); 29 lnk[ID[v][c]].push_back(make_pair(ID[u][c],0)); 30 } 31 for(int i=1;i<=n_pnt;i++) 32 for(map<int,int>::iterator it=ID[i].begin();it!=ID[i].end();it++) 33 { 34 int id=it->second; 35 lnk[i].push_back(make_pair(id,1)); 36 lnk[id].push_back(make_pair(i,1)); 37 } 38 fill(dist,dist+5*MAXN+5,INF); 39 dist[1]=0;vis[1]=true; 40 queue<int> que;que.push(1); 41 while(!que.empty()) 42 { 43 int u=que.front();que.pop(); 44 for(int i=0;i<lnk[u].size();i++) 45 { 46 int v=lnk[u][i].first,l=lnk[u][i].second; 47 if(dist[v]>dist[u]+l) 48 { 49 dist[v]=dist[u]+l; 50 if(!vis[v]) 51 vis[v]=true,que.push(v); 52 } 53 } 54 vis[u]=false; 55 } 56 if(dist[n_pnt]==INF) printf("%d ",-1); 57 else printf("%d ",dist[n_pnt]/2); 58 return 0; 59 }
(二分图 TLE)

1 /*Lucky_Glass*/ 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<vector> 6 #include<queue> 7 #include<map> 8 using namespace std; 9 int n_pnt,n_edg,cnt; 10 const int MAXN=int(3e5); 11 vector<int> lnk[MAXN+5]; 12 vector<pair<int,int> > fir_lnk[int(1e5)+5]; 13 map<int,bool> cpn[int(1e5)+5]; 14 bool vis[MAXN+5],fir_vis[int(1e5)+5]; 15 void Linker(int start,int edge,int ID) 16 { 17 queue<int> que; 18 que.push(start); 19 while(!que.empty()) 20 { 21 int u=que.front();que.pop(); 22 lnk[u].push_back(ID); 23 lnk[ID].push_back(u); 24 for(int i=0;i<fir_lnk[u].size();i++) 25 if(fir_lnk[u][i].second==edge) 26 { 27 int v=fir_lnk[u][i].first; 28 if(!cpn[v][edge]) continue; 29 cpn[v][edge]=false; 30 que.push(v); 31 } 32 } 33 } 34 int main() 35 { 36 scanf("%d%d",&n_pnt,&n_edg); 37 cnt=n_pnt+1; 38 for(int i=0;i<n_edg;i++) 39 { 40 int u,v,c; 41 scanf("%d%d%d",&u,&v,&c); 42 fir_lnk[u].push_back(make_pair(v,c)); 43 fir_lnk[v].push_back(make_pair(u,c)); 44 cpn[u][c]=cpn[v][c]=true; 45 } 46 for(int i=1;i<=n_pnt;i++) 47 for(map<int,bool>::iterator it=cpn[i].begin();it!=cpn[i].end();it++) 48 if(it->second) 49 Linker(i,it->first,cnt++); 50 queue<pair<int,int> > que; 51 que.push(make_pair(1,0)); 52 while(!que.empty()) 53 { 54 pair<int,int> fro=que.front();que.pop(); 55 int u=fro.first,stp=fro.second; 56 for(int i=0;i<lnk[u].size();i++) 57 { 58 int v=lnk[u][i],fstp=stp+1; 59 if(vis[v]) continue; 60 vis[v]=true; 61 if(v==n_pnt) {printf("%d ",fstp/2);return 0;} 62 que.push(make_pair(v,fstp)); 63 } 64 } 65 printf("-1 "); 66 return 0; 67 }
The End
Thanks for reading!
- Lucky_Glass
(Tab:如果我有没讲清楚的地方可以直接在邮箱lucky_glass@foxmail.com email我,在周末我会尽量解答并完善博客~)
