【模板时间】◆模板·III◆ 单调子序列

◆模板·III◆ 单调子序列

以前只知道DP用 O(n²) 的做法，现在才发现求单调子序列方法好多……

---

◇ 模板简述

单调子序列包括 升序/降序/非升序/非降序 子序列。主要题型如下：

①在原串中找到一个最长的单调子序列；

②将原串分解为若干个单调子序列；

③通过修改元素使原串变为单调序列。

Tab: 子序列在原串中可以断开，也就是说若原串为A{a[1]~a[n]}，则其子序列可以是 A'{a[b[1]]~a[b[n]]}满足 b[1]<b[2]<...<b[n]

方法的确很多，包括STL(lower_bound)，DP……接着讲吧……

---

◇ 求原串中最长的单调子序列

【OpenJudge 1759】 +传送门+

一道非常经典的模板题——最长上升子序列。由于n最大1000，O(n²) 的算法是可以通过的。

解决这类问题的基础算法是DP。对于第i个数，我们可以找到一条以 i 结尾的上升子序列，记以 i 结尾的最长上升子序列的长度为 dp[i]，也就是我们的DP状态。

如何转移？

对于第 i 个数，若存在第j个数(j<i)小于第i个数，则第i个数可以继续连接在以j结尾的最长上升子序列上，因此转移可以写成下列：

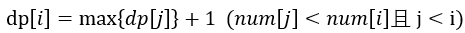
没有多大难度……其实只是数据规模不算大！

先附上代码（一个在 n≤3000 的情况下不会超时的版）：

/*Lucky_Glass*/
#include<cstdio>
#include<algorithm>
using namespace std;
int A[1005],dp[1005],n,ans=1;
int DP(int x)
{
    if(dp[x]) return dp[x];
    dp[x]=1; //只有 第i个元素 本身
    for(int i=0;i<x;i++)
        if(A[i]<A[x])
            dp[x]=max(dp[x],DP(i)+1);
    return dp[x];
}
int main()
{
    scanf("%d",&n);
    for(int i=0;i<n;i++) scanf("%d",&A[i]);
    dp[0]=1;
    for(int i=n-1;i>=1;i--) //枚举对于以每一个元素为结尾的序列
        ans=max(DP(i),ans);
    printf("%d
",ans);
    return 0;
}

难度↑【POJ 1631】Bridging signals +传送门+

只是数据规模上升到40000了……O(n²)算法会炸……我们需要一种比DP更优秀的算法（DP有时并不是最优算法）。

不难发现，我们有时会沿用上一个最长上升子序列的前部分（也就是小于等于当前元素的最大元素的后面）。所以我们可以把以当前元素结尾的最长上升子序列给存下来（seq[]）。由于seq[]存储的是一个单调序列，所以我们可以在seq里二分查找(lower_bound)！

具体怎么做？

先初始化seq的所有值为正无穷（memset(seq,0x3f,sizeof seq)），这样才能在第一次查找时找到seq[1]。

若当前要求以num[i]结尾的最长上升子序列。先通过lower_bound找到seq[1~n-1]中小于等于num[i]的元素 seq[pos-1] （如果找不到此元素，则应找到seq[1]），然后将 seq[pos] 替换为num[i]，此时seq[1~pos]则是以 num[i] 结尾的最长上升子序列，且序列长度为 pos，此时就可以更新答案了。

/*Lucky_Glass*/
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int MAXN=40000;
int num[MAXN+5],seq[MAXN+5];
int main()
{
    int T;scanf("%d",&T);
    while(T--)
    {
        int n;scanf("%d",&n);
        for(int i=0;i<n;i++) scanf("%d",&num[i]);
        memset(seq,0x3f,sizeof seq); //初始化为正无穷
        int ans=0;
        for(int i=0;i<n;i++)
        {
            int pos=lower_bound(seq+1,seq+n,num[i])-seq; //pos-1是小于等于num[i]的最大元素
            seq[pos]=num[i]; //更新序列
            ans=max(ans,pos); //更新答案
        }
        printf("%d
",ans);
    }
    return 0;
}

---

◇ 通过修改原串元素形成单调序列

【Codeforces 13C】Sequence +传送门+

将元素ｉ从ａ改成ｂ的花费为 |a-b| ，现给出一个序列，修改一些元素，使得序列形成单调序列（不下降/不上升），求最小花费。

一个简单结论：对于每一个数，修改其值为先前的数或不修改，一定可以使原串形成单调序列。

于是我们定义dp[i][j]为第i个数值为j时的最小花费。

从小到大枚举i先前的每一个数值（包括i，此时相当于不修改）j，表示第i个数将修改为j，则花费为|j-num[i]|。由于我们是从小到大枚举的值，我们可以储存Min，表示dp[i-1][1~j]中最小的值，以此更新dp[i][j]，也就是说：

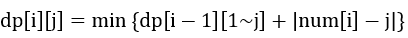
但是我们发现j太大了（1e9），存不下，于是可以用离散化来优化一下……最坏情况下，原序列每一个元素都不相等，第二维为5000，仍然存不下。回过头看我们的转移式，我们其实只需要用到dp[i-1]，所以我们只需要滚动数组就可以了。

/*Lucky_Glass*/
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<vector>
#include<cmath>
using namespace std;
const int MAXN=5000;
typedef long long ll;
int n;
int hgt[MAXN+5],fhgt[MAXN+5];
vector<int> uni;
ll dp[2][MAXN+5];
int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
        scanf("%d",&hgt[i]),uni.push_back(hgt[i]);
    sort(uni.begin(),uni.end());
    uni.erase(unique(uni.begin(),uni.end()),uni.end()); //离散化
    ll ans=ll(1e16);
    for(int i=1;i<=n;i++)
    {
        ll Min=ll(1e16);
        for(int j=0;j<uni.size();j++)
        {
            Min=min((ll)Min,dp[(i-1)%2][j]); //取1~j的最小值
            dp[i%2][j]=Min+fabs(1.0*hgt[i]-uni[j]);  //%2 滚动数组
            if(i==n) ans=min(ans,dp[i%2][j]); //更新答案
        }
    }
    printf("%lld
",ans);
    return 0;
}

---

 (Tab：以上每一篇代码都是模板，可以直接套上用的~) 

The End

Thanks for reading!

- Lucky_Glass

（Tab：如果我有没讲清楚的地方可以直接在邮箱lucky_glass@foxmail.com email我，在周末我会尽量解答并完善博客~）