opengl 计算机图形学 第三版 第二部分 第三章更多的绘图工具
3.1 概述
第2章中 我们绘图使用的是屏幕窗口的基础坐标系 以像素为单位
屏幕坐标从左下角x从0延伸到screenWidth-1 y从0向上延伸到screenHeight-1 只能使用非负的x和y
程序中用于描述对象几何信息 此过程为建模任务
在屏幕中如何将这个对象 按照一定比例显示出来 是一个观看的任务
使用最适合与手中问题的坐标系来描述对象,并且可以自动的缩放和平移图片,使得其能正确地在屏幕窗口中显示,这个描述对象的空间被称为世界坐标系(场景中的物体在实际世界中的坐标)。在合适的单位下,它就是数学中常用的笛卡尔xy坐标系。
世界窗口:在世界坐标系中定义一个对齐的矩形 (矩形的边与坐标轴平行) 不一定是屏幕
世界窗口指明了要绘制世界的哪一部分。对此可以理解为,任何在窗口中的部分需要被绘制,而窗口外的部分被裁减并不被绘制。 opengl会自动的裁减。
显示器的屏幕窗口上定义一个对齐的矩形的视口,不同于世界窗口 opengl会自动建立世界窗口和视口的变换(包括缩放和平移)。
对象在世界窗口中显示的部分会被自动的映射到视口中,也就是被映射到屏幕坐标中。
对齐的矩形作为窗口和视口(屏幕窗口)的形状原因:
1.矩形仅需要四个参数描述
2.检测一个点的位置(窗口内外) 很容易,可以简化裁减算法。
3.对齐的矩形为凸 简化绘制算法
4.通过一个窗口取看被绘制的物体, 并价格窗口中可见的快照放到显示器的视口中
采用窗口/视口的联合方式, 当两个口被指定时,coder可以编写一个算法,不考虑图片的大小和位置,所有潜在的操作(缩放、位置和裁减)都会自动完成,并将图片放到视口中去。
3.2世界窗口和视口
创建一个函数图像之后,并不知道 图像的位置和图像的大小,所以使用世界窗口就非常的重要
setWindow()用来建立世界窗口
setViewport()来建立视口
代码中涉及的坐标是在自然坐标系中操作的 例如x在-4.0~4.0 变化的 关键问题是如何缩放和平移不同的(x,y) 使得图像能在屏幕窗口中恰当的显示。
通过设置一个世界窗口和一个视口,并建立它们之间的一个合适的映射,就可以完成适当的平移和缩放。视口和窗口是coder 指定的对齐的矩形。
窗口为世界坐标系中
视口为屏幕窗口的一部分。

前者为世界窗口;后者为在屏幕中划出一部分区域为屏幕窗口,在其中再画出一部分为视口。
3.2.1 窗口到视口的映射
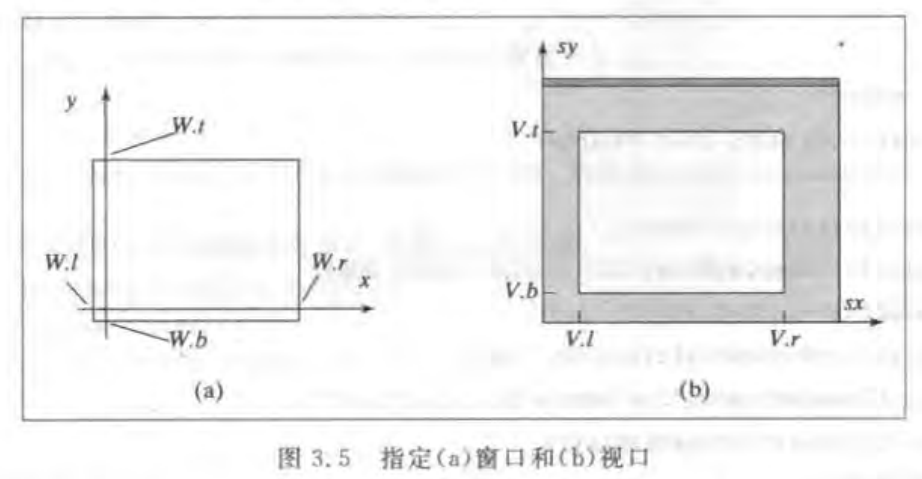
图中的w和v都是GLfloat类型的数值,代表作标值,其中left 和right为x轴的值 、 bottom和top为y轴的值,综合到一起成为了对齐的矩形
世界窗口和视口 纵横比不一定一致 如果不一致会导致图像的拉伸,所以需要调整世界窗口和视口的纵横比一致
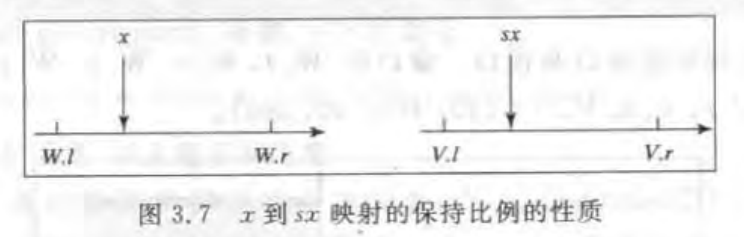
一个映射或者变换,即窗口到视口的映射,这个映射是基于一个等式,对每一个在世界坐标下的点(x,y),产生屏幕坐标系中的一个点(sx,sy)。
保持比例的性质 有下面的线性性质:
sx=A*x+C
sy=B*y+D
其中A、B、C、D是常数, A B缩放x和y的坐标 而 C D用来平移它们。
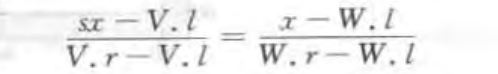

a 如果x是窗口的左边界 x=w.left 则sx为视口的左边界 sx=v.left
b 如果x是在窗口的右边界x=w.right,则sx是在视口的右边界 sx=v.right
c 对于某个比例f 如果x位于窗口的1/f处 则sx位于视口宽度的1/f处
d 如果x在窗口的左边界外 x<w.left 则sx也在视口的的左边界外 sx<v.left
设立窗口到视口的映射
opengl通过多个变换完成所需要的映射,自动的传送给定的每一个顶点 通过glVertex2*()命令
二维图形中,世界窗口由函数gluOrth2D()来设定 原型如下:
void gluOrtho2D(GLdouble left,GLdouble right,GLdouble bottom,GLdouble top);
三维的情况 还有另外两个参数需要设定 省略
视口的设定:
void glViewport(GLint x,GLint y,GLint width,GLint eight); 左下角的坐标以及宽度和高度
通过矩阵来完成所有的变换,因此gluOrtho2D()的调用必须在glMatrixModel(GL_PROJECTION)和glLoadIdentity()两个函数之后完成
所以建立窗口设视口之间的联系需要如下代码:
glMatrixModel(GL_PROJECTION;
glLoadIdentity();
gluOrtho2D(0.0,2.0,0.0,1.0); 设置窗口
glViewport(40,60,360,240); 设置视口
在此之后 每个使用glVertex2*(x,y)发送给opengl的点,会进行等式的映射,并且在窗口的边界处会被自动裁减掉边缘。
将设定窗口的函数放在setWindow()函数中 将glViewport() 放在setViewport函数中
void setWindow(GLdouble left,GLdouble right,GLdouble bottom,GLdouble top) 设置窗口
{
glMatrixModel(GL_PROJECTION);
glLoadIdentity();
gluOrtho2D(left,right,bottom,top);
}
void setViewport(GLint left,GLint right,GLint bottom,GLint top) 设置视口
{
glViewport(left,bottom,right-left,top-bottom);
}
(1)在main()中
glutInitWindowSize(640,480) 设置窗口大小
没有使用glViewport的命令 所以使用默认的视口,默认的视口就是整个屏幕窗口。
(2)在myInit()中
glMatrixModel(GL_PROJECTION);
glLoadIdentity();
gluOrtho2D(0.0,640.0,0.0,480.0); //关键的设置 与视口比较 以及纵横比
上面这些函数都是将世界窗口设置为对齐的矩形,其两个角的坐标是(0,0)和(640.0,480.0) 正好与视口的大小相等。
案例1:针对同一个图案,使用不同的视口,可以做到在屏幕窗口上的平铺
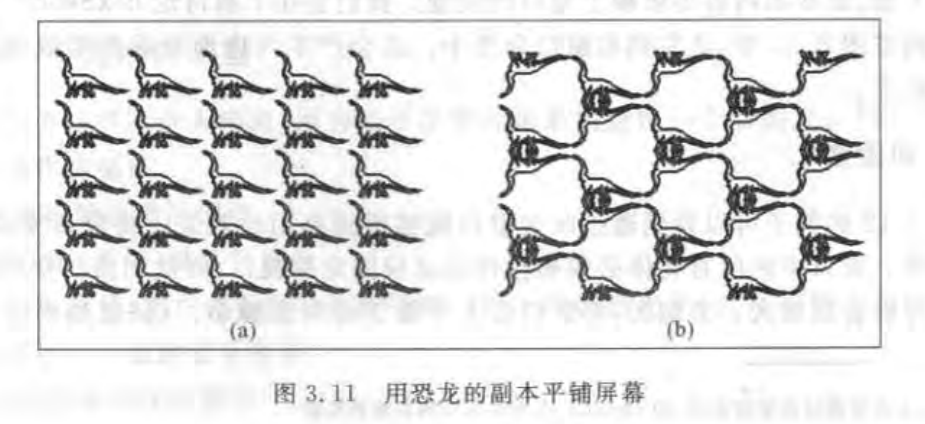
例如a所示的就是平铺
代码如下: 将恐龙替换成矩形 代码如下
setWindow(0,640.0,0,440.0) //设置窗口 for(int i=0,i<5;i++) //每列 { for(int j=0;j<5;j++) //每行 { glViewport(i*64,j*44,64,44) // 视口的移动方向先第0列 再第1列 ... drawPolylineFile("dino.dat");//在绘制一遍 } } 其中dino.dat为折线的文件
//折线恐龙 #include <windows.h> #include <gl/gl.h> #include <gl/glu.h> #include <gl/glut.h> #include <iostream> #include <math.h> using namespace std; const int screenWidth=250; const int screenHeight=250; void setWindow(GLdouble left,GLdouble right,GLdouble bottom,GLdouble top) //设置窗口 { gluOrtho2D(left,right,bottom,top);//窗口到视口的转换 } void setViewport(GLint left,GLint right,GLint bottom,GLint top) //设置视口 { glViewport(left,bottom,right-left,top-bottom); } void myInit(void) { glClearColor(1.0,1.0,1.0,0.0); //背景颜色 白色 最亮 glColor3f(0.0f,0.0f,0.0f); //线条颜色为黑色 glPointSize(10.0); //点像素大小 glMatrixMode(GL_PROJECTION); glLoadIdentity(); setWindow(0,60.0,0,60.0);//设置世界坐标系中的窗口 } void draw(void) //画图函数 { glBegin(GL_LINE_LOOP); //三角形的点 glVertex2i(10,10); glVertex2i(10,50); glVertex2i(50,50); glEnd(); } void myDisplay(void) //注册函数 { glClear(GL_COLOR_BUFFER_BIT); for(int i=0;i<5;i++) { for(int j=0;j<5;j++) { glViewport(i*50,j*50,50,50); //设置视口 draw(); } } glFlush(); } int main(int argc,char ** argv) { glutInit(&argc,argv); glutInitDisplayMode(GLUT_SINGLE|GLUT_RGB); glutInitWindowSize(screenWidth,screenHeight); glutInitWindowPosition(100,150); glutCreateWindow("折线矩形"); glutDisplayFunc(myDisplay); myInit(); glutMainLoop(); return 0; }
下图为执行效果图:

b图为交替倒置 产生的效果
判断i+j是偶数和奇数,然后倒转top和bottom的值 以实现视口的倒转
代码如下:
for(int i=0;i<5;i++)//列 { for(int j=0;j<5;j++)//行 { if((i+j)%2==0)//i+j是偶数 setWindow(0.0,640.0,0.0,440.0);//正常的世界窗口 else //i+j为奇数 setWindow(0.0,640.0,440.0,0.0);//颠倒的世界窗口 glViewport(i*64,j*44,64,44);//设置下一个视口 drawPloylineFile("dino.dat");//再次绘制 } }
完整代码如下
//折线恐龙 #include <windows.h> #include <gl/gl.h> #include <gl/glu.h> #include <gl/glut.h> #include <iostream> #include <math.h> using namespace std; const int screenWidth=250; const int screenHeight=250; void setWindow(GLdouble left,GLdouble right,GLdouble bottom,GLdouble top) //设置窗口 { glMatrixMode(GL_PROJECTION); //以下这两句一定要从myInit函数中抽出放到此位置 glLoadIdentity(); gluOrtho2D(left,right,bottom,top); //窗口到视口的转换 } void setViewport(GLint left,GLint right,GLint bottom,GLint top) //设置视口 { glViewport(left,bottom,right-left,top-bottom); } void myInit(void) { glClearColor(1.0,1.0,1.0,0.0); //背景颜色 白色 最亮 glColor3f(0.0f,0.0f,0.0f); //线条颜色为黑色 glPointSize(10.0); //点像素大小 } void draw(void) //画图函数 { glBegin(GL_LINE_LOOP); glVertex2i(10,10); glVertex2i(10,50); glVertex2i(50,50); glEnd(); } void myDisplay(void) //注册函数 { glClear(GL_COLOR_BUFFER_BIT); for(int i=0;i<5;i++) { for(int j=0;j<5;j++) { if((i+j)%2==0)//i+j是偶数 setWindow(0.0,60.0,0.0,60.0);//正常的世界窗口 else //i+j为奇数 setWindow(0.0,60.0,60.0,0.0);//颠倒的世界窗口 glViewport(i*50,j*50,50,50); //设置视口 draw(); } } glFlush(); } int main(int argc,char ** argv) { glutInit(&argc,argv); glutInitDisplayMode(GLUT_SINGLE|GLUT_RGB); glutInitWindowSize(screenWidth,screenHeight); glutInitWindowPosition(100,150); glutCreateWindow("折线矩形"); glutDisplayFunc(myDisplay); myInit(); glutMainLoop(); return 0; }
执行结果的图片

裁减图片的某部分
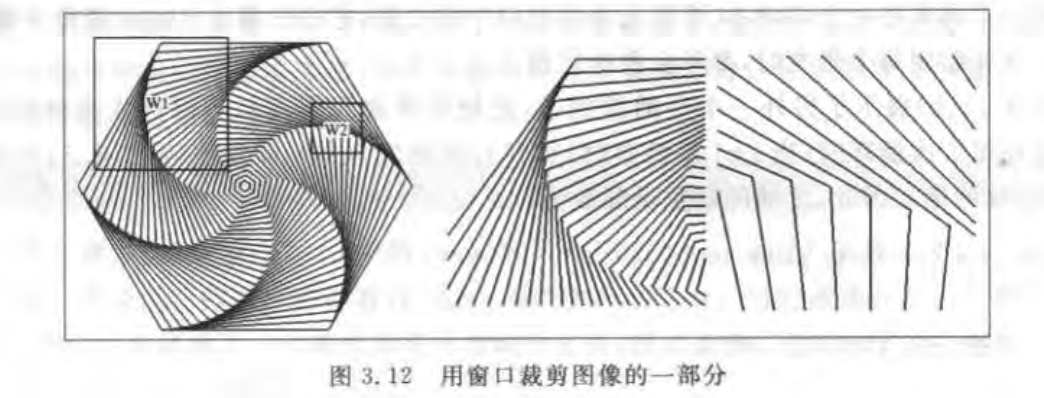
视口不变,改变世界窗口 用以显示不同的图案
上例中w1 和w2两个不同的窗口 视口不变,当使用w1时屏幕视口中显示的是w1中所裁切出的图案,而使用w2时则屏幕显示的是w2中裁切出的图案。
代码框架如下:
setWindow(...); //每张图片都改变窗口 setViewport(...); //每张图片使用同样的视口 hexSwirl(); //调用同样的画图函数
坐标系统绘制
//画笛卡尔坐标系 #include <windows.h> #include <gl/gl.h> #include <gl/glu.h> #include <gl/glut.h> #include <iostream> #include <math.h> using namespace std; const int screenWidth=1024; const int screenHeight=768; void setWindow(GLdouble left,GLdouble right,GLdouble bottom,GLdouble top) { glMatrixMode(GL_PROJECTION); glLoadIdentity(); gluOrtho2D(left,right,bottom,top); } void setViewport(GLint left,GLint right,GLint bottom,GLint top) { glViewport(left,bottom,right-left,top-bottom); } void drawpolygon(void) { setWindow(0,screenWidth,0,screenHeight); setViewport(0,screenWidth,0,screenHeight); glClear(GL_COLOR_BUFFER_BIT); glBegin(GL_POINTS); for(int x=0;x<=screenWidth;x++) glVertex2i(x,screenHeight/2); for(int y=0;y<=screenHeight;y++) glVertex2i(screenWidth/2,y); glEnd(); glFlush(); } void myInit(void) { glClearColor(1.0,1.0,1.0,0.0); glColor3f(0.0f,0.0f,0.0f); glPointSize(3.0); } int main(int argc,char ** argv) { glutInit(&argc,argv); glutInitDisplayMode(GLUT_SINGLE|GLUT_RGB); glutInitWindowSize(screenWidth,screenHeight); glutInitWindowPosition(100,150); glutCreateWindow("画坐标系"); glutDisplayFunc(drawpolygon); myInit(); glutMainLoop(); return 0; }
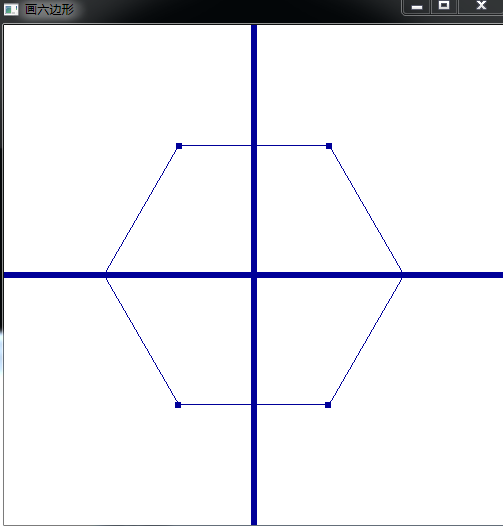
画六边形:
//画笛卡尔坐标系中的六边形 #include <windows.h> #include <gl/gl.h> #include <gl/glu.h> #include <gl/glut.h> #include <iostream> #include <math.h> using namespace std; typedef struct point{ GLdouble x; GLdouble y; }point; const int screenWidth=500; const int screenHeight=500; const int N=6; point sp[N]; point temp; //全局变量 double pi=3.1415926; double theta=2*pi/N; double r=150; void moveto(GLdouble x,GLdouble y) //设置当前的笔触到坐标点 { temp.x=x; temp.y=y; } void lineto(GLdouble x,GLdouble y)//从当前的点画线到指定的坐标点 两点间的连线 { glBegin(GL_LINES); glVertex2d(temp.x,temp.y); glVertex2d(x,y); glEnd(); //glFlush(); temp.x=x; //重新设置当前虚拟笔触的坐标值 temp.y=y; } void setWindow(GLdouble left,GLdouble right,GLdouble bottom,GLdouble top) //设置窗口 { glMatrixMode(GL_PROJECTION); glLoadIdentity(); gluOrtho2D(left,right,bottom,top); } void setViewport(GLint left,GLint right,GLint bottom,GLint top) //设置视口 { glViewport(left,bottom,right-left,top-bottom); } int drawpolygon(struct point p[],GLdouble theta,GLdouble r)//注意传递的参数 接收的参数 { setWindow(0,screenWidth,0,screenHeight); setViewport(0,screenWidth,0,screenHeight); glClear(GL_COLOR_BUFFER_BIT); glBegin(GL_POINTS); for(int x=0;x<=screenWidth;x++) //画坐标系 glVertex2i(x,screenHeight/2); for(int y=0;y<=screenHeight;y++) glVertex2i(screenWidth/2,y); for(int i=0;i<N;i++) { double x=r*cos(i*theta)+screenWidth/2; //计算六个点的坐标 并画出 double y=r*sin(i*theta)+screenHeight/2; glVertex2i(x,y); p[i].x=x; p[i].y=y; } glEnd(); for(int i=0;i<N;i++) //画线循环 { moveto(sp[i].x,sp[i].y); //利用全局变量 来画六边形 lineto(sp[(i+1)%6].x,sp[(i+1)%6].y);//取模算余数 } glFlush(); return 0; } void mydisplay(void) //注册的函数 { // drawpolygon(sp,theta,r); } void myInit(void) { glClearColor(1.0,1.0,1.0,0.0); glColor3f(0.0f,0.0f,0.6f); glPointSize(6.0); } int main(int argc,char ** argv) { glutInit(&argc,argv); glutInitDisplayMode(GLUT_SINGLE|GLUT_RGB); glutInitWindowSize(screenWidth,screenHeight); glutInitWindowPosition(100,150); glutCreateWindow("画六边形"); glutDisplayFunc(mydisplay); myInit(); glutMainLoop(); return 0; }
结果如下:
多个六边形
//多六边形 #include <windows.h> #include <gl/gl.h> #include <gl/glu.h> #include <gl/glut.h> #include <iostream> #include <math.h> using namespace std; typedef struct point{ GLdouble x; GLdouble y; }point; const int screenWidth=500; const int screenHeight=500; const int N=6; point sp[N]; point temp; //全局变量 double pi=3.1415926; double theta=2*pi/N; double r=240; void moveto(GLdouble x,GLdouble y) //设置当前的笔触到坐标点 { temp.x=x; temp.y=y; } void lineto(GLdouble x,GLdouble y)//从当前的点画线到指定的坐标点 两点间的连线 { glBegin(GL_LINES); glVertex2d(temp.x,temp.y); glVertex2d(x,y); glEnd(); //glFlush(); temp.x=x; //重新设置当前虚拟笔触的坐标值 temp.y=y; } void setWindow(GLdouble left,GLdouble right,GLdouble bottom,GLdouble top) //设置窗口 { glMatrixMode(GL_PROJECTION); glLoadIdentity(); gluOrtho2D(left,right,bottom,top); } void setViewport(GLint left,GLint right,GLint bottom,GLint top) //设置视口 { glViewport(left,bottom,right-left,top-bottom); } int drawpolygon(struct point p[],GLdouble tempt,GLdouble tempr)//注意传递的参数 接收的参数 { //setWindow(0,screenWidth,0,screenHeight); //setViewport(0,200,0,200); glBegin(GL_POINTS); //for(int x=0;x<=screenWidth;x++) //画坐标系 //glVertex2i(x,screenHeight/2); //for(int y=0;y<=screenHeight;y++) //glVertex2i(screenWidth/2,y); for(int i=0;i<N;i++) { double x=tempr*cos(i*tempt)+screenWidth/2; //计算六个点的坐标 并画出 double y=tempr*sin(i*tempt)+screenHeight/2; glVertex2i(x,y); p[i].x=x; p[i].y=y; } glEnd(); for(int i=0;i<N;i++) //画线循环 { moveto(sp[i].x,sp[i].y); //利用全局变量 来画六边形 lineto(sp[(i+1)%6].x,sp[(i+1)%6].y);//取模算余数 } // for(int j=0;j<N;j++) return 0; } void mydisplay(void) //注册的函数 { glClear(GL_COLOR_BUFFER_BIT); setWindow(0,screenWidth,0,screenHeight); setViewport(0,screenWidth,0,screenHeight); while(r>0) //循环画六边形 drawpolygon(sp,theta,r-=10); glFlush(); cout<<sp[1].x<<endl; } void myInit(void) { glClearColor(1.0,1.0,1.0,0.0); glColor3f(0.0f,0.0f,0.6f); glPointSize(3.0); } int main(int argc,char ** argv) { glutInit(&argc,argv); glutInitDisplayMode(GLUT_SINGLE|GLUT_RGB); glutInitWindowSize(screenWidth,screenHeight); glutInitWindowPosition(100,150); glutCreateWindow("画六边形"); glutDisplayFunc(mydisplay); myInit(); glutMainLoop(); return 0; }
结果:

缩放和漫游
将窗口变小则用于放大对象 相反窗口变大 相当于对象缩小。
有时候漫游也叫全视
在动画中放大图片
同心的多个窗口 固定的纵横比 窗口逐渐缩小 形成动画,每个窗口中显示的图片都是一帧 此过程类似与放大图像
绘制每一帧 都需要清一次屏幕 同时窗口越来越小 代码如下:
动画1:
float cx=0.3,cy=0.2;//窗口中心 float H,W=1.2, aspect=0.7;//窗口性质 set the viewport //设置视口 for(int frame=0;frame<NumFrames;frame++)//循环显示每一帧图像 { clear the screen //每次循环都清除之前的图案 W*=0.7; H=W*aspect; //保持纵横比 setWindow(cx-W,cx+W,cy-H,cy+H);//设置下一个窗口 hexSwirl(); }
动画2:
动画1的方式存在的问题
过程如下:
迅速擦除当前的图像;然后新图像被缓慢的重绘,因为仅仅有一个图像的缓存
解决上面问题的方法就是在用户浏览当前图像时,在一个“屏幕外内存”的地方绘制新的图像,然后将新图像显示在显示器上。
opengl提供了双缓存来完成任务,使用一个内存来模拟一个额外的屏幕,这个屏幕不显示在真实的显示器上,并所有的绘制都在这个缓存中进行。之后glutSwapBuufers()函数会将缓存中的图片转移到屏幕窗口上。
设置单缓存:glutInitDisplayModel(GLUT_SINGLE | GLUT_RGB);
设置成双缓存:glutInitDisplayModel(GLUT_DOUBLE | GLUT_RGB);
练习:3.2.2回旋的旋涡
3.3 裁减线
图形学中的基本任务,用于保持对象在给定的区域外的部分不被绘制
opengl环境中,每个对象都会被一个特殊的算法,自动的裁减到世界窗口 裁减器
3.3.1裁减一条线
cohen-sutherland 裁减器 计算p1和p2两个端点的线段的哪一部分位于世界窗口之内,并返回位于世界窗口内的部分的端点
函数 int clipSegment(Point2& p1,Point2& p2,RealRect window) 参数为两个二维的点以及一个对齐的矩形
功能为将p1和p2为端点的线段裁减到窗口边界处。如果线段的某一部分位于窗口内,则将新的端点存放在p1 和p2中,并且函数返回1,说明线段的某些部分是可见的。如果这条线温泉被裁减掉了,函数返回0,说明没有任何部分可见。
案例1:

典型的裁减器的情况 : clipsegment()函数对每条线段执行下列事件中的一件。
1.如果整条线段都在窗口内(例如线段cd) 函数返回1
2.整条线段在窗口外 例如线段AB 函数返回0
3.一个端点在窗口外,一个在窗口内 例如ED 函数将一个端点裁减 设置新的端点 然后返回1
4.两个端点都在窗口外, 但是此线段的一部分位于窗口内 例如线段AE 函数将裁减两个端点 并返回1
还有可能线段位于窗口的左侧 右侧 上面或者下面等等。
为了判断线段的位置 并且做出相应的裁减 cohen-sutherland提供了一个快速的分治算法。
3.3.2 cohen-sutherland裁减算法
平凡接受和平凡拒绝两种常见情况

图中的AB整个线段位于窗口内 因此AB被平凡的接受,而不需要裁减, 窗口很大时,大部分情况都是平凡接受。
图中CD整个线段 两个端点都位于W的另一条边外,则线段CD整个都在窗口外 此时CD就是平凡的拒绝。 窗口很小时,大部分情况都是平凡拒绝。
检测平凡接受或者平凡拒绝
仅仅检测端点即可

对线段的每一个端点计算一个“窗口内部/外部编码”,用于后续的测试。
四个编码的位置信息从左到右分别为 left above right below 分别代表 在左面 上面 下面 右面;
t代表true f代表false
如果点在窗口内部,则编码表示为FFFF;
下图为点与窗口的位置关系 的9种可能性
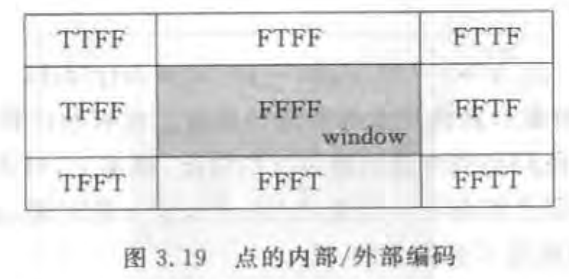
平凡接受:两个码字都是FFFF;
平凡拒绝:两个码字在某一位元素上都是T 两个点都是在窗口左边,或者都在它上面,等等
使用c/c++的位操作函数 可以实现码字的计算和测试。
没有平凡接受和拒绝时的截断
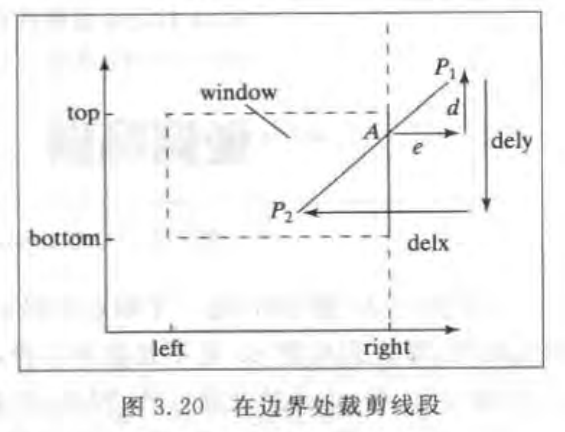
如果没有平凡接受或者拒绝时,此线段一定会被某个边界分成两个部分
do
{
设置p1 和p2的码字;
if(平凡接受) return 1;
if(平凡拒绝) return 0;
将线段在下一个窗口边界处截断;(重新设置p1或p2端点的位置)丢掉外面的部分;
}while(1);
最多四次循环就会终止,针对每个点 对齐矩形的四条边都会进行检测 所以需要四次循环。也就会出现平凡接受或者平凡拒绝的情况。

已知:p1和p2的坐标x和y w.right
未知:A点的x=w.right y=p1.y-d
d/dely=e/delx
delx=p2.x-p1.x;.........1
dely=p2.y-p1.y;........2
e=p1.x-w.right;.........3
由1 2 3可以计算出d的值 由此就可以计算出A点的y值
所以新p1.y (点A)
p1.y+=(w.right-p1.x)*dely/delx
剩余的窗口的三个边界的裁减方法类似。
对于水平的线 dely=0 ;对于垂直的线 delx=0; 分母为0的情况不会发生
伪代码2:
int clipSegment(Point & p1,Point2& p2,RealRect W) { do{ if(平凡接受) return 1; if(平凡拒绝) return 0; if(p1在窗口外面) { if(p1在窗口左边) 用左边界截断,更新p1; else if(p1在窗口右边) 用右边界截断,更新p1; else if(p1在窗口下面) 用下边界截断,更新p1; else if(p1在窗口上面) 用上边界截断,更新p1; } else //p2在窗口外面 { if(p2在窗口左边) 用左边界截断,更新p2; else if(p2在窗口右边) 用右边界截断,更新p2; else if(p2在窗口下面) 用下边界截断,更新p2; else if(p2在窗口上面) 用上边界截断,更新p2; } }while(1); }
每次执行循环时,每个端点的码字都会被重新计算和测试,每次都会对平凡接受和拒绝进行检测 ,如果失败,算法会检测p1是否在窗口外,如果p1在窗口内,那么p2一定在窗口外,针对在窗口外的点进行按边裁减。
裁减的顺序为左,右,下,上。
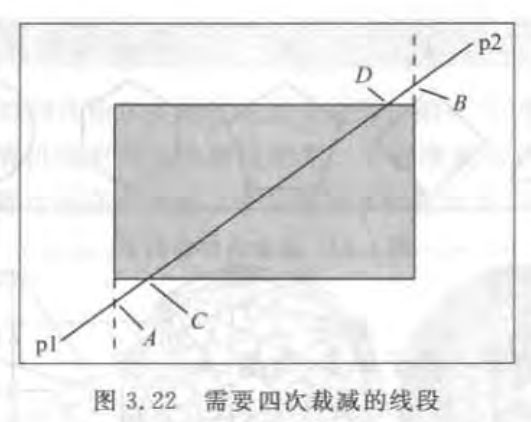
第一次:p1变为A
第二次:p2变为B
第三次:A变为C
第四次: B变为D
练习:3.3.1 手工模拟clipSegment (略)
3.3.2 除以0的情况永远不会发生。
3.4正多边形、圆和圆弧
3.4.1正多边形
所有边相等 内角相等 且边只能在端点处接触,称n条边的正多边形为正n边形。顶点等距离排放

半径为R的外接圆的圆心位于远点,而第一个点p0位于x轴的正方向,其它的顶点位于下面等式指定的位置:pi=(R*cos(i*a),R*sin(i*a)), i=1,2...5
其中a=2π/6=π/3。
1.如果圆心的坐标为(x,y),只要在上式中坐标中分别加上x和y即可。
2.如果将正六边形缩放S倍,只需要将R乘上S。
3.旋转只需要在cos和sin函数的参数中增加A即可
3.4.2正n边形的变种
将正n边形中的各个顶点均相连 会得到花环
花环.cpp
//绘制sinc函数 #include <windows.h> #include <iostream> #include <math.h> #include <gl/GL.h> #include <gl/GLU.h> #include <gl/GLUT.h> class GLintPoint //点类 { public: GLint x,y; }; class Point2 //线段端点类 { public: float x,y; void set(float dx,float dy){x=dx;y=dy;} //内联函数 且重载 void set(Point2 &p){x=p.x;y=p.y;} //内联函数 重载 设置端点 Point2(float xx,float yy){x=xx,y=yy;} //构造函数 非默认 Point2(){x=y=0;} //默认构造函数 }; Point2 currPos; //定义两个端点类的对象 Point2 CP; void moveTo(Point2 p) //移动当前的虚拟笔触 到一个端点 { CP.set(p); //设置当前点的坐标 } void lineTo(Point2 p) //从当前点的位置cp 到参数给定的点划线 { glBegin(GL_LINES); glVertex2f(CP.x,CP.y); glVertex2f(p.x,p.y); glEnd(); glFlush(); CP.set(p); //***重新设置当前的点 cp } //myInit void myInit(void) //初始化 窗口的个参数 背景颜色 线条颜色 以及宽度等等 { glClear(GL_COLOR_BUFFER_BIT); glClearColor(1.0,1.0,1.0,0.0); glColor3f(0.0f,0.0f,1.0f); } void rosette(int N,float radius) //触发的画图函数 参数为点数 和 半径值 { Point2 * pointlist=new Point2[N]; //创建数组用来存储线段的端点 GLfloat theta=(2.0f*3.1415926536)/N; //360度除以点数 算出角度数 for(int c=0;c<N;c++) { pointlist[c].set(radius*sin(theta*c),radius*cos(theta*c));//计算每个点的x和y值 并且填入对象数组 } for(int i=0;i<N;i++)//将数组中的所有点都连接起来 { for(int j=0;j<N;j++) { moveTo(pointlist[i]); lineTo(pointlist[j]); } } } void render()//渲染 { glClear(GL_COLOR_BUFFER_BIT);//清除背景颜色 glViewport(10,10,600,600); //设置视口 ***** x,y width height rosette(10,.50f); //画图 实参传送 glFlush(); //传送给opengl } //main int main(int argc,char ** argv) { glutInit(&argc,argv); glutInitDisplayMode(GLUT_SINGLE|GLUT_RGB); glMatrixMode(GL_PROJECTION); glLoadIdentity(); glutInitWindowSize(600,600); glutCreateWindow("rosette"); glutDisplayFunc(render); myInit(); glutMainLoop(); return 0; }
特例: 5花环 的特性
体现很多黄金分割率φ
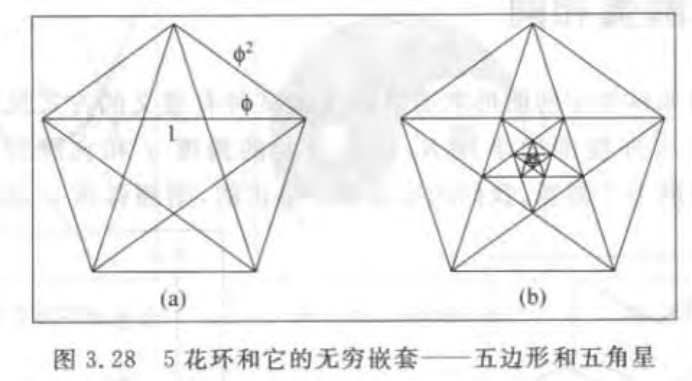
每条线段要比短于它的线段长φ倍,而且由于五角星的边又构成了一个内五边形,可以实现一个无穷的嵌套。
例子:3.4.2基于两个同心多边形的图形
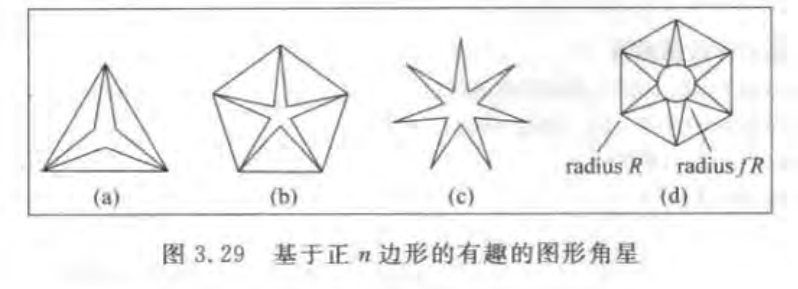
外半径是R,内半径是fR ,f是某个因子。每个图都使用了一个正n边形的变种,其半径在内径和外径之间交替。
图3.29a 代码示例:
//3.2.9图a #include <windows.h> #include <gl/gl.h> #include <gl/glu.h> #include <gl/glut.h> #include <iostream> #include <math.h> using namespace std; const int N=6; const double pi=3.1415926; const double theta=2*pi/N; const double R=200; const double r=50; const double screenWidth=500; const double screenHeight=500; class point { public: GLdouble x; GLdouble y; void setp(GLdouble _x,GLdouble _y){x=_x;y=_y;}; }; point sp; void moveTo(GLdouble x,GLdouble y) { sp.setp(x,y); } void lineTo(GLdouble x,GLdouble y) { glBegin(GL_LINES); glVertex2d(sp.x,sp.y); glVertex2d(x,y); glEnd(); sp.x=x; sp.y=y; } void photo(void) { class point p1[6]; class point p2[6]; glClear(GL_COLOR_BUFFER_BIT); glBegin(GL_POINTS); for(int i=0;i<N;i++) { GLdouble Rx=R*cos(i*theta)+screenWidth/2; GLdouble Ry=R*sin(i*theta)+screenHeight/2; p1[i].x=Rx; p1[i].y=Ry; GLdouble rx=r*cos(i*theta)+screenWidth/2; GLdouble ry=r*sin(i*theta)+screenHeight/2; p2[i].x=rx; p2[i].y=ry; glVertex2d(p1[i].x,p1[i].y); glVertex2d(p2[i].x,p2[i].y); } glEnd(); for(int i=0;i<N;i+=2) { moveTo(p1[i].x,p1[i].y); lineTo(p1[(i+2)%N].x,p1[(i+2)%N].y); } for(int i=0;i<N;i+=2) { moveTo(p1[i].x,p1[i].y); lineTo(p2[(i+1)%N].x,p2[(i+1)%N].y); moveTo(p2[i+1].x,p2[i+1].y); lineTo(p1[(i+2)%N].x,p1[(i+2)%N].y); } glFlush(); } void myInit(void) { glClearColor(1.0,1.0,1.0,0.0); //background color glColor3f(0.0f,0.2f,0.6f); //point color glPointSize(3.0); glMatrixMode(GL_PROJECTION); glLoadIdentity(); gluOrtho2D(0.0,500,0.0,500); } int main(int argc,char ** argv) { glutInit(&argc,argv); glutInitDisplayMode(GLUT_SINGLE|GLUT_RGB); glutInitWindowPosition(0,0); glutInitWindowSize(500,500); glutCreateWindow("内外圆多边形"); glutDisplayFunc(photo); myInit(); glutMainLoop(); return 0; }
结果
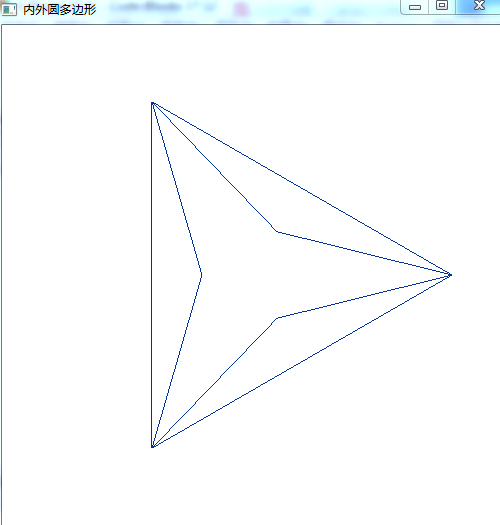
3.2.9图B 仅将a图代码中的N改为10即可
//3.2.9图b #include <windows.h> #include <gl/gl.h> #include <gl/glu.h> #include <gl/glut.h> #include <iostream> #include <math.h> using namespace std; const int N=10; const double pi=3.1415926; const double theta=2*pi/N; const double R=200; const double r=50; const double screenWidth=500; const double screenHeight=500; class point { public: GLdouble x; GLdouble y; void setp(GLdouble _x,GLdouble _y){x=_x;y=_y;}; }; point sp; void moveTo(GLdouble x,GLdouble y) { sp.setp(x,y); } void lineTo(GLdouble x,GLdouble y) { glBegin(GL_LINES); glVertex2d(sp.x,sp.y); glVertex2d(x,y); glEnd(); sp.x=x; sp.y=y; } void photo(void) { class point p1[N]; class point p2[N]; glClear(GL_COLOR_BUFFER_BIT); glBegin(GL_POINTS); for(int i=0;i<N;i++) { GLdouble Rx=R*cos(i*theta)+screenWidth/2; GLdouble Ry=R*sin(i*theta)+screenHeight/2; p1[i].x=Rx; p1[i].y=Ry; GLdouble rx=r*cos(i*theta)+screenWidth/2; GLdouble ry=r*sin(i*theta)+screenHeight/2; p2[i].x=rx; p2[i].y=ry; glVertex2d(p1[i].x,p1[i].y); glVertex2d(p2[i].x,p2[i].y); } glEnd(); for(int i=0;i<N;i+=2) { moveTo(p1[i].x,p1[i].y); lineTo(p1[(i+2)%N].x,p1[(i+2)%N].y); } for(int i=0;i<N;i+=2) { moveTo(p1[i].x,p1[i].y); lineTo(p2[(i+1)%N].x,p2[(i+1)%N].y); moveTo(p2[i+1].x,p2[i+1].y); lineTo(p1[(i+2)%N].x,p1[(i+2)%N].y); } glFlush(); } void myInit(void) { glClearColor(1.0,1.0,1.0,0.0); //background color glColor3f(0.0f,0.2f,0.6f); //point color glPointSize(3.0); glMatrixMode(GL_PROJECTION); glLoadIdentity(); gluOrtho2D(0.0,500,0.0,500); } int main(int argc,char ** argv) { glutInit(&argc,argv); glutInitDisplayMode(GLUT_SINGLE|GLUT_RGB); glutInitWindowPosition(0,0); glutInitWindowSize(500,500); glutCreateWindow("内外圆多边形"); glutDisplayFunc(photo); myInit(); glutMainLoop(); return 0; }
代码结果
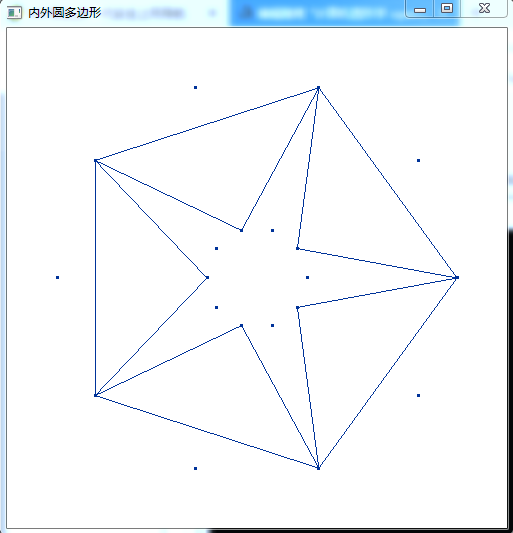
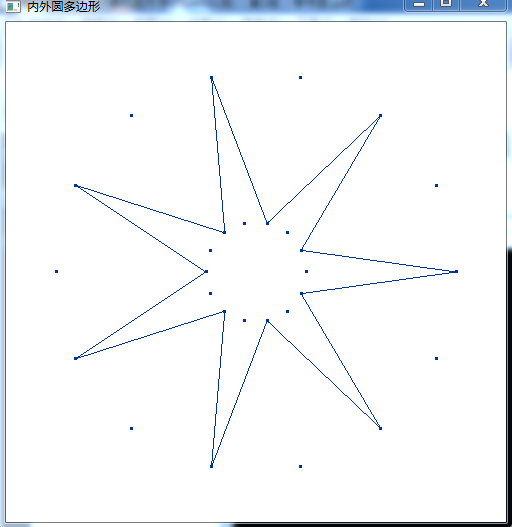
3.29图c 修改N 去掉外框线
//3.2.9图c #include <windows.h> #include <gl/gl.h> #include <gl/glu.h> #include <gl/glut.h> #include <iostream> #include <math.h> using namespace std; const int N=14; const double pi=3.1415926; const double theta=2*pi/N; const double R=200; const double r=50; const double screenWidth=500; const double screenHeight=500; class point { public: GLdouble x; GLdouble y; void setp(GLdouble _x,GLdouble _y){x=_x;y=_y;}; }; point sp; void moveTo(GLdouble x,GLdouble y) { sp.setp(x,y); } void lineTo(GLdouble x,GLdouble y) { glBegin(GL_LINES); glVertex2d(sp.x,sp.y); glVertex2d(x,y); glEnd(); sp.x=x; sp.y=y; } void photo(void) { class point p1[N]; class point p2[N]; glClear(GL_COLOR_BUFFER_BIT); glBegin(GL_POINTS); for(int i=0;i<N;i++) { GLdouble Rx=R*cos(i*theta)+screenWidth/2; GLdouble Ry=R*sin(i*theta)+screenHeight/2; p1[i].x=Rx; p1[i].y=Ry; GLdouble rx=r*cos(i*theta)+screenWidth/2; GLdouble ry=r*sin(i*theta)+screenHeight/2; p2[i].x=rx; p2[i].y=ry; glVertex2d(p1[i].x,p1[i].y); glVertex2d(p2[i].x,p2[i].y); } glEnd(); for(int i=0;i<N;i+=2) { moveTo(p1[i].x,p1[i].y); lineTo(p2[(i+1)%N].x,p2[(i+1)%N].y); moveTo(p2[i+1].x,p2[i+1].y); lineTo(p1[(i+2)%N].x,p1[(i+2)%N].y); } glFlush(); } void myInit(void) { glClearColor(1.0,1.0,1.0,0.0); //background color glColor3f(0.0f,0.2f,0.6f); //point color glPointSize(3.0); glMatrixMode(GL_PROJECTION); glLoadIdentity(); gluOrtho2D(0.0,500,0.0,500); } int main(int argc,char ** argv) { glutInit(&argc,argv); glutInitDisplayMode(GLUT_SINGLE|GLUT_RGB); glutInitWindowPosition(0,0); glutInitWindowSize(500,500); glutCreateWindow("内外圆多边形"); glutDisplayFunc(photo); myInit(); glutMainLoop(); return 0; }
结果图
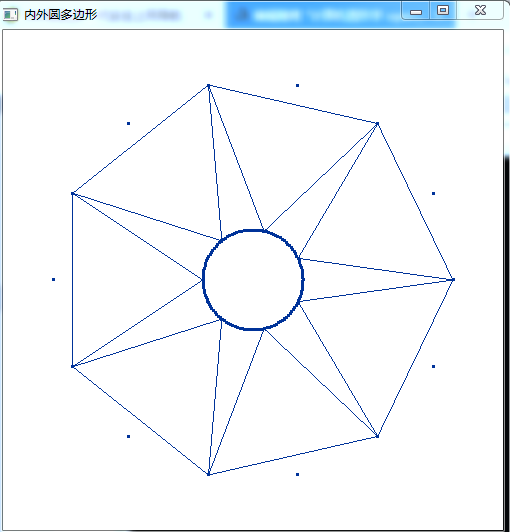
3.29图d 多加上一个画内圆的代码段
//3.2.9图c #include <windows.h> #include <gl/gl.h> #include <gl/glu.h> #include <gl/glut.h> #include <iostream> #include <math.h> using namespace std; const int N=14; const double pi=3.1415926; const double theta=2*pi/N; const double R=200; const double r=50; const double screenWidth=500; const double screenHeight=500; class point { public: GLdouble x; GLdouble y; void setp(GLdouble _x,GLdouble _y){x=_x;y=_y;}; }; point sp; void moveTo(GLdouble x,GLdouble y) { sp.setp(x,y); } void lineTo(GLdouble x,GLdouble y) { glBegin(GL_LINES); glVertex2d(sp.x,sp.y); glVertex2d(x,y); glEnd(); sp.x=x; sp.y=y; } void photo(void) { class point p1[N]; class point p2[N]; glClear(GL_COLOR_BUFFER_BIT); glBegin(GL_POINTS); for(int i=0;i<N;i++) { GLdouble Rx=R*cos(i*theta)+screenWidth/2; GLdouble Ry=R*sin(i*theta)+screenHeight/2; p1[i].x=Rx; p1[i].y=Ry; GLdouble rx=r*cos(i*theta)+screenWidth/2; GLdouble ry=r*sin(i*theta)+screenHeight/2; p2[i].x=rx; p2[i].y=ry; glVertex2d(p1[i].x,p1[i].y); glVertex2d(p2[i].x,p2[i].y); } glEnd(); for(int i=0;i<N;i+=2)//画外框 { moveTo(p1[i].x,p1[i].y); lineTo(p1[(i+2)%N].x,p1[(i+2)%N].y); } for(int i=0;i<N;i+=2)//画内角 { moveTo(p1[i].x,p1[i].y); lineTo(p2[(i+1)%N].x,p2[(i+1)%N].y); moveTo(p2[i+1].x,p2[i+1].y); lineTo(p1[(i+2)%N].x,p1[(i+2)%N].y); } //画内圆 glBegin(GL_POINTS); for(double i=0.0;i<=2*pi;i+=0.05) glVertex2d(r*cos(i)+screenWidth/2,r*sin(i)+screenHeight/2); glEnd(); glFlush(); } void myInit(void) { glClearColor(1.0,1.0,1.0,0.0); //background color glColor3f(0.0f,0.2f,0.6f); //point color glPointSize(3.0); glMatrixMode(GL_PROJECTION); glLoadIdentity(); gluOrtho2D(0.0,500,0.0,500); } int main(int argc,char ** argv) { glutInit(&argc,argv); glutInitDisplayMode(GLUT_SINGLE|GLUT_RGB); glutInitWindowPosition(0,0); glutInitWindowSize(500,500); glutCreateWindow("内外圆多边形"); glutDisplayFunc(photo); myInit(); glutMainLoop(); return 0; }
练习3.4.1
3.4.2证明
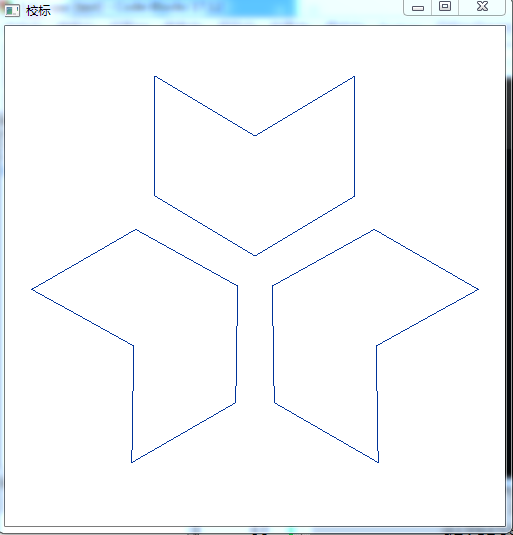
图片3.30 某大学的标志
给定一点
//3.4.3 校标 #include <windows.h> #include <gl/gl.h> #include <gl/glu.h> #include <gl/glut.h> #include <iostream> #include <math.h> using namespace std; const double screenWidth=500; const double screenHeight=500; int j=0;//声明一个全局变量 class point { public: GLdouble x; GLdouble y; void setp(GLdouble _x,GLdouble _y){x=_x;y=_y;}; }; void photo(void) { point p[6]; //定义对象数组 并且初始化 p[0].x=0; p[0].y=20; p[1].x=-100; p[1].y=80; p[2].x=-100; p[2].y=200; p[3].x=0; p[3].y=140; p[4].x=100; p[4].y=200; p[5].x=100; p[5].y=80; int N=3; double pi=3.1415926; double theta=2*pi/N; //开始画图 glClear(GL_COLOR_BUFFER_BIT); for(int j=0;j<3;j++) //j定义为全局变量 否则不能通过编译 { glBegin(GL_LINE_LOOP); for(int i=0;i<6;i++)
glVertex2d((cos(theta*j)*p[i].x-sin(theta*j)*p[i].y)+screenWidth/2,(sin(theta*j)*p[i].x+cos(theta*j)*p[i].y)+screenHeight/2); glEnd(); } glFlush(); } void myInit(void) { glClearColor(1.0,1.0,1.0,0.0); //background color glColor3f(0.0f,0.2f,0.6f); //point color glPointSize(3.0); glMatrixMode(GL_PROJECTION); glLoadIdentity(); gluOrtho2D(0.0,500,0.0,500); } int main(int argc,char ** argv) { glutInit(&argc,argv); glutInitDisplayMode(GLUT_SINGLE|GLUT_RGB); glutInitWindowPosition(0,0); glutInitWindowSize(500,500); glutCreateWindow("校标"); glutDisplayFunc(photo); myInit(); glutMainLoop(); return 0; }
3.4.3 绘制圆与圆弧
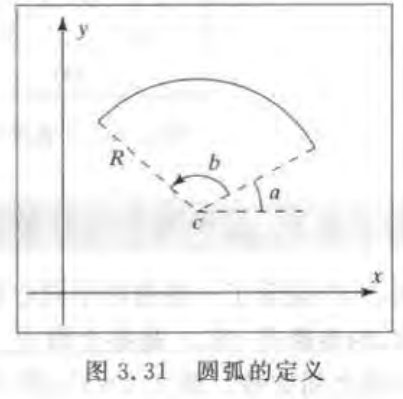
圆心:c
半径:R
开始角度:a
展开角度:b
b为负值 则顺时针画图
b为正值 则逆时针画图
展开的角度是360度
drawCirlce() 通过指定圆心和半径来绘制,还有其他的方法来描述圆,常见的方式是:
1.已知圆心以及一个院上的点。 利用圆心以及一个圆上的点 计算两点的距离即半径
2.给定圆必须经过的三个点。 三个不共线的点可以唯一确定一个圆
画圆案例2
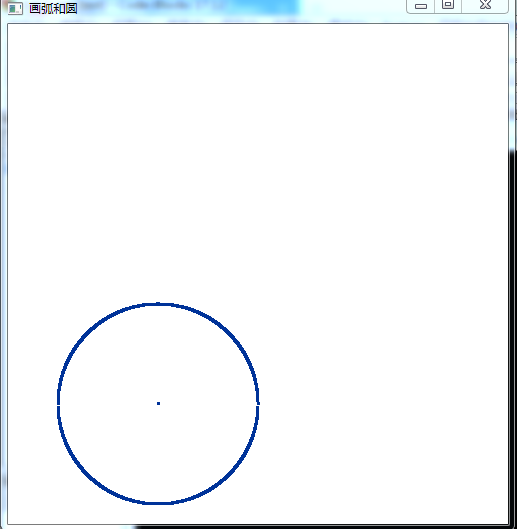
//3.4.3 圆外切 #include <windows.h> #include <gl/gl.h> #include <gl/glu.h> #include <gl/glut.h> #include <iostream> #include <math.h> using namespace std; const double screenWidth=500; const double screenHeight=500; class point { public: GLdouble x; GLdouble y; void setp(GLdouble _x,GLdouble _y){x=_x;y=_y;}; }; void photo(void) { double r=100; double x; int w=150; int h=120; glClear(GL_COLOR_BUFFER_BIT); glBegin(GL_POINTS); for(x=-100;x<100;x+=0.05) { glVertex2d(x+w,sqrt(r*r-x*x)+h); glVertex2d(x+w,-sqrt(r*r-x*x)+h); } glVertex2d(w,h); glEnd(); glFlush(); } void myInit(void) { glClearColor(1.0,1.0,1.0,0.0); //background color glColor3f(0.0f,0.2f,0.6f); //point color glPointSize(3.0); glMatrixMode(GL_PROJECTION); glLoadIdentity(); gluOrtho2D(0.0,500,0.0,500); } int main(int argc,char ** argv) { glutInit(&argc,argv); glutInitDisplayMode(GLUT_SINGLE|GLUT_RGB); glutInitWindowPosition(0,0); glutInitWindowSize(500,500); glutCreateWindow("画弧和圆"); glutDisplayFunc(photo); myInit(); glutMainLoop(); return 0; }
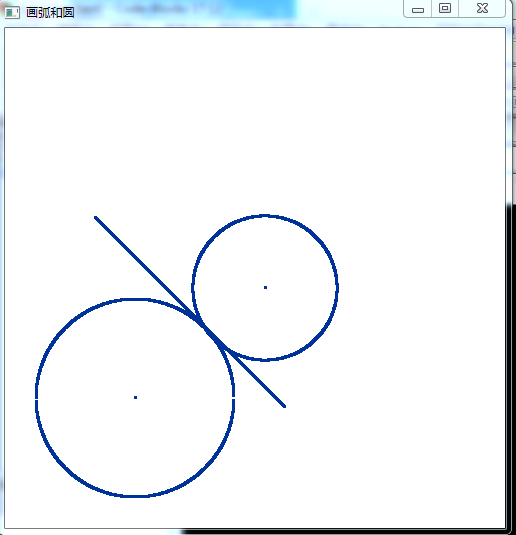
画圆案例3
//3.4.3 圆外切 给定一个两个圆心 和两个圆的交点 画两个圆和一条切线 #include <windows.h> #include <gl/gl.h> #include <gl/glu.h> #include <gl/glut.h> #include <iostream> #include <math.h> using namespace std; const double screenWidth=500; const double screenHeight=500; int w=80;//位移 int h=80; class point { public: GLdouble x; GLdouble y; void setp(GLdouble _x,GLdouble _y){x=_x;y=_y;}; }; double getr(point p1,point p2)//获取半径的平方 { double r=sqrt((p1.x-p2.x)*(p1.x-p2.x)+(p1.y-p2.y)*(p1.y-p2.y)); return r; } void line(point p1,point p2)//p1为圆心,p2为圆上点 直线过p2点 { double k,b; k=-(p2.x-p1.x)/(p2.y-p1.y); b=p2.y-k*p2.x; glBegin(GL_POINTS); for(double x=10;x<200;x++) glVertex2d(x+w,k*x+b+h); glEnd(); } void photo(point p1,point p2) //根据两个点画圆 p1为圆心 p2为圆上的点 { double r=getr(p1,p2); double x; glBegin(GL_POINTS); for(x=p1.x-r;x<=p1.x+r;x+=0.05) { glVertex2d(x+w,sqrt(r*r-(x-p1.x)*(x-p1.x))+p1.y+h); glVertex2d(x+w,-sqrt(r*r-(x-p1.x)*(x-p1.x))+p1.y+h); } glVertex2d(p1.x+w,p1.y+h); glEnd(); } void mydisplay(void) { class point p1;//初始化 三个对象 p1.x=50; p1.y=50; point p2; p2.x=120; p2.y=120; point p3; p3.x=180; p3.y=160; glClear(GL_COLOR_BUFFER_BIT); photo(p1,p2); photo(p3,p2); line(p1,p2); glFlush(); } void myInit(void) { glClearColor(1.0,1.0,1.0,0.0); //background color glColor3f(0.0f,0.2f,0.6f); //point color glPointSize(3.0); glMatrixMode(GL_PROJECTION); glLoadIdentity(); gluOrtho2D(0.0,500,0.0,500); } int main(int argc,char ** argv) { glutInit(&argc,argv); glutInitDisplayMode(GLUT_SINGLE|GLUT_RGB); glutInitWindowPosition(0,0); glutInitWindowSize(500,500); glutCreateWindow("画弧和圆"); glutDisplayFunc(mydisplay); myInit(); glutMainLoop(); return 0; }
执行结果:
3.4.4曲线的逐次细化
逐次细化一个简单的曲线,可以递归形成非常复杂的曲线。 例如koch曲线 逐渐逼近真实的曲线
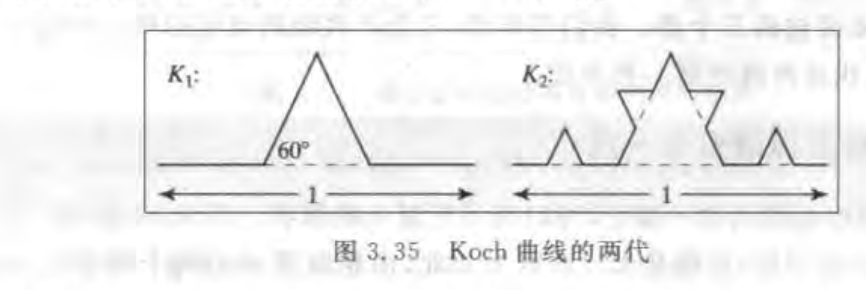
将kn的每一条线段平均分为3的段,然后将中间的那段用一个等边三角形来提高代替,采用递归的方式,每一线段的长度变为原来的4/3,所以总的曲线长度也是它上一代的4/3.因此kn的总长度为(4/3)的n次幂。
3.5曲线的参数形式
描述曲线的形状主要有两种方法:
隐式法和参数形式
隐式法:使用函数f(x,y)来描述曲线 并且提供xy之间的关系
点在曲线上的条件:f(x,y)=0
一类曲线 曲线的内部和外部是有意义的,此种情况下 f(x,y)也被叫做内部-外部函数 其意义是:
f(x,y)=0 对应所有在曲线上的点 (x,y)
f(x,y)>0 对所有在曲线外的点(x,y)
f(x,y)<0 对所有在曲线内的点(x,y)
曲线对x是单值 那么 g(x)对于每一个x 仅有一个g(x) 可以写成f(x,y)=y-g(x)
曲线对y是单值, 存在函数h() 使得曲线上的所有点满足x=h(y)
还有对于x和y都不是单值的:f(x,y)=0 不能写成y=g(x) 或者 x=h(y)的形式 可以表示成:
y=+-根号下(r^2-x^2) 这里为两个函数 一个是正号,另一个是负号
3.5.1曲线的参数形式
当参数取不同值的时候,会产生出曲线上不同的点。推荐使用 以时间t的运动轨迹
粒子沿着曲线运动的路径由两个函数x()和y()来确定,如果是三维 则有三个函数 x() y() z() 他们确定粒子在时刻t的位置。
参数t通常被看作是时间,而曲线本身就是粒子随着时间在某一个区间内的变化所经过的点。
通常证明隐式形式和参数形式相同 将参数形式带入隐式形式即可 即从参数形式求隐式形式
3.5.2 绘制参数形式
根据p(t)=(x(t),y(t)) 其中t从0变化到T 我们只需要用非常紧凑的间隔采集p(t)的样本 然后连接成折线 近似的逼近曲线
时间数组 t[i] i=0 1 2 3...
glBegin(GL_LINES); for(int i=0;i<n;i++) glVertex2f(x(t[i]),y(t[i])); glEnd();
案例绘制椭圆
glBegin(GL_LINES); for(double t=0;t<2*pi;t+=2*pi/n)//将2pi n等分 越细分曲线越光滑 glVertex2f(W*cos(t),H*sin(t)); glEnd();
3.5.4 样例曲线代码
//3.4.3 圆外切 给定一个两个圆心 和两个圆的交点 画两个圆和一条切线 #include <windows.h> #include <gl/gl.h> #include <gl/glu.h> #include <gl/glut.h> #include <iostream> #include <math.h> using namespace std; const double screenWidth=500; const double screenHeight=500; int w=180;//位移 int h=80; const double pi=3.141592; const int n=360; void mydisplay(void) { glClear(GL_COLOR_BUFFER_BIT); glBegin(GL_LINE_LOOP); for(double t=0.0;t<2*pi;t+=2*pi/n) glVertex2d(w*cos(t)+screenWidth/2,h*sin(t)+screenHeight/2); glEnd(); glFlush(); } void myInit(void) { glClearColor(1.0,1.0,1.0,0.0); //background color glColor3f(0.0f,0.2f,0.6f); //point color glPointSize(3.0); glMatrixMode(GL_PROJECTION); glLoadIdentity(); gluOrtho2D(0.0,500,0.0,500); } int main(int argc,char ** argv) { glutInit(&argc,argv); glutInitDisplayMode(GLUT_SINGLE|GLUT_RGB); glutInitWindowPosition(0,0); glutInitWindowSize(500,500); glutCreateWindow("画椭圆"); glutDisplayFunc(mydisplay); myInit(); glutMainLoop(); return 0; }
执行结果

3.5.5 画图
//3.4.3 圆外切 给定一个两个圆心 和两个圆的交点 画两个圆和一条切线 #include <windows.h> #include <gl/gl.h> #include <gl/glu.h> #include <gl/glut.h> #include <iostream> #include <math.h> using namespace std; const double screenWidth=500; const double screenHeight=500; int w=180;//位移 int h=140; const float f=h/w; double d=0.5; double t=d*f; const double pi=3.141592; const int n=360; const float color1[3]={1.0,1.0,1.0}; const float color2[3]={0.0,0.0,0.0}; void drawEllipse(int w,int h,const float * clr)//画圆并填充 { if(w!=h) { glBegin(GL_POINTS); for(;w>0&&h>0;w-=d,h-=t) { glColor3f(clr[0],clr[1],clr[2]); for(double t=0.0;t<2*pi;t+=2*pi/n) glVertex2d(w*cos(t)+screenWidth/2,h*sin(t)+screenHeight/2); } glEnd(); } if(w==h) { glBegin(GL_POINTS); for(;w>0&&h>0;w-=d) { glColor3f(clr[0],clr[1],clr[2]); for(double t=0.0;t<2*pi;t+=2*pi/n) glVertex2d(w*cos(t)+screenWidth/2,w*sin(t)+screenHeight/2); } glEnd(); } } void mydisplay(void) { glClear(GL_COLOR_BUFFER_BIT); drawEllipse(w,h,color2); drawEllipse(h-5,h-5,color1); drawEllipse(h-10,h-50,color2); drawEllipse(h-55,h-55,color1); glFlush(); } void myInit(void) { glClearColor(1.0,1.0,1.0,0.0); //background color glPointSize(3.0); glMatrixMode(GL_PROJECTION); glLoadIdentity(); gluOrtho2D(0.0,500,0.0,500); } int main(int argc,char ** argv) { glutInit(&argc,argv); glutInitDisplayMode(GLUT_SINGLE|GLUT_RGB); glutInitWindowPosition(0,0); glutInitWindowSize(500,500); glutCreateWindow("画椭圆"); myInit(); glutDisplayFunc(mydisplay); glutMainLoop(); return 0; }
执行结果

3.5.3极坐标形式

用来表示和绘制一些有趣曲线
极坐标画圆
//3.4.3 圆外切 给定一个两个圆心 和两个圆的交点 画两个圆和一条切线 #include <windows.h> #include <gl/gl.h> #include <gl/glu.h> #include <gl/glut.h> #include <iostream> #include <math.h> using namespace std; const double screenWidth=500; const double screenHeight=500; double pi=3.1415926; void drawEllipse(double k)//极坐标画圆 { double theta=0; glBegin(GL_POINTS); for(;theta<=2*pi;theta+=0.01) { glVertex2d(k*cos(theta)+screenWidth/2,k*sin(theta)+screenHeight/2); } glEnd(); } void mydisplay(void) { glClear(GL_COLOR_BUFFER_BIT); drawEllipse(200); glFlush(); } void myInit(void) { glClearColor(1.0,1.0,1.0,0.0); //background color glPointSize(3.0); glColor3f(1.0,0.0,0.0); glMatrixMode(GL_PROJECTION); glLoadIdentity(); gluOrtho2D(0.0,500,0.0,500); } int main(int argc,char ** argv) { glutInit(&argc,argv); glutInitDisplayMode(GLUT_SINGLE|GLUT_RGB); glutInitWindowPosition(0,0); glutInitWindowSize(500,500); glutCreateWindow("极坐标画圆"); glutDisplayFunc(mydisplay); myInit(); glutMainLoop(); return 0; }
执行结果
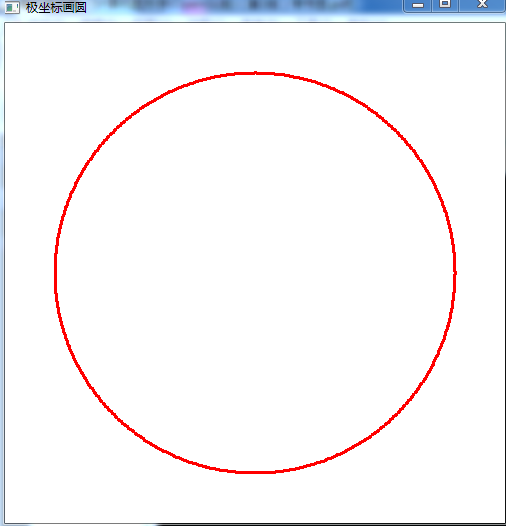
极坐标画心形
替换上面的函数代码段
void drawEllipse(double k)//极坐标画圆 { double theta=0; glBegin(GL_POINTS); for(;theta<=2*pi;theta+=0.01) { double f=k*(1+cos(theta)); glVertex2d(f*cos(theta)+screenWidth/3,f*sin(theta)+screenHeight/2); } glEnd(); }
执行结果

玫瑰曲线 图3.45
代码段替换
void drawEllipse(double k,int n)//极坐标画圆 n为花瓣 { double theta=0; glBegin(GL_LINES); for(;theta<=2*pi;theta+=0.00001) { double f=k*cos(n*theta); glVertex2d(f*cos(theta)+screenWidth/2,f*sin(theta)+screenHeight/2); glVertex2d(f*cos(theta+0.00001)+screenWidth/2,f*sin(theta+0.01)+screenHeight/2); } glEnd(); } void mydisplay(void) { glClear(GL_COLOR_BUFFER_BIT); drawEllipse(200,8); glFlush(); }
执行结果

阿基米德螺旋线
替换代码段
void drawEllipse(double k,int n)//极坐标画圆 n为圈数 { double theta=0; glBegin(GL_POINTS); for(;theta<=n*pi;theta+=0.01) { double f=k*theta; glVertex2d(f*cos(theta)+screenWidth/2,f*sin(theta)+screenHeight/2); } glEnd(); }

以上各类函数如下:


圆锥曲线代码
void drawEllipse(double e)//极坐标画圆 n为圈数 { double theta=0; glBegin(GL_POINTS); for(;theta<=2*pi;theta+=0.0001) { double f1=1/(1-e*cos(theta)); //double f2=1/(1+e*cos(theta)); glVertex2d(f1*cos(theta)+screenWidth/4,f1*sin(theta)+screenHeight/2); //glVertex2d(f2*cos(theta)+screenWidth/2,f2*sin(theta)+screenHeight/2); } glEnd(); }
对数螺旋线
void drawEllipse(double e)//极坐标画圆 n为圈数 调用时 e的值需要大于1 { double theta=0; double k=0.8; double a=0.6; glBegin(GL_POINTS); for(;theta<=16*pi;theta+=0.01) { double f1=k*pow(e,a*theta);//e的a*theta次幂 //double f2=1/(1+e*cos(theta)); glVertex2d(f1*cos(theta)+screenWidth/2,f1*sin(theta)+screenHeight/2); //glVertex2d(f2*cos(theta)+screenWidth/2,f2*sin(theta)+screenHeight/2); } glEnd(); }

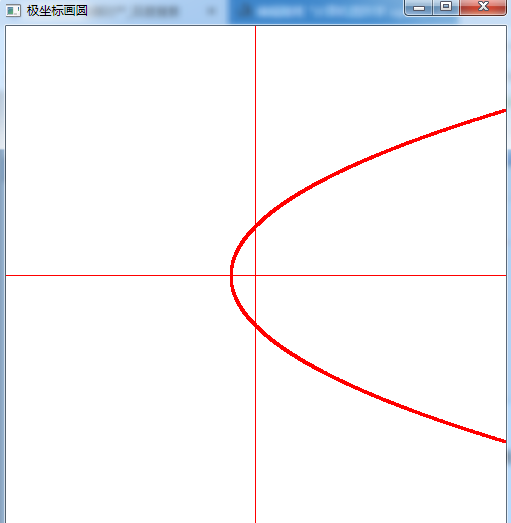
双曲线
void drawEllipse(double e,double p)//极坐标画圆 n为圈数 e大于1 { double theta=0; glBegin(GL_POINTS); for(;theta<=2*pi;theta+=0.001) { double f1=e*p/(1-e*cos(theta));//圆锥曲线通用方程 p为焦点到准线的距离 f1表示数学中极坐标的径向距离 glVertex2d(f1*cos(theta)+screenWidth/2,f1*sin(theta)+screenHeight/2); } glEnd(); glBegin(GL_LINES); //x轴 glVertex2d(0,250); glVertex2d(500,250); glEnd(); glBegin(GL_LINES); //y轴 glVertex2d(250,0); glVertex2d(250,500); glEnd(); }

由上例可知 双曲线的右焦点为极坐标系的极点 用到的公式如下

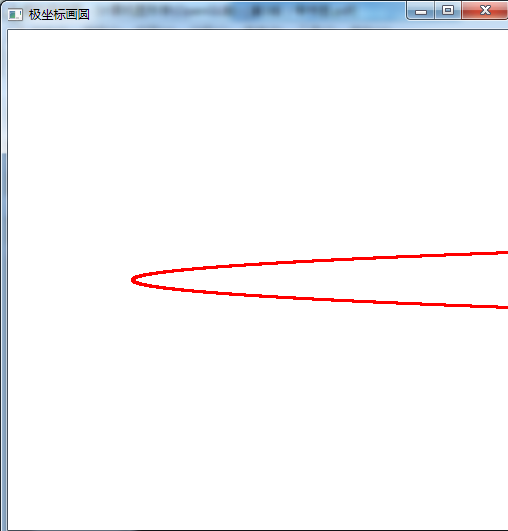
同理可得椭圆的极坐标画图代码及图像
void drawEllipse(double e,double p)//极坐标画圆 n为圈数 e小于1 { double theta=0; glBegin(GL_POINTS); for(;theta<=2*pi;theta+=0.001) { double f1=e*p/(1-e*cos(theta));//圆锥曲线通用方程 p为焦点到准线的距离 f1表示数学中极坐标的径向距离 glVertex2d(f1*cos(theta)+screenWidth/2,f1*sin(theta)+screenHeight/2); } glEnd(); glBegin(GL_LINES); //x轴 glVertex2d(0,250); glVertex2d(500,250); glEnd(); glBegin(GL_LINES); //y轴 glVertex2d(250,0); glVertex2d(250,500); glEnd(); }
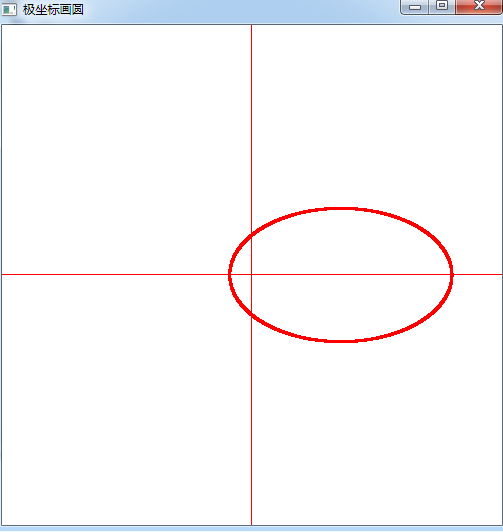
可以看出 椭圆的左焦点为 极坐标的极点
同理上面代码中e=1时 是抛物线 开口向右 极点为焦点