数据可视化(Data Visualization)
借助于图形化手段,清晰有效地传达与沟通信息。
一维数据比较简单,可以做成饼图、直方图、曲线等等…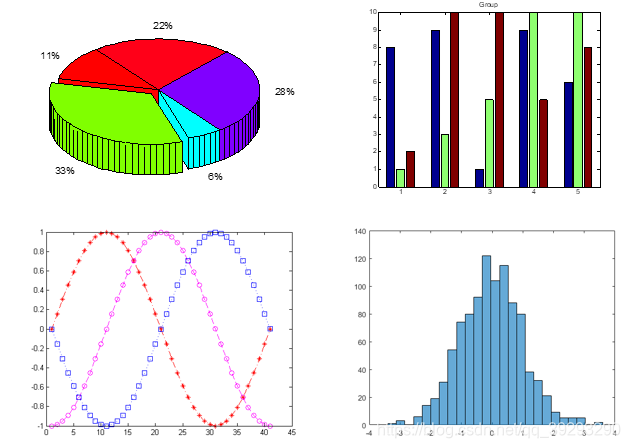
二维数据的可视化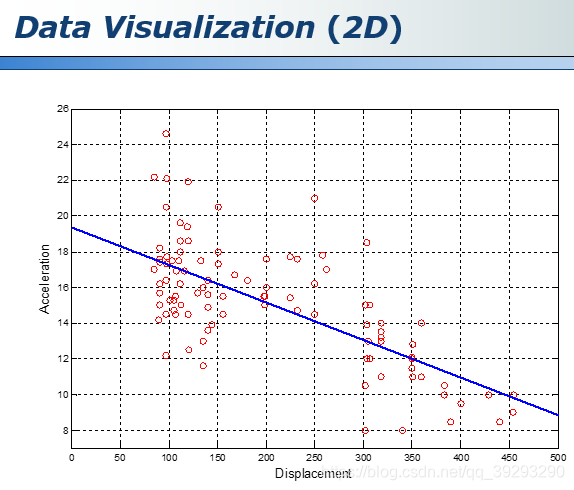
散点图,上图是汽车排量和加速度之间的关系图,我们可以对该二位数据做回归 Regression 看看它们之间有什么关系。
三维数据的可视化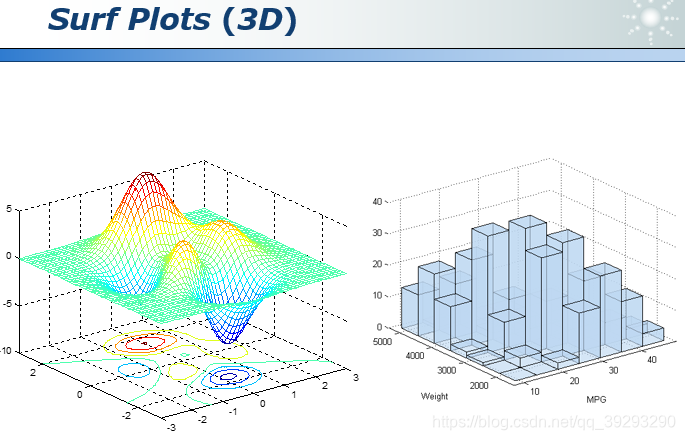
但是当维度到四维或者更高的维度时,一般人很难想象这些高维的空间,也很难直接可视化出来,这时我们可以将高维数据做一个映射和转化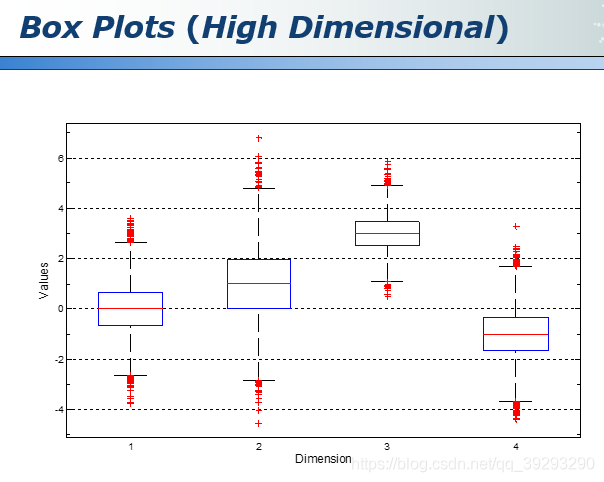
Box plots 是 matlab 中的一个函数,将这些维度依次排开在横坐标上依次展示,但是这种方法丧失了各个维度之间的关联,因为每一个维度是单独显示的。
还有一种方法是 Paraller Coordinates,这是一种比较直观将高维数据可视化的方法。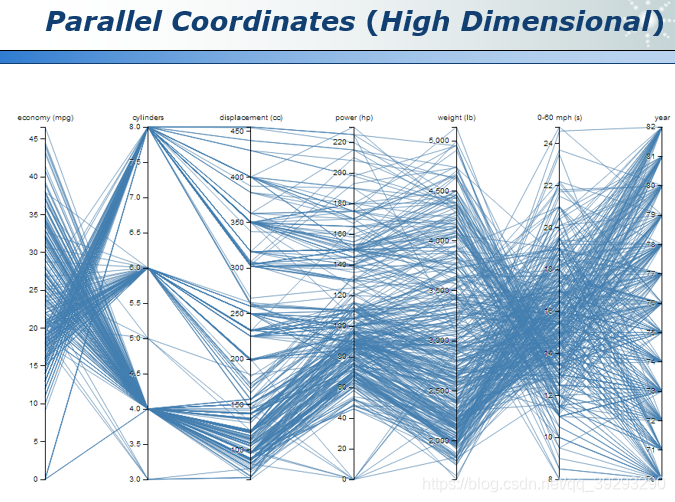
Paraller Coordinates主要是分成 2 个部分, 一个是parallel axe (平行的坐标轴), 一个是polyline(多段线). parallel axe 表示数据集(data set)的一个属性或者说变量(attribute), 每一根折线都代表一个样本。
特征选择(Feature Selection)
当我们做特定分析的时候,可能属性非常多,但有些属性是不相关的,有些属性是重复的,所以我们需要用Feature Selection挑选出来最相关的属性降低问题难度。
熵增益(Entropy Information Gain)
此处引入熵(Entropy)的概率来衡量系统的不确定性,下图第一行是计算熵的公式,如果不知道是否抽烟的信息,则熵值为1,即不确定性最高。然后分别计算出不抽烟人群的熵值为0.7219,抽烟人群的熵值为0.2864,整体熵值为0.5477, 1-0.5477=0.4523, 这个数字就是信息增量(Information Gain)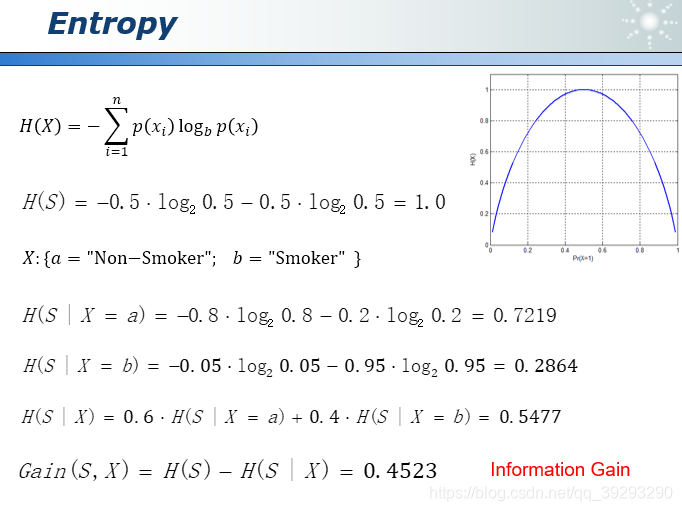
Branch and Bound(分支定界)
如果我们想从n个属性中挑选出m个最优属性,需要注意算法复杂度会随n的增长呈现指数级爆炸增长,计算量会变得非常大,为了降低复杂度这里引入了分支定界的剪枝算法。比如我们要从5个属性中挑选出两个相关性最强的属性,可以先画一个top-down的搜索树,每当往下推一层就减少一个属性,根据属性的单调性假设,属性越少效能越低,所以如果发现节点(1,3,4,5)小于左边某个只有两个属性的节点(2,3)的效能,则可以忽略节点(1,3,4,5)下面的计算,把这一整支都直接删除,从而减少计算量。
特征选择还有sequential forward, sequential backward, simulated annealing(模拟退火), tabu search(竞技搜索), genetic algorithms(遗传算法)等方式去优化。
主成分分析PCA
PCA主要目的是降维,分析主成分提取最大的个体差异变量,削减回归分析和聚类分析中变量的数目,方式是通过正交变换将一系列可能线性相关的变量转换为一组线性不相关的新变量。
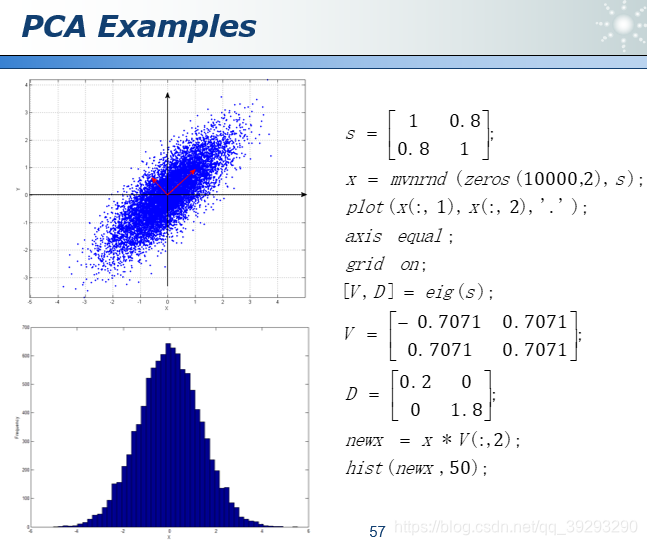
先看一个二维图像的例子,左边是原始数据,横轴和纵轴可以当作高和宽,经过转换,实际是把坐标顺时针转动了60度,这样一来纵轴的差异就很小了, 这需要一点线性代数知识来生成转置矩阵。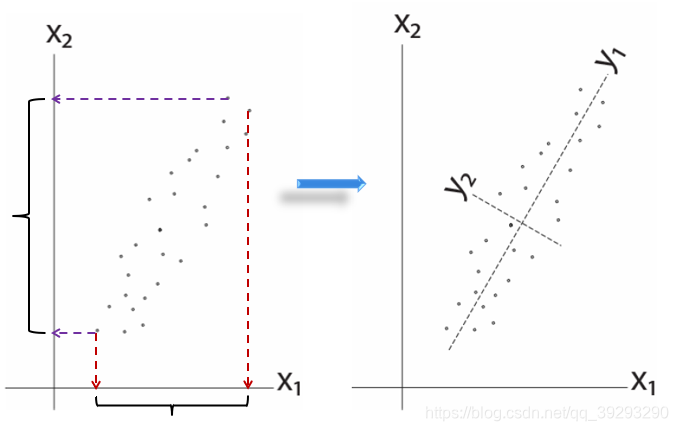
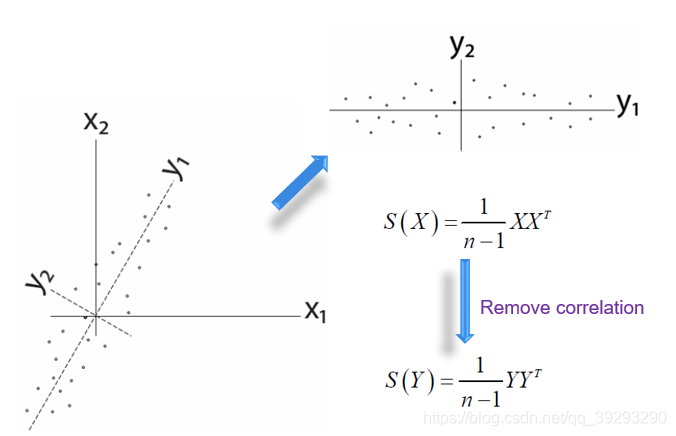
我们希望Y是一个对角阵,如果要让坐标变化就要让原矩阵X乘以一个旋转矩阵P, n只是一个scale可以忽略。要确保Y是一个对角阵,那么P和Q必须互逆,即Q就是P的转置矩阵。
从另外一个角度再看,我们希望原点和映射点的距离的平方和最小,即目标函数 J ( e ) 最小,经过几步推到可以看到要让 J ( e )最小其实也就是要让右下角的 S 最大。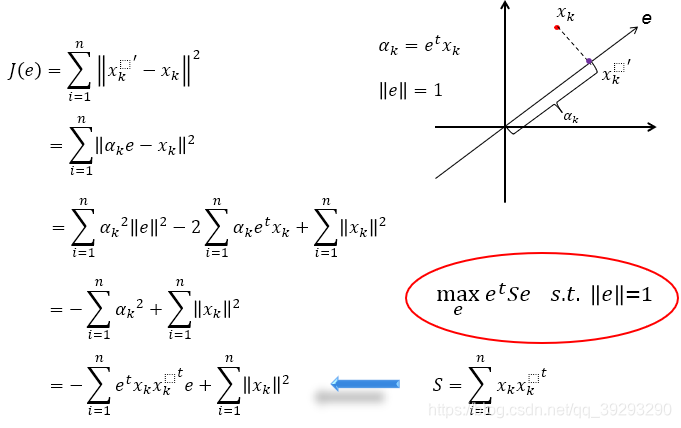
这就成了一个带条件的约束问题,可以用拉格朗日乘数法来求解。我们就是要将 λ最大化,而 λ 也就是特征值。
不管多少维空间,我们可以用一根投影轴线插进去,让空间中的每个点与这个线上某个点的距离的平方和最小,线上的这个点就是高维空间的投影了。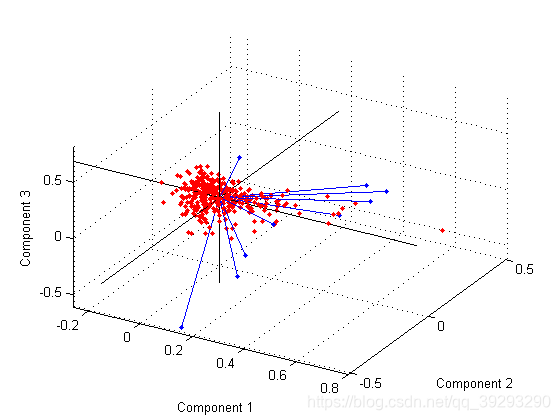
线性判别分析(Linear Discriminant Analysis)
LDA的原理是,将带上标签的数据(点),通过投影的方法,投影到维度更低的空间中,使得投影后的点,会形成按类别区分,一簇一簇的情况,相同类别的点,将会在投影后的空间中更接近。虽然也是降维,但好的LDA算法对不同类别是有明显的区分度的。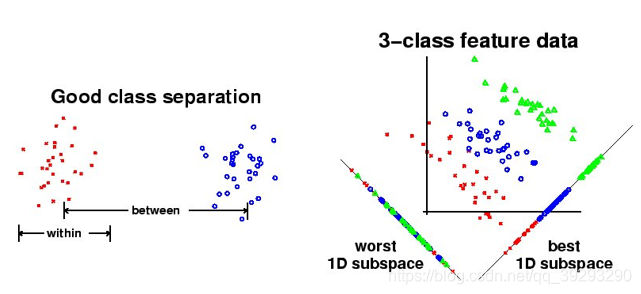
LDA的目标函数如下: 分类的目标是,使得类别内的点距离越近越好(集中),类别间的点越远越好。分母表示每一个类别内的方差之和,方差越大表示一个类别内的点越分散,分子为两个类别各自的中心点的距离的平方,我们最大化 J 就可以求出最优的 w 了, 求解同样会用到拉格朗日乘数法