极坐标与直角坐标的相互转化

前言

在平面直角坐标系 \(xOy\) 中，以原点 \(O\) 为极点，以 \(x\) 轴非负半轴为极轴建立极坐标系，如下图所示。

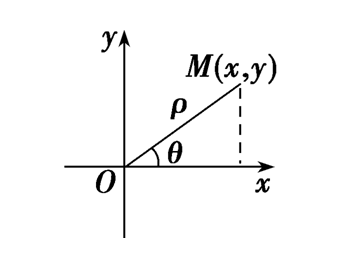
则同样的几何对象[点，线，面，等等]，比如点 \(M\)，它会既有平面直角坐标 \((x,y)\)，也会有极坐标 \((\rho,\theta)\)，那么这二者之间必然会有相互转化的桥梁。

相互转化

• 极坐标化为直角坐标，指的是将包含 \(\rho\) 和 \(\theta\) 的方程 \(f(\rho,\theta)=0\) 等价转化为不含有 \(\rho\) 和 \(\theta\) ，而只含有 \(x\) 和 \(y\) 的方程 \(g(x,y)=0\)，经常使用的变形有给等式的两边同时乘以 \(\rho\)[或除以 \(\rho\) ] ，或同时平方；

使用公式：\(\rho^2=x^2+y^2\)，\(\rho\cdot \cos\theta=x\)，\(\rho\cdot \sin\theta=y\)，\(\tan\theta=\cfrac{y}{x}\)；

举例：①\(\rho=2\cos\theta\)，两边同乘以\(\rho\)，得到\(\rho^2=2\rho\cos\theta\)，即 \(x^2+y^2=2x\)由极坐标方程化为直角坐标方程时要注意变形的等价性，通常总要用 \(\rho\) 去乘方程的两端，应该检查极点是否在曲线上，若在，是等价变形，否则，不是等价变形。；

②\(\rho=\cfrac{\sqrt{10}}{\sqrt{1+9\sin^2\theta}}\)，两边同时平方并整理，得到\(\rho^2(1+9\sin^2\theta)=10\)，

即\(\rho^2+9(\rho\sin\theta)^2=10\)，即\(x^2+10y^2=10\)

③ \(\rho=\cfrac{6}{1-2\cos\theta}\) ，

化简方法，去分母，移项[应该移动哪一项]，平方的顺序，

• 直角坐标化为极坐标，指的是将包含 \(x\) 和 \(y\) 的方程 \(m(x,y)=0\) 等价转化为不含有 \(x\) 和 \(y\) ，而只含有 \(\rho\) 和 \(\theta\) 的方程 \(n(\rho,\theta)=0\)，经常使用的变形有给等式的两边同时除以 \(\rho\)；

使用公式：\(x^2+y^2=\rho^2\)，\(x=\rho\cdot\cos\theta\)，\(y=\rho\cdot\sin\theta\)；

举例：③由\(x^2+y^2=2x\)得到，即\(\rho^2=2\rho\cos\theta\)，即\(\rho(\rho-2\cos\theta)=0\)，

故得到\(\rho=0\)，或\(\rho=2\cos\theta\)，而\(\rho=2\cos\theta\)中包含\(\rho=0\)，

故得到结果为\(\rho=2\cos\theta\)，相当于上述变形中直接约去\(\rho\) ；

典例剖析

已知点 \(P\) 的直角坐标按伸缩变换 \(\left\{\begin{array}{l}x'=2x,\\ y'=\sqrt{3}y\end{array}\right.\) 变换为点 \(P(6,-3)\)， 限定 \(\rho>0\)，\(0\)\(\leqslant\)\(\theta\)\(<\)\(2\pi\) 时， 求点 \(P\) 的极坐标。

解 设点 \(P\) 的直角坐标为 \((x, y)\)，由题意得 \(\left\{\begin{array}{l}6=2x,\\-3=\sqrt{3}y,\end{array}\right.\) 解得 \(\left\{\begin{array}{l}x=3,\\y=-\sqrt{3},\end{array}\right.\)

所以 点 \(P\) 的直角坐标为 \((3,-\sqrt{3})\)，

\(\rho=\sqrt{3^{2}+(-\sqrt{3})^{2}}=2\sqrt{3}\)， \(\tan \theta=\cfrac{-\sqrt{3}}{3}\)，

\(0 \leqslant \theta<2 \pi\)， 点 \(P\) 在第四象限， \(\theta=\cfrac{11 \pi}{6}\)，

故点 \(P\) 的极坐标为 \(\left(2\sqrt{3}, \cfrac{11\pi}{6}\right)\) .