前言
初中知识储备:同弧所对的圆周角相等。
案例分析
解析:根据正弦定理可得 \((2+b)(a-b)=(c-b)c\),
因为 \(a=2\), 代入得 \(a^{2}-b^{2}=c^{2}-bc\), 即 \(b^{2}+c^{2}-a^{2}=bc\),
根据余弦定理得 \(\cos A=\cfrac{b^{2}+c^{2}-a^{2}}{2bc}=\cfrac{1}{2}\),
因为 \(0<A<\pi\), 所以 \(A=\cfrac{\pi}{3}\),这样便得到该三角形一条边 \(a\) 及其对角 \(A\) 的条件.
画出该三角形, 如图,可以发现这是一个顶角为 \(\cfrac{\pi}{3}\), 底边长为 \(2\) 的三角形,
由正弦定理 \(\cfrac{a}{\sin A}=\cfrac{2}{\sin\cfrac{\pi}{3}}=\cfrac{4 \sqrt{3}}{3}=2R\),
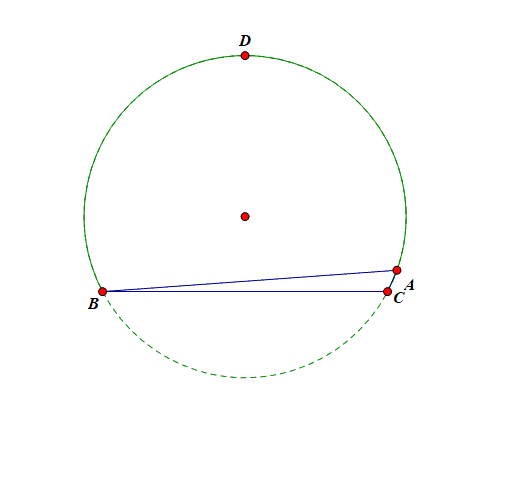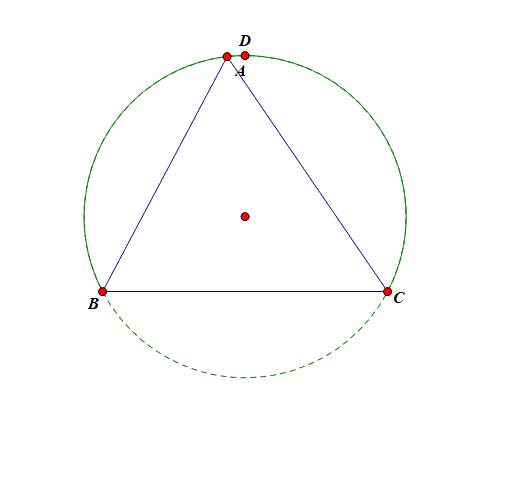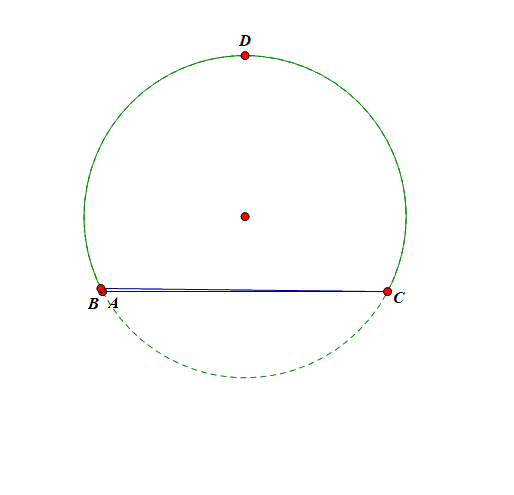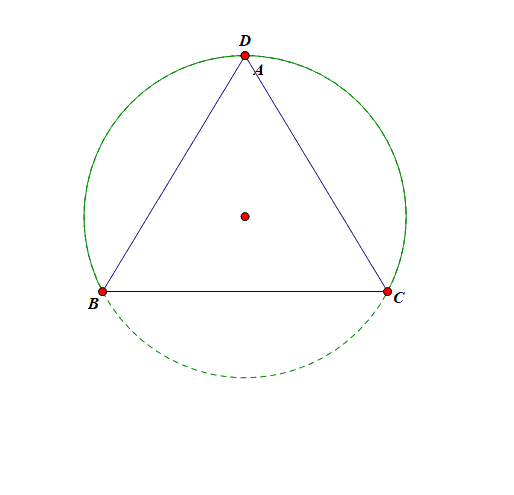
从运动变化的角度来看, 顶点 \(A\) 在半径为 \(R=\cfrac{2 \sqrt{3}}{3}\) 的圆上运动, 当且仅当点 \(A\) 运动到 \(BC\) 的中垂线与 \(\odot O\) 的优弧的交点 \(D\) 处, \(\triangle ABC\) 的面积取得最大值 \(\sqrt{3}\), 此时 \(\triangle ABC\) 为等边三角形,故 \(\triangle ABC\) 面积的最大值为 \(\sqrt{3}\) .
〔解后反思〕:1、本题从条件来看, 给出了一个角 \(A=\cfrac{\pi}{3}\) 及其对边 \(a=2\), 这其实就是确定了顶点 \(A\) 的运动范围,其必须在优弧 \(\overset{\frown}{BC}\)上运动,不能在劣弧 \(\overset{\frown}{BC}\) 上运动,否则角 \(A=\cfrac{2\pi}{3}\) 。 相对来说, 面积 \(S=\cfrac{1}{2}\cdot a\cdot h\) 中的底长度是确定的,高 \(h\) 是待定的,则高越大,面积就越大。从运动变化的角度更容易把握问题本质。在这个背景下的面积最值一般结果为 \(S_{\max }\)\(=\)\(\cfrac{1}{2}\cdot a\cdot\cfrac{a}{2\tan\frac{A}{2}}\)\(=\)\(\cfrac{a^{2}}{4\tan\frac{A}{2}}\).
2、使用本方法,从形的角度思考,能求解面积的取值范围吗?回答是肯定的,当顶点 \(A\) 到达点 \(D\) 时,面积达到最大,根据图形的对称性,我们很容易理解,当顶点 \(A\) 从点 \(D\) 往点 \(B\) 或点 \(C\) 运动时,面积必然会逐渐减小,到达点 \(B\) 或点 \(C\) 时,面积为\(0\),故面积的取值范围为 \(\left(0,\sqrt{3}\;\right]\);
从数的角度验证如下:
由于题目已知\(A=\cfrac{\pi}{3},a=2\),则\(B+C=\cfrac{2\pi}{3}\),故\(B,C\in (0,\cfrac{2\pi}{3})\),且\(C=\cfrac{2\pi}{3}-B\),
则由正弦定理得\(\cfrac{b}{sinB}=\cfrac{c}{sinC} =\cfrac{a}{sinA} =\cfrac{2}{\frac{\sqrt{3}}{2}} =\cfrac{4\sqrt{3}}{3}\),
则\(b=\cfrac{4\sqrt{3}}{3}sinB\),\(c=\cfrac{4\sqrt{3}}{3}sinC\),
则\(bc=(\cfrac{4\sqrt{3}}{3})^2\cdot sinB\cdot sinC=\cfrac{16}{3}sinB\cdot sin(\cfrac{2\pi}{3}-B)\) [1]
\(=\cfrac{16}{3}sinB\cdot (\cfrac{\sqrt{3}}{2}cosB+\cfrac{1}{2}sinB)\) \(=\cdots\)
\(=\cfrac{8}{3}sin(2B-\cfrac{\pi}{6})+\cfrac{4}{3}\)
由于 \(B\in (0,\cfrac{2\pi}{3})\) ,故\(-\cfrac{\pi}{6}<2B-\cfrac{\pi}{6}<\cfrac{7\pi}{6}\),
即\(-\cfrac{1}{2}<sin(2B-\cfrac{\pi}{6})\leqslant1\),即\(0<bc\leqslant 4\),
又由于\(S_{\triangle}=\cfrac{1}{2}bc\cdot sinA=\cfrac{\sqrt{3}}{4}\cdot bc\),
则 \(0<\cfrac{1}{2}bc\cdot sinA\leqslant \sqrt{3}\),即 \(0<S_{\triangle}\leqslant \sqrt{3}\) .
〔原创改编〕:已知 \(a\), \(b\), \(c\) 分别为 \(\triangle ABC\) 的内角 \(A\), \(B\), \(C\) 的对边, \(a=2\), 且 \(A=\cfrac{\pi}{3}\), 我们既可以使用正弦型求解 \(\triangle ABC\) 的取值范围,也可以采用动态运动的观点求解 \(\triangle ABC\) 的取值范围,你能求解 \(\triangle ABC\) 面积的取值范围吗 ________.
探究应用
(1).求角\(A\).
分析:由已知\(\vec{m}//\vec{n}\),可得到\(a\cos C+\sqrt{3}a\sin C-b-c=0\),
由正弦定理边化角可得,\(\sin A\cos C+\sqrt{3}\sin A\sin C-\sin B-\sin C=0\),
由于\(B=\pi-A-C\),则有\(\sin A\cos C+\sqrt{3}\sin A\sin C-\sin(A+C)-\sin C=0\),
整理得到,\(\sqrt{3}\sin A\sin C-\cos A\sin C-\sin C=0\),
由于\(\sin C\neq 0\),则得到\(\sqrt{3}\sin A-\cos A-1=0\),
由辅助角公式可得,\(2\sin(A-\cfrac{\pi}{6})=1\),
即\(\sin(A-\cfrac{\pi}{6})=\cfrac{1}{2}\),
由\(0<A<\cfrac{\pi}{2}\),则\(-\cfrac{\pi}{6}<A-\cfrac{\pi}{6}<\cfrac{\pi}{3}\),
则\(A-\cfrac{\pi}{6}=\cfrac{\pi}{6}\),故\(A=\cfrac{\pi}{3}\).
(2).若\(a=3\),求\(\triangle ABC\)面积的取值范围。
法1:使用均值不等式求解;此时已知 \(A=\cfrac{\pi}{3}\),\(a=3\),
由余弦定理可知,\(a^2=b^2+c^2-2bc\cos A\),即\(3^2=b^2+c^2-bc=(b+c)^2-3bc\);
即 \((b+c)^2=9+3bc\geqslant (2\sqrt{bc})^2=4bc\),即 \(bc\leqslant 9\) ;
即\(S_{\triangle ABC}=\cfrac{1}{2}bc\cdot\sin A=\cfrac{\sqrt{3}}{4}bc\),
故 \(\cfrac{\sqrt{3}}{4}bc\leqslant \cfrac{9\sqrt{3}}{4}\); 故 \([S_{\triangle ABC}]_{\max}=\cfrac{9\sqrt{3}}{4}\);
本解法的缺陷:不能求解面积的最小值。
法2: 由\(\cfrac{b}{\sin B}=\cfrac{c}{\sin C}=\cfrac{a}{\sin A}=\cfrac{3}{\frac{\sqrt{3}}{2}}=2\sqrt{3}\),
则得\(b=2\sqrt{3}\sin B\), \(c=2\sqrt{3}\sin C\),\(C=\cfrac{2\pi}{3}-B\),
所以\(bc=12\sin B\sin C=12\sin B\sin(\cfrac{2\pi}{3}-B)=12\sin B\sin(\cfrac{\pi}{3}+B)\)
\(=12\sin B(\cfrac{\sqrt{3}}{2}\cdot \cos B+\cfrac{1}{2}\cdot\sin B)=6\sqrt{3}\sin B\cos B+6\sin^2B\)
\(=3\sqrt{3}\sin2B+3(1-\cos2B)=3\sqrt{3}\sin2B-3\cos2B+3\)
\(=6(\cfrac{\sqrt{3}}{2}\sin2B-\cfrac{1}{2}\cos2B)+3=6\sin(2B-\cfrac{\pi}{6})+3\)
由于\(\triangle ABC\)为锐角三角形,所以\(\left\{\begin{array}{l}0<B<\cfrac{\pi}{2}\\ 0<\cfrac{2 \pi}{3}-B<\cfrac{\pi}{2}\end{array}\right.\), 解得\(\cfrac{\pi}{6}<B<\cfrac{\pi}{2}\)
所以\(\cfrac{\pi}{6}<2B-\cfrac{\pi}{6}<\cfrac{5\pi}{6}\),\(\cfrac{1}{2}<\sin(2B-\cfrac{\pi}{6})\leqslant 1\),
故\(6<6\sin(2B-\cfrac{\pi}{6})+3\leqslant 9\),即\(6<bc\leqslant9\)
又由于\(S_{\triangle_{ABC}}=\cfrac{1}{2}bc\sin A=\cfrac{\sqrt{3}}{4}bc\)
故\(\cfrac{3\sqrt{3}}{2}<\cfrac{\sqrt{3}}{4}bc\leqslant \cfrac{9\sqrt{3}}{4}\)
所以, \(\triangle ABC\) 面积的取值范围为\((\cfrac{3\sqrt{3}}{2}, \cfrac{9\sqrt{3}}{4}]\).
法3:使用动态的观点求解;
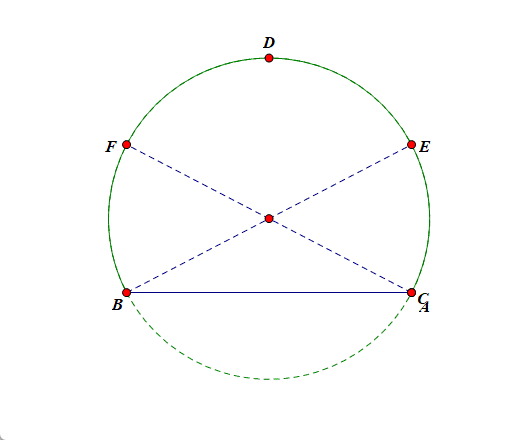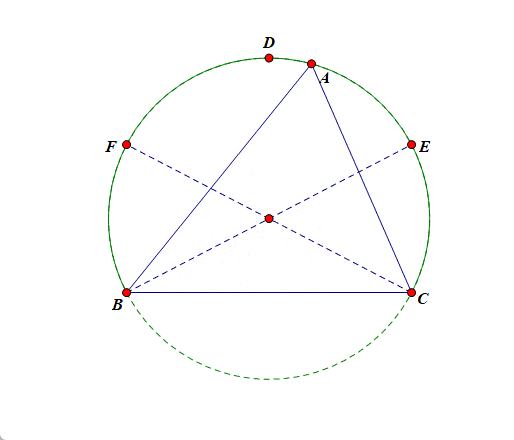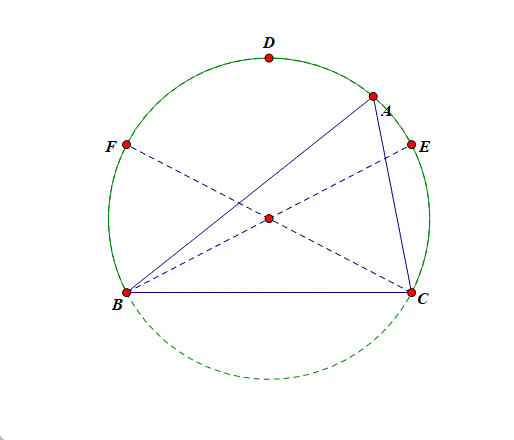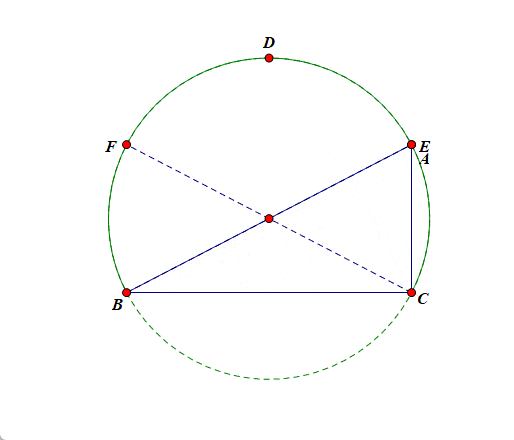
如图所示,做出锐角\(\triangle ABC\),则顶点 \(A\) 首先应该在优弧 \(\overset{\frown}{BC}\)上运动,不能在劣弧 \(\overset{\frown}{BC}\) 上运动,为了保证三角形为锐角三角形,我们还必须添加其他限制条件,简单点想,首先考虑其中的一个临界位置,比如考虑面积的最大值,则顶点 \(A\) 应该在点 \(D\) 处,此时三角形为等边三角形,\(S_{\max}\)\(=\)\(\cfrac{\sqrt{3}}{4}\times3^2\)\(=\)\(\cfrac{9\sqrt{3}}{4}\),当点 \(A\) 从点 \(D\) 向点 \(B\) 或点 \(C\) 运动时,三角形的面积开始减小,当到达点 \(E\) 或点 \(F\) 时,三角形变为直角三角形[此时为另一个锐角三角形和直角三角形的临界位置],此时面积为 \(\cfrac{3\sqrt{3}}{2}\),故 \(\triangle ABC\) 面积的取值范围为\((\cfrac{3\sqrt{3}}{2}, \cfrac{9\sqrt{3}}{4}]\).
【法1】: 由于 \(a=6\),设 \(b=x\),则\(c=2x\),可得\(: p=\cfrac{1}{2}(a+b+c)=3+\cfrac{3 x}{2}\)
所以 \(S=\sqrt{p(p-a)(p-b)(p-c)}=\sqrt{(3+\cfrac{3}{2}x)(\cfrac{3}{2}x-3)(3+\cfrac{1}{2}x)(3-\cfrac{1}{2}x)}\)
\(=\sqrt{[(\cfrac{3}{2}x)^2-3^2][3^2-(\cfrac{1}{2}x)^2]}=\sqrt{(\cfrac{9x^2}{4}-9)(9-\cfrac{x^2}{4})}\)
\(=\sqrt{\cfrac{81x^2}{4}-\cfrac{9x^4}{16}-81+\cfrac{9x^2}{4}}=\sqrt{-\cfrac{9}{16}x^4+\cfrac{90}{4}x^2-81}\)
\(=\sqrt{-\cfrac{9}{16}(x^4-40x^2)-81}=\sqrt{-\cfrac{9}{16}(x^4-40x^2+20^2)-81+\cfrac{9}{16}\times 20^2}\)
\(=\sqrt{225-81-\cfrac{9}{16}(x^4-40x^2+20^2)}\)\(=\sqrt{144-\cfrac{9}{16}(x^{2}-20)^{2}}\)
由三角形的三边关系可知:\(\left\{\begin{array}{l}{x+2x>6}\\{x+6>2x}\\{6+2x>x}\end{array}\right.\),解得:\(2<x<6\)
故当\(x^2=20\),即当\(x=2\sqrt{5}\in (2,6)\)时, \(S_{\triangle ABC}\)取得最大值\(12\) [1:1]
此时由\(\cfrac{1}{2}\times 2\sqrt{5}\times4\sqrt{5}\sin A=12\),解得:\(\sin A=\cfrac{3}{5}\)
解后反思:①明确海伦公式的作用,已知三边可以求解三角形的面积,或表示了三边,可以表达三角形的面积函数,从而可以求面积的最值;
②注意此题目的运算,有相当的难度,求最值时还涉及到复合函数;
③注意利用三角形的三边关系,求自变量的取值范围的技巧;
【法2】:由于\(|BC|=6\)为定值,求 \(\triangle ABC\)面积的最大值,只需要求出顶点 \(A\) 到 \(BC\) 边距离的最大值即可,注意到 \(AB=2AC\),从运动变化的视角,点 \(A\) 是运动变化的,因此有必要探索此点 \(A\) 的几何特征,即轨迹是什么。
如图,以 \(BC\) 所在的直线为 \(x\) 轴,以 \(BC\) 的中垂线为 \(y\) 轴建立直角坐标系 \(xOy\),易知点 \(B(-3,0)\), \(C(-3,0)\),
设点 \(A(x,y)\),则由 \(AB=2AC\)可得,\(\sqrt{(x+3)^2+y^2}=2\sqrt{(x-3)^2+y^2}\),
化简整理,得到 \((x-5)^2+y^2=16=4^2\),其中 \(x\neq0\),所以点 \(A\) 的轨迹是以点 \((5,0)\) 为圆心,以\(4\)为半径的圆(剔除 \(x\) 轴上的两个点),易知点 \(A\) 到 \(BC\) 边距离的最大值,即点 \(D\) 到 \(x\) 轴的距离,也即是圆的半径 \(4\) ,
故 \(\triangle ABC\) 的面积的最大值为 \(S_{\max}=\cfrac{1}{2}\times 6\times 4=12\),
此时点 \(A\) 位于 点 \(D\) 处,可知 \(AE=4\), \(BE=8\), 由勾股定理可知,\(AB=4\sqrt{5}\),同时 \(AE=4\), \(CE=2\),由勾股定理可知,\(AC=2\sqrt{5}\),
在 \(\triangle ABC\) 中,\(AB=4\sqrt{5}\),\(AC=2\sqrt{5}\),\(BC=6\),
由余弦定理可以求得,\(\cos A=\cfrac{(4\sqrt{5})^2+(2\sqrt{5})^2-6^2}{2\times4\sqrt{5}\times2\sqrt{5}}=\cfrac{4}{5}\),故 \(\sin A=\cfrac{3}{5}\) .
【非对角对边型的】