5. 线性时间排序
Method: 不通过比较数据进行排序,要求数组值在一定范围内;根据数组值的大小范围K,生成一个K大小的新数组,依序存储原数组的值的数量,最后取出新数组的内容即可。

1 public class XianxingShijianPaixu { 2 public int[] solution(int[] input, int k){ 3 int[] kElem = new int[k + 1]; 4 int n = input.length - 1; 5 int[] output = new int[n + 1]; 6 for(int i = 0; i <= n; i++){ 7 kElem[input[i]] = kElem[input[i]] + 1; 8 } 9 for(int j = 1; j <= k; j++){ 10 kElem[j] = kElem[j] + kElem[j - 1]; 11 } 12 for(int h = 0; h <= n; h++){ 13 // System.out.println(input[h]+ " h:" + h); 14 // System.out.println(kElem[input[h]]+ " h:" + h); 15 16 output[kElem[input[h]]-1] = input[h]; 17 // System.out.println(input[h]+ " h:" + h); 18 kElem[input[h]]--; 19 // System.out.println(kElem[input[h]]); 20 21 } 22 return output; 23 } 24 public static void main(String[] args){ 25 // int[] x = {1,3,4,6,57,34,23,897,567,3,2,6,10}; 26 int[] x = {2,8,7,1,3,5,6,4,0,5,3,2}; 27 // int[] x = {1,0,2}; 28 int[] y = new XianxingShijianPaixu().solution(x, 8); 29 // int[] y = new KuaiPai().secondPart(x, 0, x.length - 1); 30 System.out.println(y[5] + " " + y[6] + " "); 31 } 32 }
4. 快速排序
Method:FirstPart使用位置标记i 和 j,保证i 位置处之前的均为比array[array.length - 1]小,array[i + 1]设置为array[array.length - 1],其后均为比array大的项;SencondPart两次递归使用FirstPart实现最终排序。(可以随机选择array[array.length - 1]值,便于改善平均时间复杂度)

1 import java.util.Random; 2 3 public class KuaiPai { 4 5 int i1; 6 public int firstPart(int[] input, int p, int r){ 7 int i = p - 1; 8 int tmp = 0; 9 for(int j = p; j < r; j++){ 10 if(input[j] < input[r]){ 11 i++; 12 tmp = input[j]; 13 input[j] = input[i]; 14 input[i] = tmp; 15 } 16 } 17 tmp = input[r]; 18 input[r] = input[i + 1]; 19 input[i + 1] = tmp; 20 System.out.println(input[p] +" " + input[r]); 21 return i; 22 23 } 24 25 public int firstPartRandom(int[] input, int p, int r){ 26 Random random = new Random(); 27 int i = random.nextInt(r - p) + p; 28 int tmp = input[r]; 29 input[r] = input[i]; 30 input[i] = tmp; 31 return firstPart(input, p, r); 32 } 33 34 public int[] secondPart(int[] input, int p ,int r){ 35 // int i = 0; 36 if (p < r){ 37 i1 = firstPartRandom(input, p , r); 38 System.out.println("i1: " + i1); 39 secondPart(input, p , i1); 40 secondPart(input, i1 + 2, r); 41 } 42 return input; 43 } 44 public static void main(String[] args){ 45 int[] x = {1,3,4,6,57,34,23,897,567,3,2,6,10}; 46 // int[] x = {2,8,7,1,3,5,6,4}; 47 // int[] x = {1,0,2}; 48 // int y = new KuaiPai().firstPart(x, 0, x.length - 1 ); 49 int[] y = new KuaiPai().secondPart(x, 0, x.length - 1); 50 System.out.println(y[2] + " " + y[12] + " "); 51 } 52 }
3. 堆排序(三步排完)
Method:FirstPart假设左右两子堆是最大堆,与父堆比较生成新的一个最大堆,需要一次递归调用;SecondPart设置一个无序数组从Array.length - 1处开始调用F,保证生成一个最大堆;ThirdPart取出最大堆的最大值后,交换最后一值,调用F(array,0),完成过程。 this.arrayLength attention!

1 //import java.lang.*; 2 import java.lang.reflect.Array; 3 public class DuiPaixu { 4 int arrayLength; 5 public int[] firstPart(int[] input){ 6 int n = input.length - 1; 7 int left = 0; 8 int right = 0; 9 int max = 0; 10 for(int i = 0; i < n; i++){ 11 if( 2 * i + 2 <= n){ 12 left = input[2 * i + 1]; 13 right = input[2 * i + 2]; 14 if(left > input[i] && right > input[i]){ 15 if(left < right){ 16 max = right; 17 input[2 * i + 2] = input[i]; 18 input[i] = max; 19 20 } 21 else{ 22 max = left; 23 input[2 * i + 1] = input[i]; 24 input[i] = max; 25 } 26 } 27 else if(left > input[i]){ 28 max = left; 29 input[2 * i + 1] = input[i]; 30 input[i] = max; 31 } 32 else if(right > input[i]){ 33 max = right; 34 input[2 * i + 2] = input[i]; 35 input[i] = max; 36 } 37 } 38 if(2 * i + 2 > n && 2 * i + 1 == n){ 39 left = input[2 * i + 1]; 40 if(left > input[i]){ 41 max = left; 42 input[2 * i + 1] = input[i]; 43 input[i] = max; 44 } 45 } 46 47 } 48 return input; 49 } 50 //T(n) = O(n) no better than following. 51 52 public int[] firstPartBetter(int[] input, int i){ 53 int j = 2 * i + 1; 54 int k = 2 * i + 2; 55 int largest = 0; 56 int tmp = 0; 57 //具体情况具体写清晰 58 // this.arrayLength = input.length - 1; 59 // System.out.println(j + " k: " + k + " "+ arrayLength); 60 if(k <= arrayLength){ 61 if(input[i] < input[j]){ 62 largest = j; 63 } 64 else{ 65 largest = i; 66 } 67 if(input[k] > input[largest]){ 68 largest = k; 69 } 70 // System.out.println(largest + " i: " + i); 71 if(largest != i){ 72 tmp = input[i]; 73 input[i] = input[largest]; 74 input[largest] = tmp; 75 firstPartBetter(input, largest); 76 } 77 } 78 else if(k > arrayLength && j == arrayLength){ 79 if(input[i] < input[j]){ 80 tmp = input[i]; 81 input[i] = input[j]; 82 input[j] = tmp; 83 } 84 } 85 return input; 86 87 } 88 89 public int[] secondPart(int[] input){ 90 // this.arrayLength = input.length - 1; 91 System.out.println("test" + arrayLength); 92 for(int i = arrayLength; i >= 0; i--){ 93 // System.out.println(i); 94 firstPartBetter(input, i); 95 } 96 return input; 97 } 98 99 public int[] thirdPart(int[] input){ 100 this.arrayLength = input.length -1; 101 secondPart(input); 102 int tmp = 0; 103 for(int i = input.length - 1; i >= 0 ; i--){ 104 tmp = input[i]; 105 input[i] = input[0]; 106 input[0] = tmp; 107 this.arrayLength = this.arrayLength - 1; 108 firstPartBetter(input, 0); 109 } 110 return input; 111 } 112 113 public static void main(String[] args){ 114 int[] x = {78,34,67,89,23,2,14,6,7,3,8,8,33,3,3,1,335,7}; 115 int[] y = new DuiPaixu().thirdPart(x); 116 System.out.println(y[2] + " " + y[3]+ " " + y[17]); 117 } 118 }
2. 归并排序(分治法)
方法:FirstPart对左右各已排序完成部分进行整合排序,SecondPart对大的待排序数组进行分治操作,具体分解流程见下图,其它递归算法也可参照。
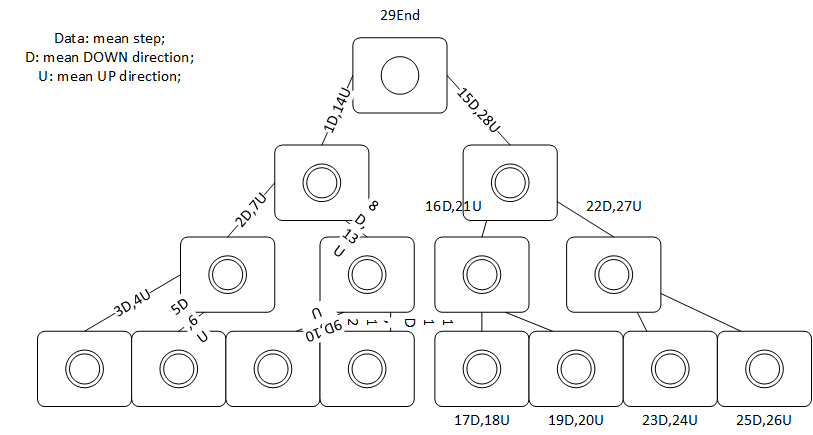

1 public class GuibingPaixu { 2 public int[] firstPart(int[] input, int p, int q, int r){ 3 int n1 = q - p + 1; 4 int n2 = r - q; 5 int k = 0; 6 int[] input1 = new int[n1]; 7 int[] input2 = new int[n2]; 8 for(int i = 0; i < n1; i++){ 9 input1[i] = input[p + i]; 10 // System.out.println(input1[i]+"/n"); 11 } 12 for(int j = 0; j < n2; j++){ 13 input2[j] = input[q + j + 1]; 14 } 15 int m = 0; 16 int n = 0; 17 while(k < n1 + n2){ 18 if(m < n1 && n < n2){ 19 if(input1[m] <= input2[n]){ 20 input[p + k] = input1[m]; 21 m++; 22 } 23 else{ 24 input[p + k] = input2[n]; 25 n++; 26 } 27 } 28 else if(m >= n1 && n < n2){ 29 input[p + k] = input2[n]; 30 n++; 31 } 32 else{ 33 input[p + k] = input1[m]; 34 m++; 35 } 36 k++; 37 } 38 return input; 39 } 40 41 public int[] secondPart(int[] input, int p, int r){ 42 int q = 0; 43 if(p < r){ 44 q = (p + r)/2; 45 secondPart(input, p, q); 46 System.out.println(q); 47 System.out.println("r:" + r); 48 secondPart(input, q + 1, r); 49 System.out.println( "right" + q + 1); 50 firstPart(input, p, q, r); 51 System.out.println( "first" + q); 52 53 } 54 return input; 55 } 56 57 58 public static void main(String[] args){ 59 int[] x = {5,7,8,9,23,56,1,2,3,4,5,6,7,89}; 60 int[] x1 = {5,1,89,3,5,8,2,0,34,12,33,445,667,6,34}; 61 int[] y = new GuibingPaixu().firstPart(x, 1, 5, 13); 62 int[] y1 = new GuibingPaixu().secondPart(x1, 0, 14); 63 System.out.println(y1[0] + " " + y1[1] + " " + y1[2] + " " + y1[14]); 64 // System.out.println(y[0] + " " + y[1] + " " + y[2] + " " + y[13]); 65 } 66 }
1. 直接插入排序
应用:属于比较排序的一种,最基础的排序方法,稳定,时间复杂度为O(n^2),空间复杂度为S(1).
方法:设置待排数字角标为i,j = i, 把j对应数字与其前的字数逐个对比交换完成后,i++即可.

1 public class Paixu { 2 public int[] paixu(int[] input){ 3 int n = input.length - 1; 4 for(int i = 1; i <= n; i++){ 5 int j = i; 6 int tmp = 0; 7 for(; j > 0 && input[j] < input[j - 1]; j--){ 8 tmp = input[j - 1]; 9 input[j - 1] = input[j]; 10 input[j] = tmp; 11 } 12 13 } 14 return input; 15 } 16 //T(n) = O(n ^ 2); S(n) = O(1) 插入排序 17 public static void main(String[] args){ 18 int[] x = {3,3,7,8,21,1}; 19 int[] y = new Paixu().paixu(x); 20 System.out.println(y[0] + " " + y[1]); 21 } 22 }
