trie

 Trie(retrieval) is an order tree data structure that is used to store “string”.

 Unlike normal tree, trie does not store data in its nodes,node position indicates what data the node associates with.

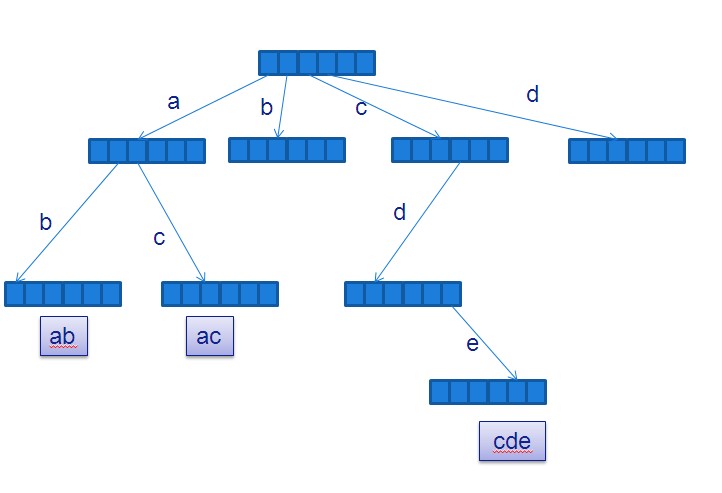
 below is what a trie looks like holding string: ab, ac,b,cd,cde,d. 

A simple definition of a trie node:

struct node
{
 Bool isWord;//is current node the last node of a word?
 node*child[26];
};

As you can see in the graph above, each edge from a node denotes a ‘letter’ (the relative position where the edge comes from indicates which letter it represents),
When traversing from root to some of its descendant with a dfs (depth first searching), we got a ‘string’.

Note that every node has unique parent, so there is always a unique path from child to the root. 

Initially, trie has a root node only. Then we insert string into it:

void insert(char*pWord)
{
 if(!pWord || *pWord == 0)
     return ;
 char* pw = pWord;
 char c = *pw++;
 node *p = root;
 while( c )
 {
   if(p->child[c] == null)
   {
      node*q = new node();
      p->child[c] = q;
   }

   P = p->child[c];
   c = *pw++;
 }

 p->isWord = true;
}

The ‘isWord’ in the node struct indicates whether path from here to the root represent a string.

This variable is of help when we need to insert strings like these: “abc”, “abcde”, whose path in the trie completely overlaps each other. 

When searching for a string, we traverse each node like this:

bool SearchWord(const char*pWord)
{
  if(!pWord || *pWord == 0)
     return false;
  char*pw = pWord;
  node*p = root;
  char c = *pw++;
  while( c )
  {
     if(p->[c] == null)
       return false;

      p = p->[c];
      c = *pw++;
   }

   return p->isWord;
}

 Above is a simple version of implementation of a trie.

 All I want to show is the idea how a trie helps searching for a string in a dictionary in an efficient way.

 Searching complexity is linear time of the length of the string being search, irrelevant to the size of the string set the trie is holding.

 Of course, setting up the trie will still cost a little, which is always an evitable operation.