P3183 [HAOI2016]食物链
题目描述
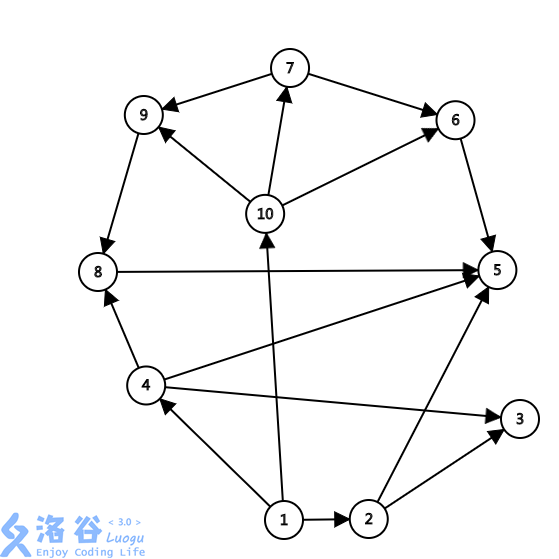
如图所示为某生态系统的食物网示意图,据图回答第1小题现在给你n个物种和m条能量流动关系,求其中的食物链条数。物种的名称为从1到n编号M条能量流动关系形如a1 b1a2 b2a3 b3......am-1 bm-1am bm其中ai bi表示能量从物种ai流向物种bi,注意单独的一种孤立生物不算一条食物链
输入格式
第一行两个整数n和m,接下来m行每行两个整数ai bi描述m条能量流动关系。(数据保证输入数据符号生物学特点,且不会有重复的能量流动关系出现)1<=N<=100000 0<=m<=200000题目保证答案不会爆 int
输出格式
一个整数即食物网中的食物链条数
输入输出样例
输入 #1
10 16
1 2
1 4
1 10
2 3
2 5
4 3
4 5
4 8
6 5
7 6
7 9
8 5
9 8
10 6
10 7
10 9
输出 #1
9
【思路】
记忆化搜索
一开始我想DP然后失败了
不过貌似记忆化搜索很好想
所以我就来尝试了一哈
没有问题
【题目大意】
有向图,找完整的链的数目
(完整的链的意思是:
链的头不能有入边,链的尾不能有出边)
【题目分析】
上面已经说过
一条完整的链就是链的头不能有入边
链的尾不能有出边
因为如果还有的话那就是还有可以被吃或者吃的
那这条食物链就没有结束
就不能算是一条食物链
(学过生物食物链那一部分知识的的应该都知道)
所以搜索的时候就有了目标
从头开始搜,因为头要满足没有入边
所以在建图的时候记录入度和出度
然后如果这个点没有入度
那就是可以搜的
但是还是有一个条件的
他必须要有出度才能搜
不然就成了一个没有入度也没有出度的点
也就是一种孤立的生物
所以必须满足没有入度并且有出度
这样同时也可以避免把孤立的生物算进来
这样搜索肯定是要超时的
所以就要考虑优化
【优化】
剪枝?不现实
没一条边都有可能参与到食物链的构建中去
所以剪枝的话没有剪枝的条件
那就记忆化搜索吧
反正每个点之后会有多少条食物链都是一定的
那就开一个数组记录每个点之后有多少条食物链
这样如果数组里面有值
那就直接加上就好了
否则就搜一下然后记录起来
【完整代码】
#include<iostream>
#include<cstdio>
#define int long long
using namespace std;
const int Max = 200005;
struct node
{
int y,ne;
}a[Max];
int head[Max >> 1],sum = 0;
void add(int x,int y)
{
a[++ sum].y = y;
a[sum].ne = head[x];
head[x] = sum;
}
int ru[Max >> 1],chu[Max >> 1];
int dp[Max >> 1];
int ans = 0;
int dfs(int x)
{
if(dp[x] != 0)return dp[x];
int ans = 0;
if(ru[x] != 0 && chu[x] == 0)
ans ++;
for(register int i = head[x];i != 0;i = a[i].ne)
{
ans += dfs(a[i].y);
}
dp[x] = ans;
return ans;
}
signed main()
{
int n,m;
cin >> n >> m;
int a,b;
for(register int i = 1;i <= m;++ i)
{
cin >> a >> b;
add(a,b);
chu[a] ++;
ru[b] ++;
}
int tot = 0;
for(register int i = 1;i <= n;++ i)
if(ru[i] == 0 && chu[i] != 0)
tot += dfs(i);
cout << tot << endl;
return 0;
}