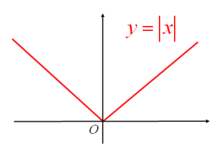
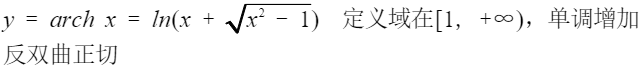绝对值函数
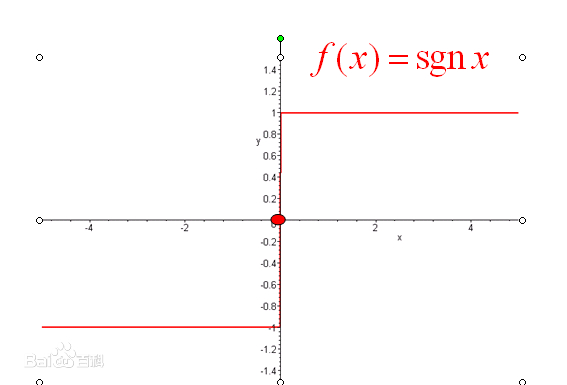
符号函数
取整函数(阶梯曲线)

函数的特性
函数有界性
- 讨论函数有界要先指明区间
- 函数f(x)在X有界的充要条件是它在X上 有上界且有下界
函数单调性
- 区间I上,x1 < x2 ,恒有 f(x1) < f(x2),则函数f(x)单调递增 (自变量差值与因变量差值同号递增)
- 区间I上,x1 < x2 ,恒有 f(x1) > f(x2),则函数f(x)单调递减 (自变量差值与因变量差值异号递减)
函数奇偶性
- f(x) = f(-x),f(x)是偶函数
- f(-x) = -f(x),且f(0) = 0,f(x)是奇函数
- F(x)=f(x) - f(-x) 是奇函数
- F(x)=f(x) + f(-x)是偶函数
- 偶函数关于y轴对称,是对关于某个轴对称的函数的平移
- 奇函数关于原点对称
- 两个偶函数的和是偶函数,两个奇函数和是奇函数
- 两个偶函数乘积是偶函数,两个奇函数乘积是偶函数,偶函数与奇函数乘积是奇函数
函数周期性
- f(x + l) = f(x) 恒成立,称 f(x) 为周期函数,l 称为f(x)的周期,一般指最小正周期
迪利克雷函数(周期函数)

这是一个周期函数,任何正有理数都是它的周期,因为不存在最小的正有理数,所以没有最小正周期
直接函数与反函数
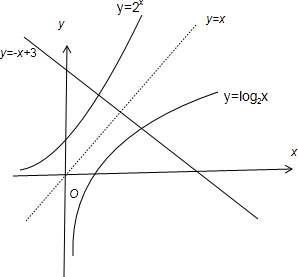
函数的运算
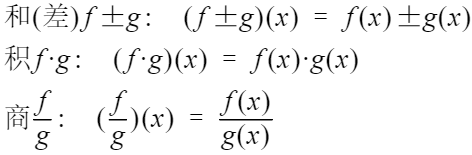
复合函数
y = f[g(x)],由函数 u = y(x)与函数y=f(u)构成的复合函数 ,有 f 。g(x) = f[g(x)]
初等函数
基本初等函数
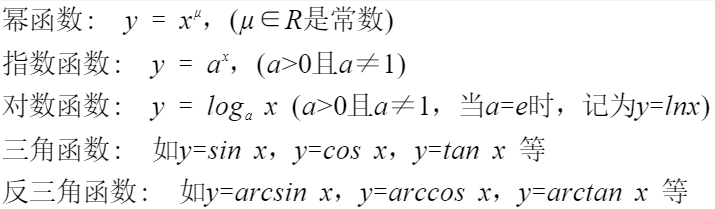
经过有限次四则运算和有限次的函数复合步骤构成并可用一个式子表示的函数,称为初等函数
双曲函数

双曲正弦,是奇函数,过原点且关于原点对称,单调增加
双曲余弦,是偶函数,通过点(0, 1)且关于y轴对称,在(-∞,0)内是单调减少的,在(0,+∞)是单调增加的,ch0 = 1是函数的最小值
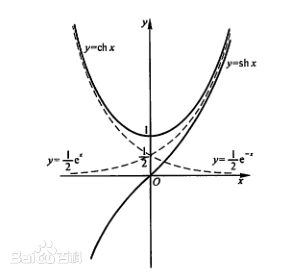
双曲正切,是奇函数,通过原点且关于原点对称,单调增加,夹在 y=1 以及 y=-1 之间,当x的绝对值足够大时,在第一象限接近于直线 y=1,在第三象限接近于直线 y=-1

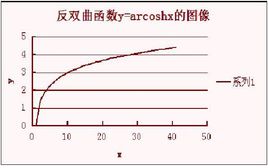
反双曲函数