几类拓扑空间的特征性质
1.子空间
对于拓扑空间$X$中的子集$A$,若对于任何从$A$到拓扑空间$Y$的连续函数$f$,都存在唯一的从$X$到$Y$连续函数$g$使得下图交换:
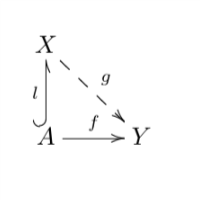
那么称$A$是$X$的一个子空间。
2.积空间
对于一族拓扑空间${X_i }_{i=1}^n $,其积空间是一个拓扑空间$Z$,满足对于任意从$Z$到任意拓扑空间$Y$的连续函数$f$和每个分量$X_i $,都存在唯一的连续函数$g_i $使得下图交换:
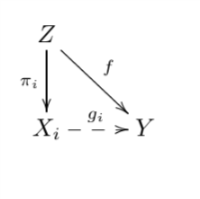
记作$prod_{alpha } X_{alpha } $
3.无交并空间
对于一族拓扑空间${X_{alpha } } $,其无交并是一个拓扑空间$Z$,满足对于任意从$Z$到$Y$的连续函数$f$和$alpha $,都存在唯一的连续函数$f_{alpha }$使下图交换:
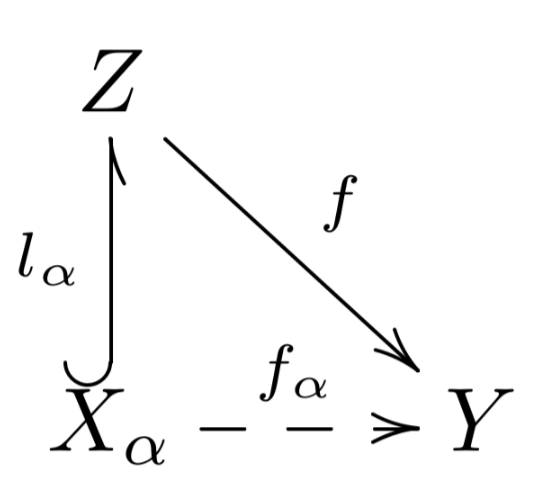
4.商空间
设$X$是一个拓扑空间,若拓扑空间$Z$满足:对任意的从$X$到$Y$的连续映射$g$,存在唯一的从$Z$到$Y$的连续映射$ ilde{g}$使得下图交换:
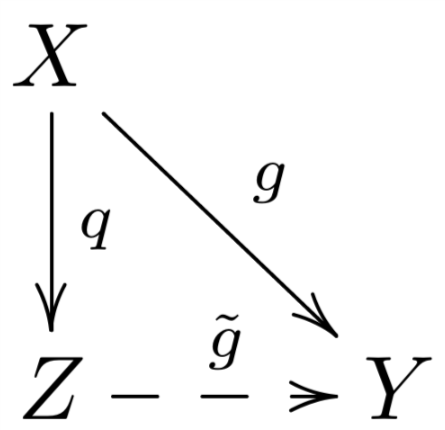
则称$Z$是$X$的商空间。