A
题目大意
在 (n×n) 的网格上放 (k) 个勇士,勇士可攻击与它相邻的 8 个格子,问有多少种放置 (k) 个勇士的方案使它们之间无法互相攻击。
解题思路
状压 DP
每个格子只有两种状态(放置棋子/不放置棋子),这我们可以用 (1/0)来表示
假设现在有一个 (3 × 3) 的网格,问放置一个棋子的方案数
那么所有合法的摆放方案可以用以下状态来表示:
① ② ③ ④ ⑤ ⑥ ⑦ ⑧ ⑨ 100
000
000010
000
000001
000
000000
100
000000
010
000000
001
000000
000
100000
000
010000
000
001接下来考虑递推公式:
定义 (cnt[j]) 表示状态 (j) 的 1 的个数
定义 (dp_{i,j,l}) 表示第 (i) 行状态为 (j) , 共放置了 (l) 个棋子的方案数
那么可以递推得到 (dp_{i,j,l} = dp[{i - 1][h][l - cnt_j]})
其中 (h) 为 (i - 1) 行的状态,且 $ j 、h $ 为合法状态 , 且 (j、h) 两种状态摆放的棋子不冲突
那么(ans = ∑dp[n][i][k])
AC_Code
#include<bits/stdc++.h>
#define int long long
#define rep(i , a , b) for(int i = a ; i <= b ; i ++)
using namespace std;
const int N = 3e5 + 10;
int n , k , cnt[N] , dp[11][1 << 11][110];
vector<int>vec; // 储存合法状态
int calc(int x) // 统计二进制中 1 的个数
{
int res = 0;
while(x)
{
if(x & 1) res ++ ;
x >>= 1;
}
return res;
}
bool check(int x) //判断状态 x 是否合法
{
rep(i , 0 , n)
{
if((x >> i & 1) && (x >> (i + 1) & 1)) return false;
}
return true;
}
bool ok(int i , int j) // 判断 i , j 俩状态是否冲突
{
if((i & j) || (i >> 1 & j) || (j >> 1 & i)) return false;
return true;
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0) , cout.tie(0);
cin >> n >> k;
int sum = (1 << n) - 1;
rep(i , 0 , sum) if(check(i))
{
if(cnt[i] > k) continue ;
cnt[i] = calc(i);
vec.push_back(i);
}
for(auto i : vec) dp[1][i][cnt[i]] = 1;
rep(i , 2 , n) for(auto j : vec)
for(auto h : vec)
{
if(!ok(j , h)) continue ;
rep(l , 0 , k)
{
if(l < cnt[j]) continue ;
dp[i][j][l] += dp[i - 1][h][l - cnt[j]];
}
}
int ans = 0;
for(auto i : vec) ans += dp[n][i][k];
cout << ans << '
';
return 0;
}
B
题目大意
有 $ N $ 堆砖头从左向右摆在一条线上。第(i)堆砖头所在的坐标为(Xi), 它的高度为(Hi).
现在可以使用一种炸弹把这些砖头炸碎。在坐标(X)上使用 (1) 次炸弹会将所有处于 (X-D) 到 (X+D) (包含端点) 的所有砖头的高度减少 (A)
现在希望用尽量少的炸弹来把所有摆出来的砖都炸掉,请计算最少用几次炸弹。
解题思路
将 (N) 堆砖头按照坐标 (Xi) 从小到大排序,然后开始贪心
如何贪心呢?首先观察性质不难发现 , 要将所有砖头的高度炸为 (0) , 最左边的砖头高度也必然要炸为 (0). 而要将最左边的砖头的高度炸为 (0),必然只有一个最优的方案:在 (X1 + D) 的位置安放炸弹直到最左边的砖头高度被炸为 (0) , 然后再查找下一个最左边的高度不为 (0) 的砖头,重复上述操作直到所有砖头高度都为 (0)
简略证明一下方案可行性:
定义高度大于 (0) 的最左边的砖头坐标为 X
那么要使炸弹可以炸到 (X) ,则安置炸弹的范围必须为 ([X-D,X+D])
其中将炸弹安置在 (X+D) 可以炸到的范围为 ([X,X+2×D]) , 其余安置点的爆炸范围为 ([Y,Y+2×D]) ((Y < X))
因为 (X) 的左边已经不存在高度大于 (0) 的砖头了,所以其余安置点的有效爆炸范围为 ([X,Y+2×D]), 小于([X,X+2×D])
所以将炸弹安置在 (X+D) 一定最优,贪心方案可行
那么怎么写呢?
通过上述我们可以发现我们需要实现两个操作
1.区间修改 (将区间内每个数的值都减少 A)
2.查询左边第一个下标大于 (0) 的砖头
操作 ① 很显然用线段树跑一跑就好了, 操作 ② 也就在线段树上跑个二分就好了
由于 (X) 的范围很大线段树存不下,所以需要离散化坐标 (X)
AC_Code
#include<bits/stdc++.h>
#define rep(i , a , b) for(int i = a ; i <= b ; i ++)
#define int long long
#define ll long long
using namespace std;
const ll INF (0x3f3f3f3f3f3f3f3fll);
const int N = 2e5 + 10;
struct Tree
{
ll l,r,sum,lazy,maxn;
} tree[2000000];
void push_up(ll rt)
{
tree[rt].sum=tree[rt<<1].sum+tree[rt<<1|1].sum;
tree[rt].maxn=max(tree[rt<<1].maxn,tree[rt<<1|1].maxn);
}
void push_down(ll rt , ll length)
{
if(tree[rt].lazy)
{
tree[rt<<1].lazy+=tree[rt].lazy;
tree[rt<<1|1].lazy+=tree[rt].lazy;
tree[rt<<1].sum+=(length-(length>>1))*tree[rt].lazy;
tree[rt<<1|1].sum+=(length>>1)*tree[rt].lazy;
tree[rt<<1].maxn+=tree[rt].lazy;
tree[rt<<1|1].maxn+=tree[rt].lazy;
tree[rt].lazy=0;
}
}
void build(ll l , ll r , ll rt , ll *aa)
{
tree[rt].lazy=0 , tree[rt].l=l , tree[rt].r=r;
if(l==r)
{
tree[rt].sum=aa[l] , tree[rt].maxn=tree[rt].sum;
return;
}
ll mid=(l+r)>>1;
build(l,mid,rt<<1,aa);
build(mid+1,r,rt<<1|1,aa);
push_up(rt);
}
void update_range(ll L , ll R , ll key , ll rt)
{
if(tree[rt].r<L||tree[rt].l>R)return;
if(L<=tree[rt].l&&R>=tree[rt].r)
{
tree[rt].sum+=(tree[rt].r-tree[rt].l+1)*key;
tree[rt].maxn+=key;
tree[rt].lazy+=key;
return;
}
push_down(rt,tree[rt].r-tree[rt].l+1);
ll mid=(tree[rt].r+tree[rt].l)>>1;
if(L<=mid)update_range(L,R,key,rt << 1);
if(R>mid)update_range(L,R,key,rt << 1 | 1);
push_up(rt);
}
ll query_range(ll L, ll R, ll rt)
{
if(L<=tree[rt].l&&R>=tree[rt].r) return tree[rt].sum;
push_down(rt,tree[rt].r-tree[rt].l+1);
ll mid=(tree[rt].r+tree[rt].l)>>1;
ll ans=0;
if(L<=mid)ans+=query_range(L,R,rt << 1);
if(R>mid)ans+=query_range(L,R,rt << 1 | 1);
return ans;
}
ll query_max(ll L, ll R, ll rt)
{
if(L<=tree[rt].l&&R>=tree[rt].r) return tree[rt].maxn;
push_down(rt,tree[rt].r-tree[rt].l+1);
ll mid=(tree[rt].r+tree[rt].l)>>1;
ll ans=-(0x3f3f3f3f3f3f3f3fll);
if(L<=mid)ans=max(ans,query_max(L,R,rt << 1));
if(R>mid)ans=max(ans,query_max(L,R,rt << 1 | 1));
return ans;
}
ll query_range_size(ll L , ll R , ll rt , ll val)
{
if(tree[rt].l == tree[rt].r)
return tree[rt].l;
push_down(rt,tree[rt].r-tree[rt].l+1);
ll mid = tree[rt].l + tree[rt].r >> 1;
if(tree[rt << 1].maxn > val) return query_range_size(L , R , rt << 1 , val);
else if(tree[rt << 1 | 1].maxn > val) return query_range_size(L , R , rt << 1 | 1 , val);
else return -1;
}
struct node
{
int x , h;
bool operator < (const node & b) const {
return x < b.x;
}
} a[N];
ll n , d , c , ans , ha[N] , dist[N];
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0) , cout.tie(0);
cin >> n >> d >> c;
rep(i , 1 , n)
{
cin >> a[i].x >> a[i].h;
ha[i] = a[i].h;
}
sort(a + 1 , a + 1 + n);
rep(i , 1 , n) ha[i] = a[i].h , dist[i] = a[i].x;
ha[n + 1] = INF , dist[n + 1] = INF , a[n + 1].x = INF;
build(1 , n , 1 , ha);
rep(i , 1 , n)
{
ll now = query_range_size(i , n , 1 , 0);
if(now == -1) continue;
ll h = query_range(now , now , 1);
ll cal = h / c;
if(h % c) cal ++;
int cnt = upper_bound(dist + 1 , dist + n + 2 , a[now].x + d * 2) - dist;
update_range(now , cnt - 1 , -(cal * c) , 1);
ans += cal;
}
cout << ans << '
';
return 0;
}
C
题目大意
给定一个含有 (n) 个整数的数组a,将其所有点对((i,j),i≠j),两两相乘 (a[i]×a[j]) 得到 (N(N−1)/2) 个数,问将其升序排序后第 (k) 个数是多少?
解题思路
分类讨论 (+) 尺取 (+) 二分
很显然可以将两两相乘的结果分为三类
- 正数 × 负数
- 零 × 负数,零 × 正数
- 负数 × 负数,正数 × 正数
记负数的个数为 (f) , 零的个数为 (z),正数的个数为 (c)
那么负数的下标区间为 ([1,f]) , 零的下标区间为 ([f + 1 , f + c]) , 正数的下标区间为 ([f + c + 1 , n])
那么第一类的总数为 (f×c),第二类的总数为 (z×f + z×c),第三类的总数为 (f×(f-1)/2 + c×(c-1)/2)
然后我们先对所有数从小到大排个序 , 再根据 K 的大小进行分类讨论:
第一类
很显然是从区间 ([-INF,-1]) 二分答案 (mid)
但是如何 (check) 呢?
不难想到 (mid) 一定是由一个正数 × 一个负数构成
于是可以采用尺取法统计小于等于 (mid) 的数的个数int pos = n - c + 1 , sum = 0; rep(i , 1 , f) { while(pos <= n && a[i] * a[pos] > mid) pos ++; if(pos <= n && a[i] * a[pos] <= mid) sum += n - pos + 1; }当然如果你觉得尺取法不太好写 or 代码量太大,也是可以采用 lower_bound 来计算的
int sum = 0; rep(i , 1 , f) { int x = mid / a[i]; if(mid % a[i]) x ++; int cnt = lower_bound(a + 1 , a + 2 + n , x) - a; if(cnt > n) continue ; sum += n - cnt + 1; }我们只要判断 (k >= sum) 是否成立即可写出 (check)
第二类
直接输出 (0) 即可
第三类
同第一类一样从区间 ([1,INF]) 二分答案 (mid)
但构成的方式有两种会相对复杂一些
1.负数 × 负数 2.正数 × 正数
不过大体思路和第一类差不多,就不细讲了
AC_Code
#include<bits/stdc++.h>
#define int long long
#define rep(i , a , b) for(int i = a ; i <= b ; i ++)
#define per(i , b , a) for(int i = b ; i >= a ; i --)
using namespace std;
const int INF (0x3f3f3f3f3f3f3f3fll);
const int N = 2e5 + 10;
int a[N] , b[N] , d[N];
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0) , cout.tie(0);
int n , k;
int z = 0 , f = 0 , c = 0 , ans;
cin >> n >> k;
rep(i , 1 , n)
{
cin >> a[i];
if(!a[i]) z ++ ;
else if(a[i] > 0) c ++ ;
else f ++ ;
}
sort(a + 1 , a + 1 + n);
a[n + 1] = INF;
if(k <= f * c)
{
int l = -INF , r = -1 , mid;
while(l <= r)
{
mid = l + r >> 1LL;
int sum = 0;
rep(i , 1 , f)
{
int x = mid / a[i];
if(mid % a[i]) x ++;
int cnt = lower_bound(a + 1 , a + 2 + n , x) - a;
if(cnt > n) continue ;
sum += n - cnt + 1;
}
if(sum >= k) r = mid - 1 , ans = mid;
else l = mid + 1;
}
cout << ans << '
';
}
else if(k > z * (z - 1) / 2 + f * c + z * f + z * c)
{
k -= z * (z - 1) / 2 + f * c + z * f + z * c;
int l = 1 , r = INF , mid , cnt = 0;
rep(i , 1 , f)
b[i] = -a[f - i + 1];
rep(i , f + z + 1 , n)
d[++ cnt] = a[i];
while(l <= r)
{
mid = l + r >> 1;
int sum = 0 , pos = f;
rep(i , 1 , f)
{
if(b[i] * b[i] <= mid) sum -- ;
while(b[i] * b[pos] > mid && pos) pos -- ;
if(pos && b[i] * b[pos] <= mid) sum += pos;
}
pos = c;
rep(i , 1 , c)
{
if(d[i] * d[i] <= mid) sum -- ;
while(d[i] * d[pos] > mid && pos) pos -- ;
if(pos && d[i] * d[pos] <= mid) sum += pos;
}
if(sum / 2 >= k) r = mid - 1 , ans = mid ;
else l = mid + 1;
}
cout << ans << '
';
}
else cout << 0 << '
';
return 0;
}
D
题目大意
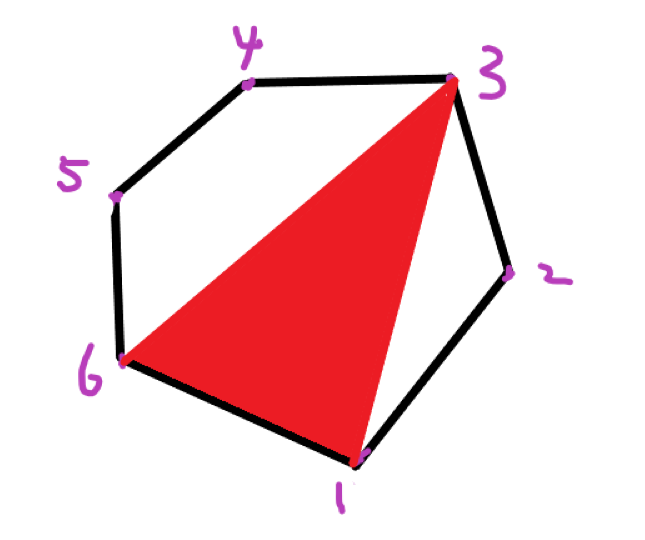
给定一个具有 (N) 个顶点的凸多边形,将顶点从 (1) 至 (N) 标号,每个顶点的权值都是一个正整数。
将这个凸多边形划分成 (N-2) 个互不相交的三角形,对于每个三角形,其三个顶点的权值相乘都可得到一个权值乘积
问所有三角形的顶点权值乘积之和最少为多少。
解题思路
区间 DP
将每个顶点进行编号(从 (1 - n)),第 (i) 个顶点的权值为 (ai)
定义 (dp_{i,j}) :将顶点 (i-j) 所构成的多边形划分成不相交三角形所得到的最小权值乘积
那么不难得到状态转移方程: (dp_{i,j} = dp_{i,k} + dp_{k,j} + a_i×a_j×a_k) (见下图)
AC_Code
#include<bits/stdc++.h>
#define int long long
#define rep(i , a , b) for(int i = a ; i <= b ; i ++)
using namespace std;
const int INF = 0x3f3f3f3f33fll;
const int N = 1e2 + 10;
int n , a[N] , dp[N][N];
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0) , cout.tie(0);
cin >> n;
rep(i , 1 , n) cin >> a[i];
for(int len = 2 ; len <= n ; len ++)
{
for(int l = 1 ; l + len <= n ; l ++)
{
int r = l + len;
dp[l][r] = INF;
rep(k , l , r - 1) dp[l][r] = min(dp[l][r] , dp[l][k] + dp[k][r] + a[l] * a[k] * a[r]);
}
}
cout << dp[1][n] << '
';
return 0;
}
E
F
题目大意
给定 (N) 个灯,每个灯都有两种状态(开/关)
第 (i) 个灯的编号为 (i),起初所有灯都是亮的
现在有 (k) 次操作,每次操作给定一个数 (x) 要求把编号为 (x) 的倍数的灯的状态改变 ( 开 → 关,关 → 开)
问整个过程中灯最多关闭了几盏
解题思路
作为签到题,它的考点为 调和级数的复杂度
for(int i = 1 ; i <= n ; i ++) for(int j = 1 ; j <= n ; j += i)for(int i = 1 ; i <= n ; i ++) for(int j = 1 ; i * j <= n ; j ++)在知道以上复杂度为 (nlogn) 后 ,再按题意模拟一遍即可
AC_Code
#include<bits/stdc++.h>
#define rep(i , a , b) for(int i = a ; i <= b ; i ++)
using namespace std;
const int N = 1e6 + 10;
int a[N];
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0) , cout.tie(0);
int n , sum = 0 , ans = 0;
cin >> n;
rep(i , 1 , n) a[i] = 1;
int k;
cin >> k;
while(k --)
{
int x;
cin >> x;
for(int i = x ; i <= n ; i += x)
{
if(a[i]) sum ++ ;
else sum --;
a[i] ^= 1;
}
ans = max(ans , sum);
}
cout << ans << '
';
return 0;
}
G
题目大意
给定一个包含 (N) 个数的集合,求这个集合的 (MEX)
$ MEX $ 的定义:集合中未出现的最小自然数
解题思路
(N) 的范围貌似没给 ?但 (N) 给不给其实也无所谓
题目给定的集合内元素的范围是 (-10^{100})~(10^{100})
显然这个范围的元素用整型变量是无法直接储存的,于是读入要用字符串来操作
而一共就 (N) 个元素,那么 (MEX) 必然出现在 (0) ~ (N) 之中
所以当读入的字符串的长度是否大于 (logN) 时直接跳过对这个数的操作
当读入的字符串长度小于等于 (logN) 时,将其转换为数字并存入该数字对应的桶中(桶 = 数组)
最后从 (0) ~ (N) 遍历所有桶,找到第一个空桶输出其编号即可
AC_Code
#include<bits/stdc++.h>
#define rep(i , a , b) for(int i = a ; i <= b ; i ++)
using namespace std;
const int N = 2e6 + 10;
char s[N];
int n , cnt[N];
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0) , cout.tie(0);
cin >> n;
rep(i , 1 , n)
{
cin >> s;
if(s[0] == '-') continue ;
int m = strlen(s);
if(m > 6) continue ;
int x = atoi(s);
cnt[x] ++ ;
}
rep(i , 0 , n) if(!cnt[i]) return cout << i << '
' , 0;
return 0;
}