@description@
给定有一个 n*n 的平原,其中一些格子有些泉水。泉水每单位时间生产的水量有多有少。
平原周围有 4*n 头大象,如下图所示的绿色部分。大象可以将鼻子笔直伸向自己面对的方向喝泉水(假设鼻子长到可以触碰对面边缘),如下图所示红色线段。
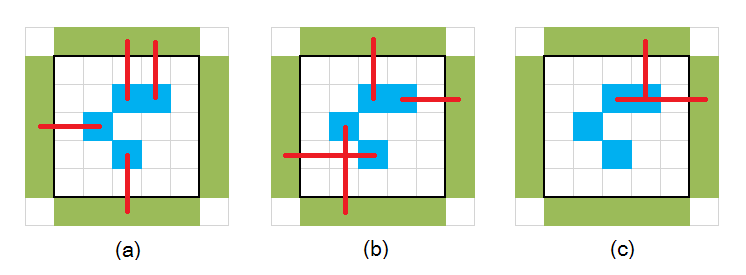
本题还有些额外限制:大象的鼻子不能相交;每个泉水最多被一个大象占领。如图 (a) 是合法的,图 (b) 都算大象的鼻子相交。
请计算大象们每单位时间最多能喝多少的水。
Class:
ElephantDrinking
Method:
maxSum
Parameters:
String[]
Returns:
int
Constraints
n 在 2 到 50 之间。通过字符串数组来描述平原,其中字符串 i 的第 j 位为一个 '0'~'9' 的数,描述平原 (i, j) 的单位时间产水量(0 则不产水)。
Examples
0)
{"00000",
"00110",
"01000",
"00100",
"00000"}
Returns: 4
1)
{"111",
"191",
"111"}
Returns: 16
@solution@
这个 dp。。。虽然不难理解。。。但是好像有点乱搞。。。
(注:以下的图片都不是我画的,是从其他地方截下来的)
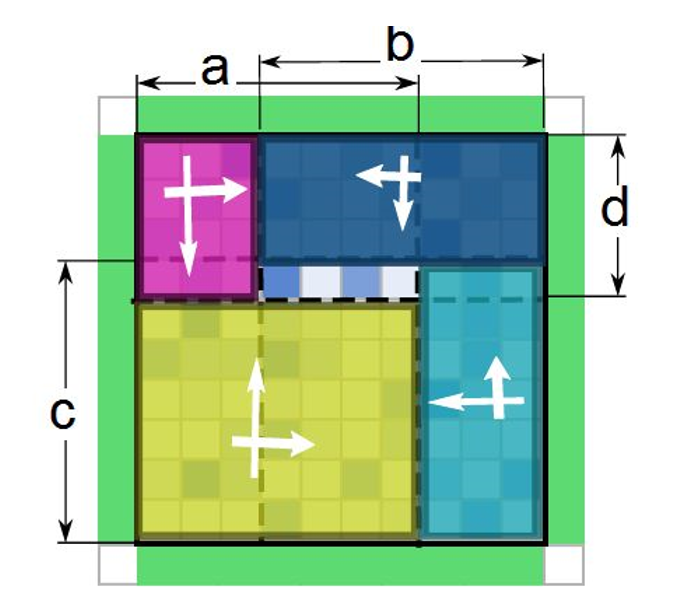
首先我们令 a 表示最左面的大象的鼻子向右最远延伸到多少行,同理定义 b 表示最右,c 表示最下,d 表示最上。
考虑如果 a <= b,实际上中间形成了一条可以供上下的大象自由伸展鼻子的区域(如下图)。

我们假设预处理出 f[i][j] 表示仅考虑左大象和上大象时,取矩阵左上部分到 (i, j) 这一区域的最优答案。同理再预处理出仅考虑左、下;仅考虑右、上;仅考虑右、下的值。
则上图中蓝、黄、青、紫区域的答案就是我们预处理出来的值。
橙色区域实际上每一列只会有两头大象,所以处理出每一列的最大值与次大值之和即可。
如果 d <= c,其实就是把上下变成了左右,一样的处理即可。
如果 a > b 且 d > c,实际上形成了像是弦图的模样(如下图):

只需要枚举中间那个空的矩形即可,一样利用我们预处理好的信息。
当然它还可以转个方向(如下图),不过处理方法还是一样:
现在考虑怎么预处理出 f[i][j] 呢?这里仅说明左、上的情况,其他情况类似。
我们枚举最后一行的大象鼻子延伸的位置;再枚举一列,使那一列上面的大象鼻子延伸至最后一行,且那一列左边没有任何大象延伸至最后一行。枚举的那一列右边的大象没有限制,故肯定延伸至最大泉水处。
这样总时间复杂度就是 O(n^4) 的,可以很轻松地跑过。
@accepted code@
#include<cstdio>
#include<vector>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
const int MAXN = 50;
class ElephantDrinking{
public:
int a[MAXN + 5][MAXN + 5], n;
int tmp[MAXN + 5], res;
int f1[MAXN + 5][MAXN + 5];
void get_lu() {
for(int j=1;j<=n;j++) tmp[j] = 0;
memset(f1, 0, sizeof f1);
for(int i=1;i<=n;i++) {
for(int j=1;j<=n;j++) {
tmp[j] = max(tmp[j], a[i][j]);
for(int k=0;k<=j;k++) {
res = a[i][k], f1[i][j] = max(f1[i][j], res + f1[i-1][j]);
for(int l=j;l>k;l--)
res += tmp[l], f1[i][j] = max(f1[i][j], res + f1[i-1][l-1]);
}
// printf("* %d %d : %d
", i, j, f1[i][j]);
}
}
}
int f2[MAXN + 5][MAXN + 5];
void get_ld() {
for(int j=1;j<=n;j++) tmp[j] = 0;
memset(f2, 0, sizeof f2);
for(int i=n;i>=1;i--) {
for(int j=1;j<=n;j++) {
tmp[j] = max(tmp[j], a[i][j]);
for(int k=0;k<=j;k++) {
res = a[i][k], f2[i][j] = max(f2[i][j], res + f2[i+1][j]);
for(int l=j;l>k;l--)
res += tmp[l], f2[i][j] = max(f2[i][j], res + f2[i+1][l-1]);
}
// printf(". %d %d : %d
", i, j, f2[i][j]);
}
}
}
int f3[MAXN + 5][MAXN + 5];
void get_ru() {
for(int j=1;j<=n;j++) tmp[j] = 0;
memset(f3, 0, sizeof f3);
for(int i=1;i<=n;i++) {
for(int j=n;j>=1;j--) {
tmp[j] = max(tmp[j], a[i][j]);
for(int k=n+1;k>=j;k--) {
res = a[i][k], f3[i][j] = max(f3[i][j], res + f3[i-1][j]);
for(int l=j;l<k;l++)
res += tmp[l], f3[i][j] = max(f3[i][j], res + f3[i-1][l+1]);
}
// printf("? %d %d : %d
", i, j, f3[i][j]);
}
}
}
int f4[MAXN + 5][MAXN + 5];
void get_rd() {
for(int j=1;j<=n;j++) tmp[j] = 0;
memset(f4, 0, sizeof f4);
for(int i=n;i>=1;i--) {
for(int j=n;j>=1;j--) {
tmp[j] = max(tmp[j], a[i][j]);
for(int k=n+1;k>=j;k--) {
res = a[i][k], f4[i][j] = max(f4[i][j], res + f4[i+1][j]);
for(int l=j;l<k;l++)
res += tmp[l], f4[i][j] = max(f4[i][j], res + f4[i+1][l+1]);
}
// printf("! %d %d : %d
", i, j, f4[i][j]);
}
}
}
int solve1() {
int ret = 0, res1 = 0, res2 = 0, res3 = 0, mx = 0, smx = 0;
for(int i=0;i<=n;i++) {
res1 = res2 = 0;
for(int k=1;k<=n;k++)
res1 = max(res1, a[k][i] + f1[k-1][i] + f2[k+1][i]);
for(int j=i+1;j<=n+1;j++) {
res3 = 0;
for(int k=1;k<=n;k++)
res3 = max(res3, a[k][j] + f3[k-1][j] + f4[k+1][j]);
ret = max(ret, res1 + res2 + res3);
if( j == n + 1 ) break;
mx = smx = 0;
for(int k=1;k<=n;k++) {
if( a[k][j] > mx )
smx = mx, mx = a[k][j];
else if( a[k][j] > smx )
smx = a[k][j];
}
res2 += (mx + smx);
}
}
return ret;
}
int solve2() {
int ret = 0, res1 = 0, res2 = 0, res3 = 0, mx = 0, smx = 0;
for(int i=0;i<=n;i++) {
res1 = res2 = 0;
for(int k=1;k<=n;k++)
res1 = max(res1, a[i][k] + f1[i][k-1] + f3[i][k+1]);
for(int j=i+1;j<=n+1;j++) {
res3 = 0;
for(int k=1;k<=n;k++)
res3 = max(res3, a[j][k] + f2[j][k-1] + f4[j][k+1]);
ret = max(ret, res1 + res2 + res3);
if( j == n + 1 ) break;
mx = smx = 0;
for(int k=1;k<=n;k++) {
if( a[j][k] > mx )
smx = mx, mx = a[j][k];
else if( a[j][k] > smx )
smx = a[j][k];
}
res2 += (mx + smx);
}
}
return ret;
}
int solve3() {
int ret = 0;
for(int i=1;i<n;i++)
for(int j=i+1;j<=n;j++)
for(int k=1;k<n;k++)
for(int l=k+1;l<=n;l++) {
ret = max(ret, f1[i][l-1] + f2[i+1][k] + f3[j-1][l] + f4[j][k+1]);
ret = max(ret, f1[j-1][k] + f2[j][l-1] + f3[i][k+1] + f4[i+1][l]);
}
return ret;
}
int maxSum(vector<string>field) {
n = field.size();
memset(a, 0, sizeof a);
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
a[i + 1][j + 1] = field[i][j] - '0';
get_lu(), get_ld(), get_ru(), get_rd();
return max(max(solve1(), solve2()), solve3());
}
}ED;
@details@
写得来,但就是想不到。。。
写的时候 Ctrl + c 与 Ctrl + v 用得很爽 2333。