随机梯度下降
影响搜索全局最小值的因素
1.局部最小值
可能在进行梯度下降的时候,初始化的时候离其中一个局部最小值比较接近,于是最终的结果可能就会收敛在这个局部最小值。
2.鞍点
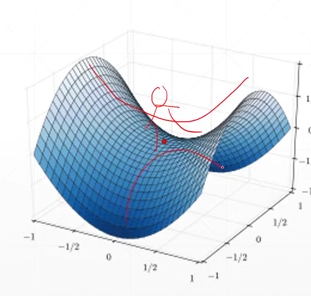
就是从一个方向进行梯度下降的话,它会找到一个局部最小值(图中的红点),而从另外一个方向的话会找到一个局部最大值,而都不是全局最小值。
3.初始状态
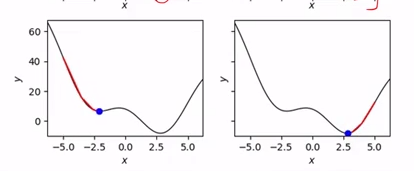
如图,如果初始化的点在图的左边的话,可能最后收敛的点就是-2.5的局部极小值,而如果初始化的点在图右边的话,可能收敛的点就是2.5 全局最小值
4.学习率
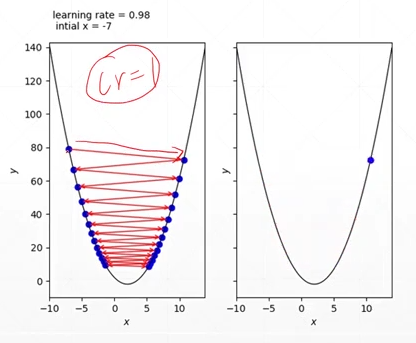
可能学习率过大的话,你的收敛过程会不断地在全局极小值点附近震动而无法得到最优解。 所以就需要进行一个learning rate的衰减,在快收敛的时候减小learning rate。
5.动量(如何逃离局部极小值)
原理就是当你暂时陷入一个局部极小值的话,通过这个惯性可以冲出局部极小值继续向下进行梯度下降。
求导数的方法

autograd.grad()函数
计算导数
例子:
import torch
import torch.nn.functional as F
x = torch.ones(1)
w = torch.full([1],2,requires_grad=True)#这里不加requires_grad=True的话会报错RuntimeError: element 0 of tensors does not require grad and does not have a grad_fn
mse = F.mse_loss(x*w,torch.ones(1))#第一个参数是prediction,第二个参数是label
print(mse)#均方差loss输出为1
print(torch.autograd.grad(mse,[w]))#对loss求关于w的偏导
输出:
tensor(1., grad_fn=<MseLossBackward>)
(tensor([2.]),)
loss.backward()函数
计算计算图中的各个参数的导数,并将相应参数的导数信息自动附加在 参数.grad 属性中。
例子:
import torch
import torch.nn.functional as F
x = torch.ones(1)
w = torch.full([1],2,requires_grad=True)#这里不加requires_grad=True的话会报错RuntimeError: element 0 of tensors does not require grad and does not have a grad_fn
mse = F.mse_loss(x*w,torch.ones(1))#第一个参数是prediction,第二个参数是label
mse.backward()
print(w.grad)
#输出为tensor([2.])