作者在Slimmable Neural Networks这篇文章中研究了训练宽度可实时变化的网络的方法,但那篇文章中的宽度是训练时指定好的固定的宽度。在这篇文章中作者提出一种训练universally slimmable networks(USNet)的方法,运行时可以选择某个范围中的任意宽度,并且作者说明这种方法还可以用于训练nonuniform USNet即各层拥有不同比例的宽度。
神经网络$y=sum_{i=1}^{n}w_ix_i$可以看作是feature aggregation的过程,每一个输入神经元都负责detect某一个特征,而输出神经元则通过可学习的transformation整合特征。因此更宽的网络至少可以达到比较窄的网络的表现,因为至少可以保持前面channel的权重新增channel权重为零。所以网络的残差error是有上下限的,$|y^n-y^{k+1}|leqslant |y^n-y^k|leqslant |y^n-y^{k_0}|$,这说明训练的好的网络不管是否有BN层,取其中的任意宽度都是可以使用的。在本文中作者提出了训练USNet的两个技巧(三明治法则,原地蒸馏),并且解决了BN层的问题。
Post-Statistics Batch Normalization
SNet中提出了BN层在Slimmable中会存在的问题,解决方法是采用switchable batch normalization,也就是对子网络采取单独的BN层。但这样的解决方法有两个问题:
- 全部子网络在训练时都统计单独的BN数据计算量很大而且低效
- 如果每次迭代只想更新其中的一些子网络,那么这些BN数据就没有充分累积也就不准确了。
因此本文中提出了Post-Statistics BN的方法。不同宽度的BN层数据在训练后进行计算,BN层中的参数共享。而且文中实验了四种计算BN statistics的方法:在完整训练集上计算moving average;在整个训练集上计算exact average;选取训练集中的1k数据计算exact average;选取2k数据计算exact average。发现当weight固定后这4中方法计算得到的表现都很接近。
Sandwich Rule
训练一个USNet一个方法是同SNet一样累积或者平均不同子网络的loss。但通过上下限的公式,可以得知每个子网络的表现可以通过优化上下限得到优化。因此本文中提出,每一轮迭代时选取网络最小宽度,最大宽度和$n-2$个随机宽度进行训练。
文中在$n=3$时实验4种网络宽度的选取方案:3个随机宽度;最小宽度+2个随机宽度;最大宽度+2个随机宽度;最大宽度+最小宽度+1个随机宽度。发现不同宽度平均表现最好的是最大宽度+最小宽度+随机宽度的训练方案,其次是最小宽度+2个随机宽度。实验发现下限的优化对训练比较重要。
还选取了$n=3, 4, 5$进行了实验,发现$n=4$比$n=3$效果要好,和$n=5$很接近。当$n$增大,训练时间是要明显增大的,所以后续$n$设定为4.
Inplace Distillation
Sandwich Rule的训练方式天然地适合知识蒸馏,可以将最大宽度的模型地predicted label作为其他模型地training label,最大宽度则使用groundtruth。在实际操作时需要注意不要将最大宽度的预测结果的gradient传回全图。作者尝试了将groundtruth和predicted label都作为training label,不论使用constant balance还是decaying balance结果都worse。
完整的算法流程如下:

其他实验
对于ImageNet,MobileNet-v1 Slimmable训练得到的子网络比直接训练的相同宽度的网络表现要好,MobileNet-v2(是residual net)比单独的要差。
US-WDSR比WDSR要差约0.01PSNR,但目前default的超参可能不利于US-WDSR。
还实验证明了这种方式也可以应用于强化学习。
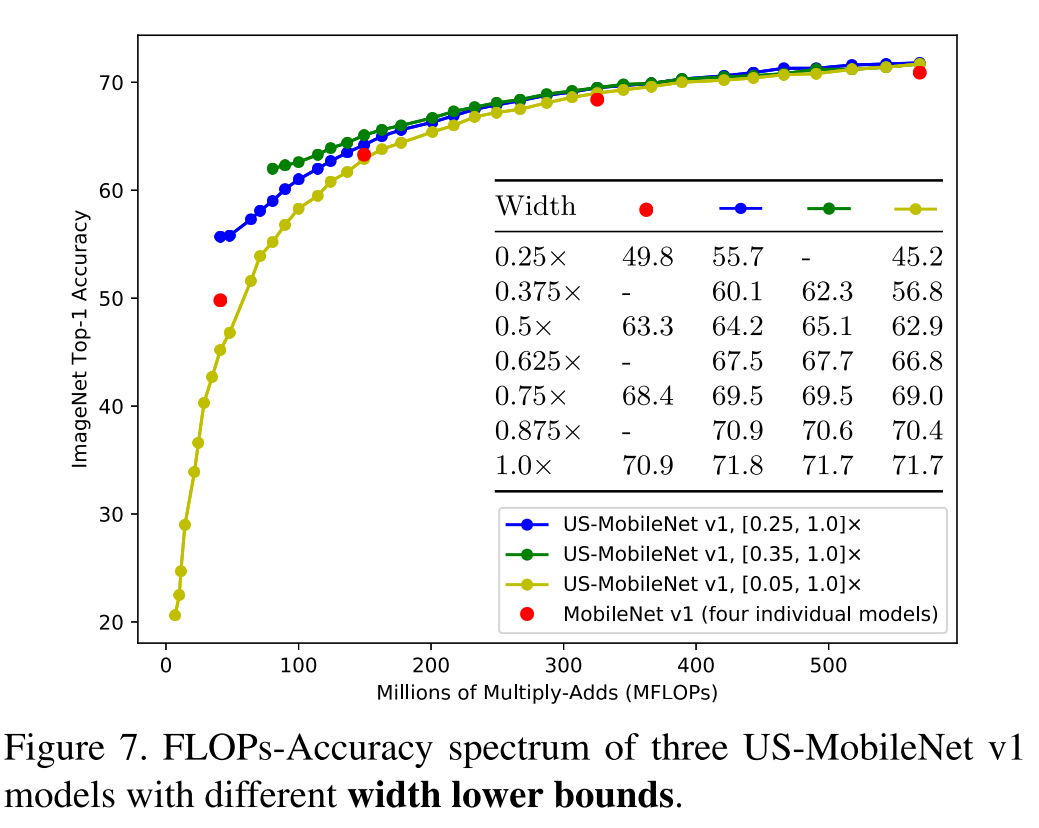
最小宽度$k_0$的选择:训练了三个US-MobileNet-v1,$k_0=0.25, 0.35, 0.05$.说明US-Net的表现是受$k_0$影响的,而且当使用的宽度越小这个影响越大。
最小的宽度调整单位d:实验发现最小的调整尺度设为8比设为1表现要略好一点,并且由于硬件原因,在矩阵乘法中矩阵的大小是8的倍数是运算比较快。