codeforces 515B.Drazil and His Happy Friends

B. Drazil and His Happy Friends

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Drazil has many friends. Some of them are happy and some of them are unhappy. Drazil wants to make all his friends become happy. So he invented the following plan.

There are n boys and m girls among his friends. Let's number them from 0 to n - 1 and 0 to m - 1 separately. In i-th day, Drazil invites 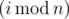-th boy and 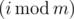-th girl to have dinner together (as Drazil is programmer, i starts from 0). If one of those two people is happy, the other one will also become happy. Otherwise, those two people remain in their states. Once a person becomes happy (or if he/she was happy originally), he stays happy forever.

Drazil wants to know whether he can use this plan to make all his friends become happy at some moment.

Input

The first line contains two integer n and m (1 ≤ n, m ≤ 100).

The second line contains integer b (0 ≤ b ≤ n), denoting the number of happy boys among friends of Drazil, and then follow b distinct integers x1, x2, ..., xb (0 ≤ xi < n), denoting the list of indices of happy boys.

The third line conatins integer g (0 ≤ g ≤ m), denoting the number of happy girls among friends of Drazil, and then follow g distinct integers y1, y2, ... , yg (0 ≤ yj < m), denoting the list of indices of happy girls.

It is guaranteed that there is at least one person that is unhappy among his friends.

Output

If Drazil can make all his friends become happy by this plan, print "Yes". Otherwise, print "No".

Sample test(s)

input

2 3
0
1 0

output

Yes

input

2 4
1 0
1 2

output

No

input

2 3
1 0
1 1

output

Yes

Note

By 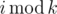 we define the remainder of integer division of i by k.

In first sample case:

• On the 0-th day, Drazil invites 0-th boy and 0-th girl. Because 0-th girl is happy at the beginning, 0-th boy become happy at this day.
• On the 1-st day, Drazil invites 1-st boy and 1-st girl. They are both unhappy, so nothing changes at this day.
• On the 2-nd day, Drazil invites 0-th boy and 2-nd girl. Because 0-th boy is already happy he makes 2-nd girl become happy at this day.
• On the 3-rd day, Drazil invites 1-st boy and 0-th girl. 0-th girl is happy, so she makes 1-st boy happy.
• On the 4-th day, Drazil invites 0-th boy and 1-st girl. 0-th boy is happy, so he makes the 1-st girl happy. So, all friends become happy at this moment.

n个男孩，m个女孩，假如他们之间约会无限次，我们就会发现约会分成了gcd(m,n)组。只要每组有至少1人快乐，那么在有限的步数下，整个组都会快乐，于是，我们只要分好组，然后找组内是否有人快乐。

#include<iostream>
#include<algorithm>
#include<cstring>
#include<iomanip>
#include<cctype>
#include<string>
#include<cmath>
#include<cstdio>
#include<cstdlib>
#define LL long long
#define PF(x) ((x)*(x))
#define LF(x) ((x)*PF(x))

using namespace std;
const int INF=1<<31-1;
const int max9=1e9;
const int max6=1e6;
const int max3=1e3;

int gcd(int a,int b)
{
    return b==0?a:gcd(b,a%b);
}
int t1[120];
int t2[120];

int main()
{
    int n,m;
    while(cin >> n >> m)
    {
        memset(t1,0,sizeof(t1));
        memset(t2,0,sizeof(t2));
        int x;
        int temp;
        cin >> x;
        while(x--)
        {
            cin >> temp;
            t1[temp]=1;
        }
        cin >> x;
        while(x--)
        {
            cin >> temp;
            t2[temp]=1;
        }
        int w=gcd(n,m);
        int s=n/w*m;
        int flag;
        for(int i=0;i<w;i++)
        {
            flag=0;
            for(int j=i;j<s;j+=w)
            {
                if(t1[j%n]) flag=1;
                if(t2[j%m]) flag=1;
                if(flag) break;
            }
            if(flag==0) break;
        }
        if(flag) cout << "Yes" << endl;
        else cout << "No" << endl;
    }
    return 0;
}