题目:UOJ#201。
题目大意:给定n个点(n是偶数)的完全图,现在要你给每条边确定一个权值(互不相等),使得最长的单调上升路径最短。现在要你输出边的权值。
一条路径被称为单调上升的,如果沿着它走时的权值是单调递增的。
解题思路:题目中的证明告诉我们一个结论:单调上升路径至少为n-1。
所以我们要让这个单调上升路径长度为n-1。
一张n个点的完全图可以拆成n-1个互不相等的,每个点的度数都为1的子图。例如
而每个这样的子图都走一条边,则刚好n-1。
那么我们对这样的一张子图,使它的所有边权值连续即可。
那么如何构造这样的图呢?
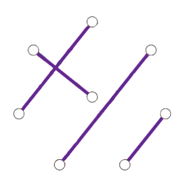
把这张子图的边转一下,点不变,就是一张新的、边不重复的子图。
所以如此构造出子图即可。
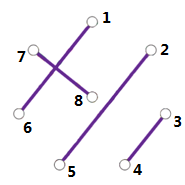
我的编号方法如下图,每次旋转时,点$a$对应的另一个点$p_a$就改为$(p_a+1)mod(n-1)+1$即可(与中间的点n有关的点有一些不同,见代码)。
C++ Code:
#include<cstdio>
#include<cstring>
int n,p[505],num=0;
int e[505][505];
int main(){
memset(e,0,sizeof e);
scanf("%d",&n);
for(int i=1;i<=n;++i)p[i]=n+1-i;
for(int i=1;i<=n;++i)if(!e[i][p[i]])e[i][p[i]]=e[p[i]][i]=++num;
for(int i=2;i<n;++i){
for(int j=1;j<n;++j){
if(i==j)p[j]=n;else
if(p[j]==n){
p[j]=(j+1)%(n-1)+1;
}else
p[j]=(p[j]+1)%(n-1)+1;
}
p[n]=i;
for(int j=1;j<=n;++j)if(!e[j][p[j]])e[j][p[j]]=e[p[j]][j]=++num;
}
for(int i=1;i<n;++i){
for(int j=i+1;j<n;++j)printf("%d ",e[i][j]);
printf("%d
",e[i][n]);
}
return 0;
}