卡特兰数

卡特兰数

• 通项公式1：(h(n) = frac{1}{n + 1}C_{2n}^n = C_{2n}^n - C_{2n}^{n - 1})
• 通项公式2：(h(n) = frac{1}{n + 1}sum_{i = 0}^n(C_n^i)^2)
• 递推公式1：(h(n) = frac{4n - 2}{n + 1}h(n), h(0) = 1)
• 递推公式2：(h(n + 1) = sum_{i = 0}^nh(i)h(n - i),h(0) = 1)

问题：从((0,0))到((n,n))，每次只能向右或向上走，且不能超过对角线，求走法个数

进出栈 - 括号匹配

有n个数字顺序入栈，求有几种进出栈的顺序

电影购票

电影票50元，如果有m + n个人排队买票，其中m个人各持有50元面值的钞票1张，而另外n个人各持有100元面值的钞票1张。票房没有预备找零，求有多少种方法可以将这m + n个人排成一列，顺序购票，使得都能买到票

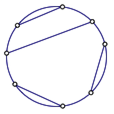
圆内连弦

圆周上有2n个点，以这些点为端点连互不相交的n条弦，求不同的连法总数

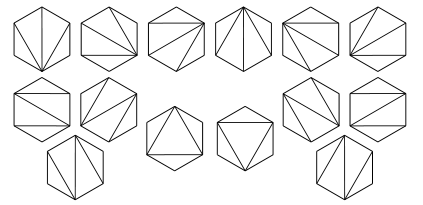
凸多边形的剖分

求凸(n + 2)变形用其(n - 1)条对角线分割为互不重叠的三角形的分法总数

模板

#include <iostream>
#include <cstdio>
#define ll long long
using namespace std;
const int N = 1e5 + 5;
const int mod = 998244353;
ll h[N], inv[N];
void solve(int N, int p){
    h[0] = 1;
    inv[1] = 1;
    for(int i = 2; i <= N; ++ i)
        inv[i] = (ll)(p - p / i) * inv[p % i] % p;//加上p为了防止变成负数
    
    for(int i = 1; i <= N; i++)
        h[i] = h[i - 1] * (4 * i - 2) % mod * inv[i + 1] % mod;
}
int main(){
    int t, n;
    cin >> t;
    solve(N - 1, mod);
    for(int i = 1; i <= t; i++){
        scanf("%d", &n);
        printf("Case #%d: %lld
", i, h[n]);
    }
    return 0;
}