题意:问1~n这n个数中,选三个各不相同的数构成三角形,有多少种方案
上图找规律:
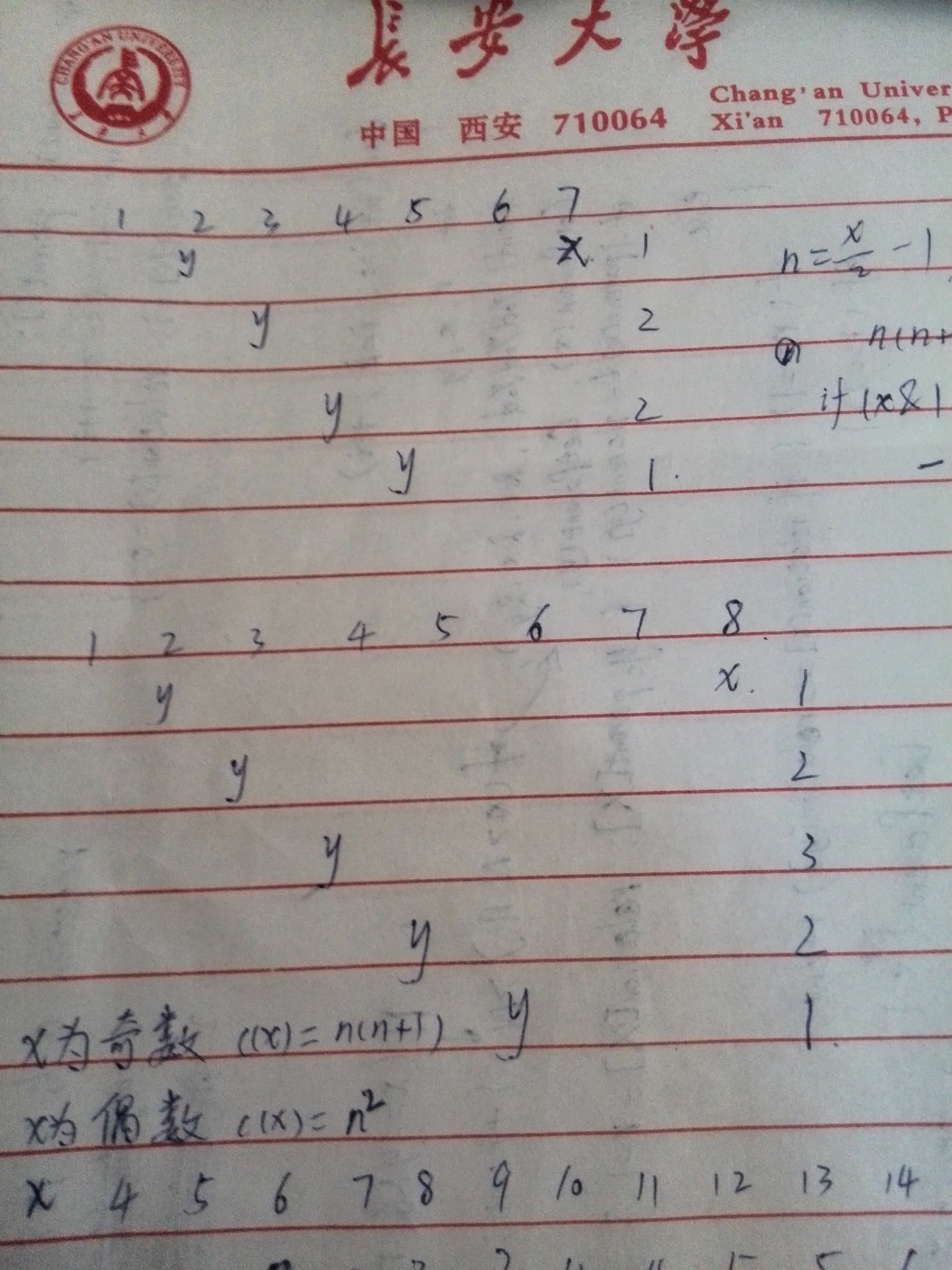
不妨设y<z<x,而且满足z>x-y,即两边之差小于第三边
图中列举了,x等于7和x等于8的情况
那么y从2开始枚举,最右边是z的方案数
我们把对应x的方案数叫做c(x),所求即是c(x)前若干项和。c(7)是从1加到n再从n加到1,是两个等差数列的和
c(8)也类似,不过那个3只有一个
找到规律:
令n=x/2-1
- x为奇数,c(x)=n(n+1)
- x为偶数,c(x)=n2
然后用递推,求出f[x] = f[x-1] + c(x)

1 //#define LOCAL 2 #include <iostream> 3 using namespace std; 4 5 long long f[1000000 + 10]; 6 7 int main(void) 8 { 9 #ifdef LOCAL 10 freopen("11401in.txt", "r", stdin); 11 #endif 12 13 f[3] = 0; 14 for(long long x = 4; x <= 1000000; ++x) 15 { 16 long long n = (x>>1) - 1; 17 if(x&1) 18 f[x] = f[x-1] + n*(n+1); 19 else 20 f[x] = f[x-1] + n*n; 21 } 22 int n; 23 while(scanf("%d", &n) == 1) 24 { 25 if(n < 3) break; 26 printf("%lld ", f[n]); 27 } 28 return 0; 29 }
好了,既然我们求出了每一项的表达式,为何不一鼓作气,求出前n项和,然后直接计算呢,这样连数组都用不到了

x为奇数时,f[x]为图中所写公式,x为偶数时,将加号改为减号即可

1 //#define LOCAL 2 #include <iostream> 3 using namespace std; 4 5 int main(void) 6 { 7 #ifdef LOCAL 8 freopen("11401in.txt", "r", stdin); 9 #endif 10 11 long long x; 12 while(scanf("%lld", &x) == 1) 13 { 14 if(x < 3) break; 15 long long n = x/2 -1; 16 if(x & 1) 17 cout << n*(n+1)*(2*n+1)/3 + n*(n+1)/2 << endl; 18 else 19 cout << n*(n+1)*(2*n+1)/3 - n*(n+1)/2 << endl; 20 } 21 return 0; 22 }
