论文来源:NIPS2011
- 相比于其它的无监督学习算法,Sparse filtering并不是去学习数据的分布,它是去分析特征的分布,良好的特征分布满足一定的特性,有了这个思想,只需要优化简单的目标函数,下面介绍。Sparse filtering可以有效地学习高维输入的特征,当进行分层训练时,Sparse filtering可以运用贪婪的思想进行训练,比如先进行第一层的训练,再进行第二层的训练,每一层都有自己的目标函数。
- Sparse filtering还有个优点是需要调的参数只有特征的维度。
- 这篇论文其实主要就包括两个部分,一是什么样的特征是好的特征,二是如何利用这个思想构造目标函数。
什么样的特征是好的特征
满足三个特性的特征是好特征,下面介绍。
Population Sparsity
sparse features per example,每个样本应该只被少数的特征激活。sparse filtering的结果如下图。
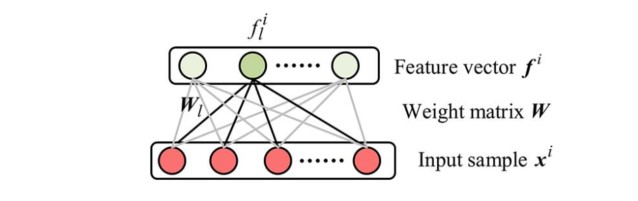
类似于一层的神经网络,但是不同的是没有偏置项。我们的输出矩阵(f_j^i)表示第i个样本在第j个特征处的激活值,那么由Population Sparsity的思路我们希望,第i列就尽可能多的零值,只有少部分特征被激活。
Lifetime Sparsity
特征应该是具有分辨能力的,因此每个特征应该只被部分样本激活。这意味着,特征矩阵的每一行拥有尽可能多的零值。
High Dispersal
直观上理解,每个特征都不应该比其它特征拥有更多的激活值。即特征的地位是均等的。这些思想来源于神经科学。
如何设计目标函数
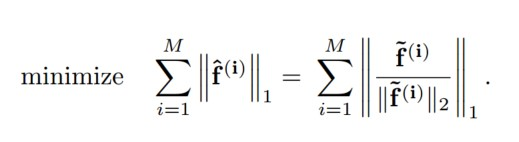
如上便是目标函数。其中
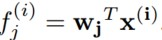

首先对特征进行给规范化,使用L2范数,其次对每个样本进行规范化,仍然使用L2范数。结果用L1范数进行约束。对所有的样本进行求和,即得到的目标函数。下面解释这样的目标函数满足特征的三个特性。
目标函数满足特征三要素
满足polulation sparsity
观察目标函数,对每个样本先L2规范化,再L1规范化,L2使得某个特征值增大,其余均减小,某个特征值减小,其余均增大。L1的最小化,要求特征值绝大多数的值尽可能接近于0。结合L1和L2的特点,使得特征值在大多数维度为0,在某些不为0的维度尽可能的大。满足了popylation sparsity条件。
满足high dispersal

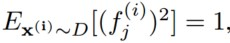
对每个维度特征的L2规范化,使得每个特征的平方期望都为1,这样实现了每个特征被同等地激活。
满足lifetime sparsity
满足population sparstity说明每个样本中的大部分特征为0,满足high dispersal说明这些0被均等地分布在各个特征中。于是对于每个特征中激活或者未激活的个数基本是均等的,这就满足了lifetime sparsity。
Matlab代码如下:
