后缀数组-----倍增算法

　　今天看了一下后缀数组算法，感觉好NB的样子，的确不太好看~~，可能智商捉急吧~~

　　后缀是字符串 r 从第 i 个字符开始到字符串结尾，后缀表示为 suffix(i)。

　　后缀数组：sa是一个一位数组，保存1...n的某个排列sa[1],sa[2],...,sa[n]，并且保证后缀从小到大进行排序之后把排序好的后缀的开头位置依次放入sa中。

　　名次数组：名次数组Rank[i]保存的是suffix[i]在所有后缀中从小到大排列中的名次。

　　后缀数组-------排第几的是谁，名次数组------你排第几。

　　倍增算法：对每个字符开始的长度为2^k的子字符串进行排序，求出排名。k从0开始，每次加1，当2^k大于n之后-----Rank值中没有相同的值，结束。每一次排序都利用上次长度为2^k-1的字符串的Rank值，那么长度为2^k的字符串就可以用两个长度为2^k-1的字符串的排名作为关键字表示，然后进行基数排序。

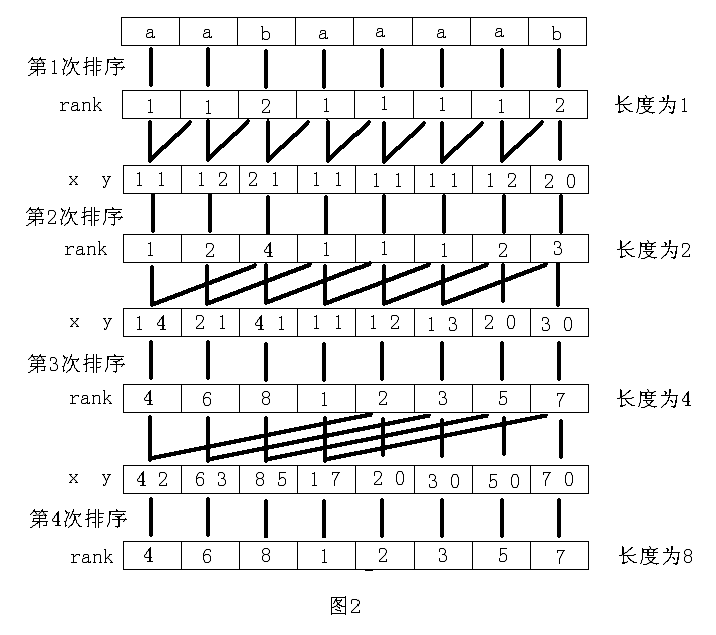
　　　　以字符串“aabaaaab”为例，整个过程如图2 所示。其中x、y 是表示长度为2k 的字符串的两个关键字。

int wa[maxn],wb[maxn],wv[maxn],ws[maxn];
int cmp(int *r,int a,int b,int l)
{return r[a]==r[b]&&r[a+l]==r[b+l];}
void da(int *r,int *sa,int n,int m)
{
int i,j,p,*x=wa,*y=wb,*t;
for(i=0;i<m;i++) ws[i]=0;
for(i=0;i<n;i++) ws[x[i]=r[i]]++;
for(i=1;i<m;i++) ws[i]+=ws[i-1];
for(i=n-1;i>=0;i--) sa[--ws[x[i]]]=i;
for(j=1,p=1;p<n;j*=2,m=p)
{
for(p=0,i=n-j;i<n;i++) y[p++]=i;
for(i=0;i<n;i++) if(sa[i]>=j) y[p++]=sa[i]-j;
for(i=0;i<n;i++) wv[i]=x[y[i]];
for(i=0;i<m;i++) ws[i]=0;
for(i=0;i<n;i++) ws[wv[i]]++;
for(i=1;i<m;i++) ws[i]+=ws[i-1];
for(i=n-1;i>=0;i--) sa[--ws[wv[i]]]=y[i];
for(t=x,x=y,y=t,p=1,x[sa[0]]=0,i=1;i<n;i++)
x[sa[i]]=cmp(y,sa[i-1],sa[i],j)?p-1:p++;
}
return;
}

函数第一步是对长度为1的字符串进行排序。一般来说，在字符串的题目中，r的值不会很大，所以这里用了基数排序。如果r的值很大，就把这段代码改成快速排序。代码：

for(i=0;i<m;i++) ws[i]=0;
for(i=0;i<n;i++) ws[x[i]=r[i]]++;
for(i=1;i<m;i++) ws[i]+=ws[i-1];
for(i=n-1;i>=0;i--) sa[--ws[x[i]]]=i;