排序二叉树

注：我已对本文章进行了更新，深入谈讨了完全二叉树的实现原理，劳烦移步。

属性：

①若它的左子树不为空，则左子树上所有节点的值均小于它的根节点的值。

②若它的右子树不为空，则右子树上所有节点的值均大于它的根节点的值。

③它的左、右子树也都是排序二叉树。

添加操作：

当根节点为空时，添加进的节点作为根节点。然后每次添加节点时，都从根节点过滤，以根节点作为当前节点，如果新节点大于当前节点，则走当前节点的右子节点分支，如果新节点小于当前节点，则走当前节点的左子节点分支。然后再用右子节点或左子节点作为当前节点与新加节点比较，如果新加节点大，则当前节点的右子节点，如果新加节点小，则当前节点的左子节点。依次类推知道左子树或右子树为null时，将该新节点添加在这里。

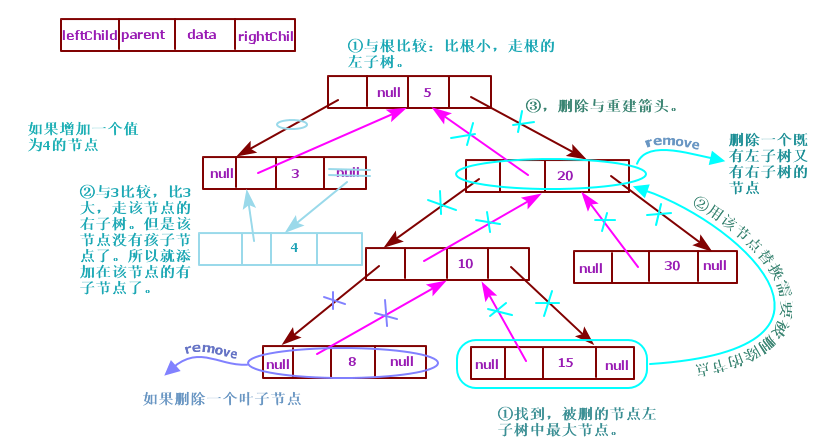
package tree;
import java.util.ArrayDeque;
import java.util.ArrayList;
import java.util.List;
import java.util.Queue;
public class SortedBinaryTree<T extends Comparable> {
    
    public static class Node<E>{
        E data;
        Node<E> parent;
        Node<E> left;
        Node<E> right;
        
        public Node() {}
        public Node(E data){
            this.data=data;
        }
        public Node(E data,Node<E> left,Node<E> right){
            this.data=data;
            this.left=left;
            this.right=right;
        }
        public Node(E data,Node<E> parent,Node<E> left,Node<E> right){
            this.data=data;
            this.parent=parent;
            this.left=left;
            this.right=right;
        }
        public boolean equals(Object obj){
            if(this==obj){
                return true;
            }else if(this.getClass()==obj.getClass()){
                Node<E> nodeObj=(Node<E>) obj;
                return nodeObj.data.equals(data) && nodeObj.left==left && nodeObj.right==right;                    
            }
            return false;
        }
        public String toString(){
            return "[data="+data+"]";
        }
    }
    private Node<T> root;
    public SortedBinaryTree() {
        root=null;
    }
    public SortedBinaryTree(T data){
        root=new Node<T>(data);
    }
    
    //往排序二叉树中添加节点
    public void add(T element){
        Node<T> node=new Node<T>(element);
        if(root==null){
            root=node;
        }else {
            Node<T> current=root;
            Node<T> parent=null;
            int cmp=0;
            //循环找到可以被添加到的位置。
            while(current!=null){
                parent=current;
                cmp=element.compareTo(current.data);
                //如果新节点大于当前节点
                if(cmp>0){
                    //以右子节点作为当前节点
                    current=current.right;
                }else {
                    current=current.left;
                }
            }
            //如果新节点大于父节点的值
            if(cmp>0){
                //新节点作为父节点的右子节点。
                parent.right=node;
            }else {
                parent.left=node;
            }
            node.parent=parent;
        }
    }
    //删除节点
    public void remove(T data){
        //获取要删除的节点
        Node<T> node=getNode(data);
        if(node==null){
            return;
        }
        boolean isLeftOfParent=isLeft(node);
        //如果删除的是叶子节点
        if(node.left==null && node.right==null){
            //如果该叶子节点就是根节点,即该树中只有一个根节点
            if(node==root){
                root=null;
            }else if(isLeftOfParent){//被删除的节点是父节点的左子节点。
                node.parent.left=null;//将被删除的节点的父节点的左子节点指针设为null
            }else {
                node.parent.right=null;
            }
            //将被删除节点的父节点指针设为null
            node.parent=null;
        }else if(node.left!=null && node.right==null){//左子树不为空，右子节点为空
            //被删除节点是根节点
            if(root==node){
                root=node.left;
            }else    if(isLeftOfParent){
                node.parent.left=node.left;            
            }else {
                node.parent.right=node.left;                
            }
            node.parent=null;
        }else if(node.left==null && node.right!=null){
            if(node==root){
                root=node.right;
            }else if(isLeftOfParent){
                node.parent.left=node.right;
            }else {
                node.parent.right=node.right;
            }
            node.parent=null;
        }else {
            Node<T> leftMaxNode=node.left;
            while(leftMaxNode.right!=null){
                leftMaxNode=leftMaxNode.right;
            }
            if(node!=root){            
                leftMaxNode.parent=node.parent;
                if(isLeftOfParent){//如果被删的节点是其父节点的左子节点，则重构其父节点的左子节点为leftMaxNode节点
                    node.parent.left=leftMaxNode;
                }else {//如果被删的节点是其父节点的右子节点，则重构其父节点的右子节点为leftMaxNode节点
                    node.parent.right=leftMaxNode;
                }
            }else {//如果删除的节点就是根节点，则重构根节点为leftMaxNode，因为一颗树必须有根节点，以如中根节点分析
                root=leftMaxNode;
            }
            if(leftMaxNode!=node.left){//>必须判断<以图中节点10分析。
                //如果leftMaxNode节点就是其根结点的左子节点，就不能有下面的语句，否则会出现死循环
                leftMaxNode.left=node.left;
                //如果leftMaxNode节点就是其根结点的左子节点，就不能有下面的语句，否则删除其他的数据-->leftMaxNode.parent.right。
                leftMaxNode.parent.right=null;
            }        
            
            leftMaxNode.right=node.right;        
            node.parent=node.left=node.right=null;
        }
    }
    private boolean isLeft(Node<T> node) {
        if(node==root){
            return false;
        }else {
            return node==node.parent.left;
        }    
    }
    public Node<T> getNode(T data) {
        Node<T> node=root;
        while(node!=null){
            int comp=data.compareTo(node.data);
            if(comp>0){
                node=node.right;
            }else if(comp<0){
                node=node.left;
            }else {
                return node;
            }
        }
        return null;
    }
    //广度优先遍历
    public List<Node<T>> breadthFirst(){
        Queue<Node<T>> queue=new ArrayDeque<Node<T>>();
        List<Node<T>> list=new ArrayList<Node<T>>();
        Node<T> tmp;
        if(root!=null){
            queue.offer(root);
        }
        while(!queue.isEmpty()){
            list.add(queue.peek());
            tmp=queue.poll();
            if(tmp.left!=null){
                queue.offer(tmp.left);
            }
            if(tmp.right!=null){
                queue.offer(tmp.right);
            }
        }
        return list;
    }
    //中序遍历
    public List<Node> midIterator(){
        return midIterator(root);
    }
    private List<Node> midIterator(Node root) {
        List<Node> list=new ArrayList<Node>();
        if(root==null){
            return null;
        }else{
            if(root.left!=null){
                list.addAll(midIterator(root.left));
            }
            list.add(root);
            if(root.right!=null){
                list.addAll(midIterator(root.right));
            }
            return list;
        }
    }
}

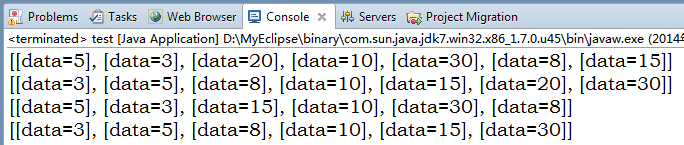
测试：

    public static void main(String[] args) {
        SortedBinaryTree<Integer> sortedBinaryTree=new SortedBinaryTree<Integer>();
        sortedBinaryTree.add(5);
        sortedBinaryTree.add(20);
        sortedBinaryTree.add(10);
        sortedBinaryTree.add(3);
        sortedBinaryTree.add(8);
        sortedBinaryTree.add(15);
        sortedBinaryTree.add(30);
        System.out.println(sortedBinaryTree.breadthFirst());
        System.out.println(sortedBinaryTree.midIterator());
        sortedBinaryTree.remove(20);
        System.out.println(sortedBinaryTree.breadthFirst());
        System.out.println(sortedBinaryTree.midIterator());
    }