二叉树他们都需要满足一个基本性质--即树中的任何节点的值大于它的左子节点,且小于它的右子节点。按照这个基本性质使得树的检索效率大大提高。我们知道在生成二叉树的过程是非常容易失衡的,最坏的情况就是一边倒(只有右/左子树),这样势必会导致二叉树的检索效率大大降低(O(n)),所以为了维持二叉树的平衡,大牛们提出了各种实现的算法,如:AVL,SBT,伸展树,TREAP ,红黑树等等。
平衡二叉树必须具备如下特性:它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。也就是说该二叉树的任何一个等等子节点,其左右子树的高度都相近。
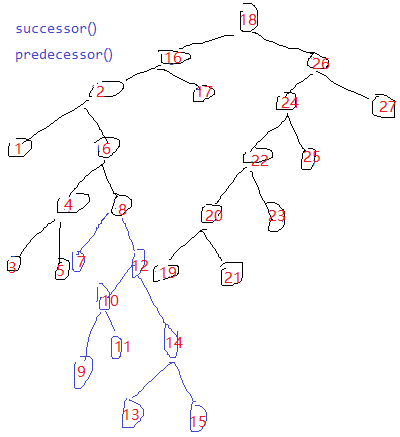
两个节点要想可达必须是父子关系。 从根节点到任一节点只有一条路径。 一个节点只有一个父节点多个子节点。一个节点的所有父节点路径是唯一的。
任何一个节点只有一个父节点,从下往上走只有一条路径,其他节点在这个路径上就可以到达,不在路径上的节点就到达不了,每一层在这个路径上的只有一个节点。
二分查找的查找效率高于顺序查找,但不适合插入。
要支持高效的插入操作,我们似乎需要一种链式结构。
单链接的链表是无法使用二分查找的,因为二分查找的高效来自于能够快速通过索引取得任何子数组的中间元素。为了将二分查找的效率和链表的灵活性结合起来,我们需要更加复杂的数据结构。
能够同时拥有两者的就是二叉查找树BST。
交换所有节点的左右子树:

public class InvertBinaryTree { //交换所有节点 public TreeNode invertTree(TreeNode root) { if (root != null) { TreeNode t = root.left;// 交换根 root.left = root.right; root.right = t; invertTree(root.left);// 交换左子树 invertTree(root.right);// 交换右子树 return root; } else { return null; } } // 层序遍历 public TreeNode invertTree_bfs(TreeNode root) { if (root == null) { return null; } else { Queue<TreeNode> queue = new LinkedList<TreeNode>(); queue.offer(root); while (!queue.isEmpty()) { TreeNode p = queue.poll(); TreeNode t = p.left; p.left = p.right; p.right = t; if (p.left != null) { queue.offer(p.left); } if (p.right != null) { queue.offer(p.right); } } return root; } } }
public class TreeNode { public int val; public TreeNode left; public TreeNode right; public TreeNode(int x) { val = x; } public TreeNode(int val, TreeNode left, TreeNode right) { super(); this.val = val; this.left = left; this.right = right; } public TreeNode() { super(); } }
二叉排序树也叫二叉搜索树也叫Binary Sort Tree也叫Binary Search Tree也叫BST
具有如下性质:
定义空树是一个BST
左子树所有结点的值均小于根结点的值
右子树所有结点的值均大于根结点的值
左右子树都是BST(递归定义)
中序遍历序列为升序
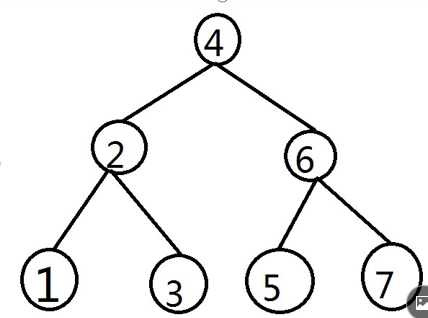
依次插入4、2、6、2、1、3、5、1、7:
插入4根节点直接插入,插入2小于4在左边,插入6大于4在右边,插入2小于4在左边,在和4的左边2比较,相等不用插入,插入1小于4在左边,左边有2,小于2在2的左边,插入3小于4在左边,大于2在右边,5大于4在右边,5小于6在左边,1小于4在左边,1小于2在左边,有一个1相等就不动,7大于4大于6.
键值对的插入:
依次插入{4:a},{2:b},{6:c},{2:d},{1:a},{3:d},{5:e},{1:f}
{2:d}替换{2:b},{1:f}替换{1:a}
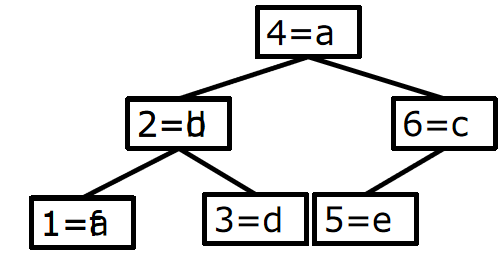
二叉搜索树Binary Search Tree BST:一边大一边小。
AVL:一边大一边小,同时左右子树高度差只能为0,1。解决了二叉搜索树的极端条件就是成为链表。
红黑树:RedBlackTree、RBT。AVL树的调整需要左右旋转,AVL的查找效率高但是插入和删除效率低,就出现红黑树。
1.红黑树不像AVL一样,永远保持绝对平衡
2.相对平衡
3.若H(left)>=H(right),则:H(left)<=2*H(right)+1,但BH(left)===BH(right)黑高相等,H(left)<H(right)同理
4.定理:N个节点的RBT,最大高度是2log(N+1),严格证明参考CLRS
5.查询效率RBT低于AVL
6.插入、删除效率好于AVL
红黑树是平衡二叉树,平衡儿茶B树,本质是一课B-tree。小的在一边大的在另一边,为了防止都是小的变成链表,所以要平衡。
AVL是通过高度实现的平衡,SBT是通过节点域维持平衡的,红黑树通过红黑节点维持平衡。红黑树中序遍历单调不减。

第一棵树:違反中序遍歷不減。
第三课:根节点是黑色。
第四课:红节点子节点是黑色。
第五棵:黑高不相等。
红黑树的遍历简单:小于就走左边,大于就走右边,。
遍历分为广度优先和深度优先。
红黑树从根到叶子节点的最长路径不会超过最短路径的2倍。就保证了自平衡性,不会造成节点全在一个路径上导致变成链表而使得查找效率低。
map.put(12, 12);
map.put(1, 1);
map.put(9, 9);
map.put(2, 2);
map.put(0, 0);
map.put(11, 11);
map.put(7, 7);
map.put(19, 19);
map.put(4, 4);
map.put(15, 15);

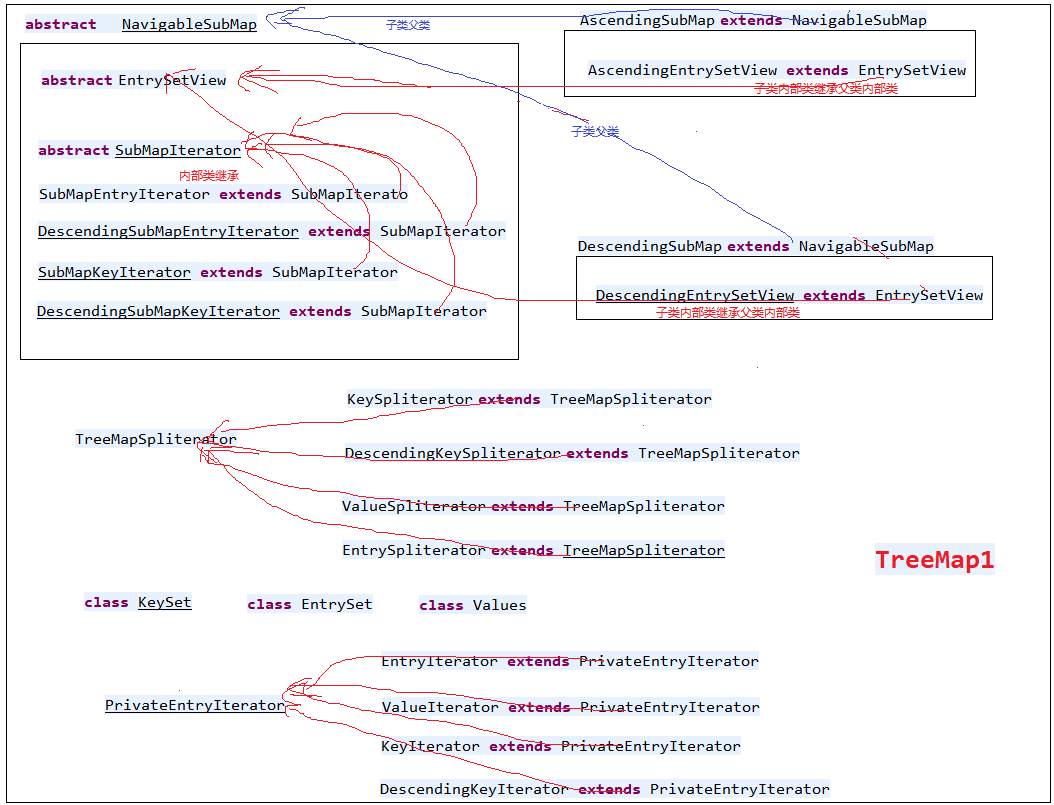
TreeMap的接口: