介绍
接上篇,【搜索引擎(五)】局部敏感哈希,本篇介绍的也是一个不精确的算法,用来不精确地排除重复元素。
利用布隆过滤器,可以大大降低排重的时间。但是在实际中它的作用有限,还要结合其他的技巧才能达到较好的效果。另外,它本身不作为索引,如果不加处理地加以使用,在搜索引擎的快响应(小于1s)的目标中就不能扮演什么重要的角色。
跟LSH一样,它其实也是线性地压缩了比较时间。以网页url去重为例,一个url可能达到上百byte, 字符串一一比较可是很要命的。所以在url去重中,将url进行哈希就可以达到想要的效果。如果以32bit为压缩的最后结果,只考虑非线性查找,压缩时间倍数达到了 25。
原理
布隆过滤器的原理很简单:
当一个元素被加入集合时,通过K个Hash函数将这个元素映射成一个位阵列(Bitarray)中的K个点,把它们置为1。检索时,我们只要看看这些点是不是都是1就(大约)知道集合中有没有它了:
如果这些点有任何一个0,则被检索元素一定不在;
如果都是1,则被检索元素很可能在。
误差率分析:
初始状态时,Bloom Filter是一个包含m位的bit数组,每一位都为0。
有k个不同的哈希函数,每个哈希函数会将集合中的n个元素映射到m个位中。
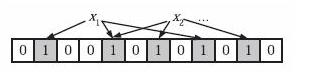
k个哈希函数的要求是两两各自独立。
误差率定义:
对元素(x1, x2, x3 … xn)进行k次映射,结果bit数组中的某一位原来是0, 结果还是为0的概率(说明没有被选中)为:
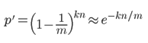
令r为数组中0的比例,则r的数学期望E(r) = p', 在r已知的情况下,所求的误差率(误判为真)为:
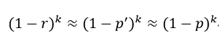
因为1-r为1的期望比例, (1-r)^k表示某一位连续k次哈希为1的概率。
误差率为 f = (1 – p)^k。
为什么是false positive rate?k次哈希都选中了为1的区域,代表错误元素被判为真。由于在现实中假元素在全集中的比例远大于真元素,所以可以用这个来近似表示误差率。
误判率最低的要求:
现在计算对于给定的m和n,k为何值时可以使得误判率最低。设误判率为k的函数为:
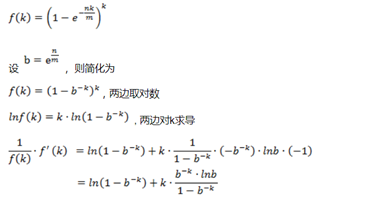

即k在等于ln2* m / n的时候误差率最小,最小误差为:
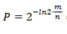
布隆过滤器的参数确定:
给定要加入的元素数n和误差率P, 求需要的每个元素的内存大小:
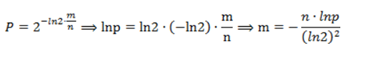
再由m,n得到hash函数的个数:

对应误差查询:
|
比率(items:bits) |
误差率 |
|
1∶1 |
0.63212055882856 |
|
1∶2 |
0.39957640089373 |
|
1∶4 |
0.14689159766038 |
|
1∶8 |
0.02157714146322 |
|
1∶16 |
0.00046557303372 |
|
1∶32 |
0.00000021167340 |
|
1∶64 |
0.00000000000004 |
应用
前面说了一下Bloom Filter的作用不大,但是这是指没有专门处理的Bloom Filter。 结合实际应用场景,平衡好内存的话, Bloom Filter在一些存储和服务系统中也有应用广泛[3]。
Google 著名的分布式数据库 Bigtable 使用了布隆过滤器来查找不存在的行或列,以减少磁盘查找的IO次数。
Squid 网页代理缓存服务器在 cache digests 中使用了也布隆过滤器。
Venti 文档存储系统也采用布隆过滤器来检测先前存储的数据。
SPIN 模型检测器也使用布隆过滤器在大规模验证问题时跟踪可达状态空间。
Google Chrome浏览器使用了布隆过滤器加速安全浏览服务。
在很多Key-Value系统中也使用了布隆过滤器来加快查询过程,如 Hbase,Accumulo,Leveldb,一般而言,Value 保存在磁盘中,访问磁盘需要花费大量时间,然而使用布隆过滤器可以快速判断某个Key对应的Value是否存在,因此可以避免很多不必要的磁盘IO操作,只是引入布隆过滤器会带来一定的内存消耗。
参考
[1] https://www.kancloud.cn/kancloud/the-art-of-programming/41619 (没有给出最优推导)
[2] http://www.cnblogs.com/allensun/archive/2011/02/16/1956532.html (没有给出图例)
[3] http://www.cnblogs.com/haippy/archive/2012/07/13/2590351.html