机器学习--线性回归&贝叶斯算法&KNN&KMeans原理

上篇博客已经初步提到一点线性回归Linner和KNN的，本篇继续对机器学习进行深化！！！

• Python配置 ：Py4j模块、Pyspark模块

• Windows 环境变量：Eclipse开发Pyspark

一. 线性回归

1.什么是回归？

从大量的函数结果和自变量反推回函数表达式的过程就是回归。线性回归是利用数理统计中回归分析来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法。

• 一元线性回归：

只包括一个自变量（x）和一个因变量（y），且二者的关系可用一条直线近似表示，这种回归分析称为一元线性回归分析。公式： y = w₀+w₁x₁

• 多元线性回归：

如果回归分析中包括两个或两个以上的自变量，且因变量和自变量之间是线性关系，则称为多元线性回归分析。公式：Ε(w0+w1x1+...+ w_nx_n)

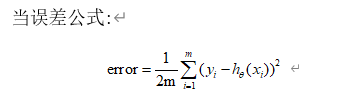
代表一系列的真实离散点的y值，

代表一系列得到的直线在对应的x处的y值，一元线性回归中=。

m代表有m个离散点，前面的 是为了方便求导加上的。

 表示的是一系列权重,,…. 

这个公式也叫做最小二乘法误差公式。error的值如果是0说明确定的这条直线穿过了所有的点，对于离散分散的一组点，error的值不可能为0。

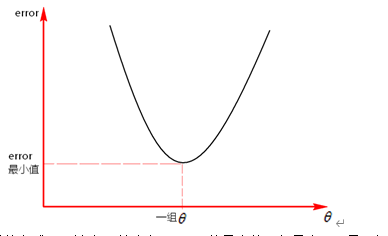
通过求导的方式，理论上可以确定error的最小值，但是由于是一组数据，无法确定error最小下对应的这一组权重 。

正向的求导不能得到一组权重值，就不能确定线性回归的公式。那么可以根据数据集来穷举法反向的试，来确定线性回归的公式：

 

 

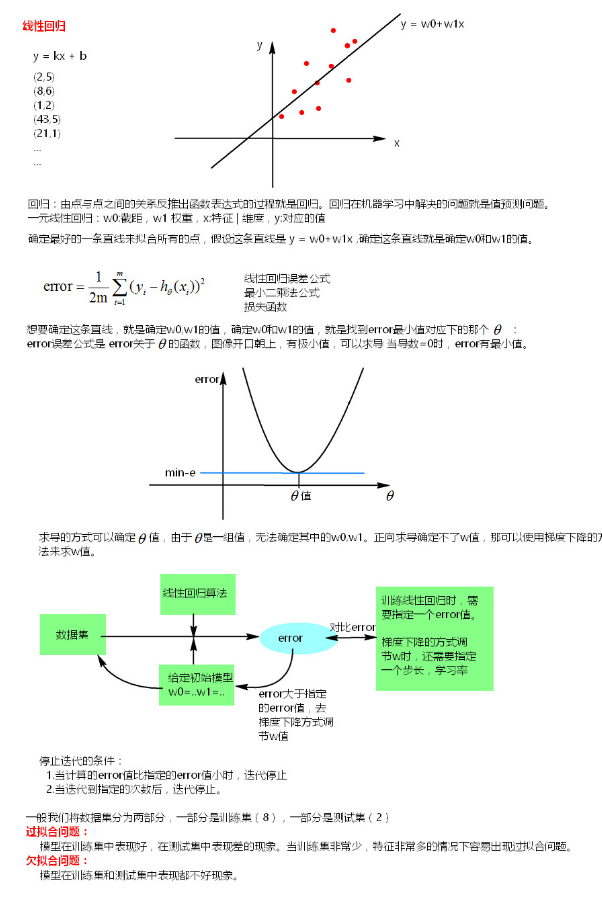
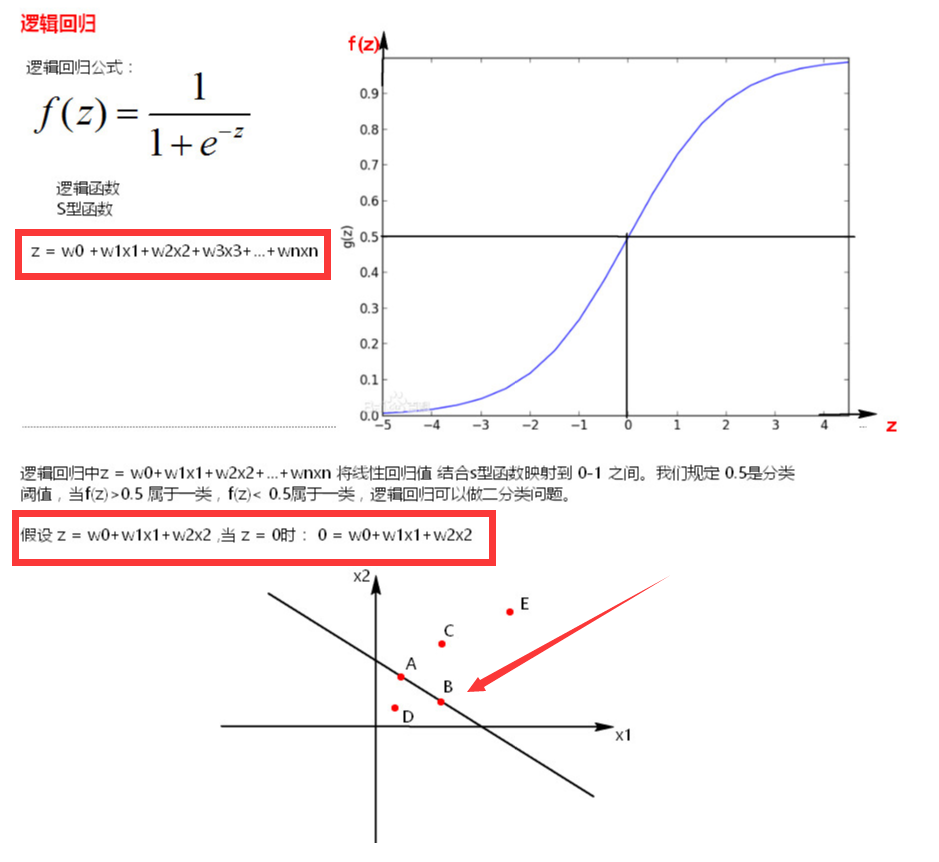
2. 梯度下降法调节参数

假设和error的函数关系中，中只有一个维度，那么这个关系其实就是和error的关系，反应图上就是一维平面关系，如果中有两个维度和，那么这个反映到图上就是个三维空间关系，以此类推。

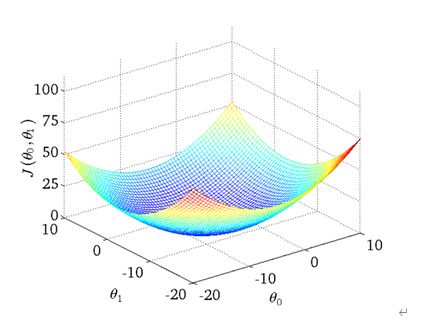
如果中只有一个维度，如下图：

 

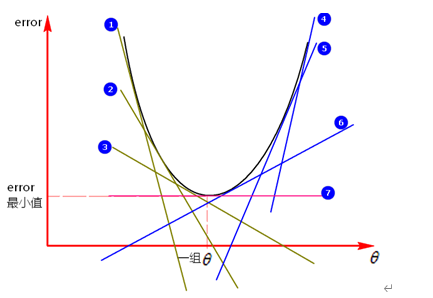
图中①，②，③，④，⑤，⑥，⑦都是图像的切线（斜率），在切点处可以求得对应的error值，如何调节模型得到一组 值可以使得到的error值更小，如图，沿着①->②->③方向调节和沿着④->⑤->⑥方向调节，可以使error值更小，这种沿着斜率绝对值减少的方向,沿着梯度的负方向每次迭代调节的方法就叫做梯度下降法。

梯度下降是迭代法的一种,可以用于求解最小二乘问题，在求解error函数的最小值时，可以通过梯度下降法来一步步的迭代求解，得到最小化的error函数和模型参数值。

每次按照步长(学习率)来调节值，迭代求出error的最小值，这里的error不可能有一个固定的最小值，只会向着最小值的方向收敛。

判断模型error误差值收敛，也就是停止迭代的两种方式：

• • 指定一个error值，当迭代处理过程中得到的error值小于指定的值时，停止迭代。
  • 设置迭代次数，当迭代次数达到设置的次数时，停止迭代。

迭代周期：从调整参数开始到计算出error值判断是否大于用户指定的error是一个迭代周期。

当步长比较小时，迭代次数多，训练模型的时间比较长，当步长比较大时，有可能迭代的次数也比较多，训练模型的时间也会相对比较长，需要找到一个合适的步长。 

3. 模型过拟合

训练模型都会将数据集分为两部分，一般会将0.8比例的数据集作为训练集，将0.2比例的数据集作为测试集，来训练模型。模型过拟合就是训练出来的模型在训练集上表现很好，但是在测试集上表现较差的一种现象，也就是模型对已有的训练集数据拟合的非常好（误差值等于0），对于测试集数据拟合的非常差，模型的泛化能力比较差。

4.如何判断模型发生过拟合？

训练出模型后，可以在训练集中测试下模型的正确率，在测试集中测试下模型的正确率，如果两者差别很大（测试集正确率小，训练集正确率大），那么模型就有可能发生了过拟合。

5.Spark Mllib 线性回归案例

object LinearRegression {

  def main(args: Array[String]) {
    // 构建Spark对象
    val conf = new SparkConf().setAppName("LinearRegressionWithSGD").setMaster("local")
    val sc = new SparkContext(conf)
    Logger.getRootLogger.setLevel(Level.WARN)
//        sc.setLogLevel("WARN")

    //读取样本数据
    val data_path1 = "lpsa.data"
    val data = sc.textFile(data_path1)
    val examples = data.map { line =>
      val parts = line.split(',')
      val y = parts(0)
      val xs = parts(1)
      LabeledPoint(parts(0).toDouble, Vectors.dense(parts(1).split(' ').map(_.toDouble)))
    }.cache()

    val train2TestData = examples.randomSplit(Array(0.8, 0.2), 1)

    /*
     *  迭代次数
     *  训练一个多元线性回归模型收敛（停止迭代）条件：
     *      1、error值小于用户指定的error值
     *      2、达到一定的迭代次数
     */
    val numIterations = 100

    //在每次迭代的过程中 梯度下降算法的下降步长大小    0.1 0.2 0.3 0.4
    val stepSize = 1

    
    val miniBatchFraction = 1
    val lrs = new LinearRegressionWithSGD()
    //让训练出来的模型有w0参数，就是由截距
    lrs.setIntercept(true)
    //设置步长
    lrs.optimizer.setStepSize(stepSize)
    //设置迭代次数
    lrs.optimizer.setNumIterations(numIterations)
    //每一次下山后，是否计算所有样本的误差值,1代表所有样本,默认就是1.0
    lrs.optimizer.setMiniBatchFraction(miniBatchFraction)

    val model = lrs.run(train2TestData(0))
    println(model.weights)
    println(model.intercept)

    // 对样本进行测试
    val prediction = model.predict(train2TestData(1).map(_.features))
    val predictionAndLabel = prediction.zip(train2TestData(1).map(_.label))
    
    val print_predict = predictionAndLabel.take(20)
    println("prediction" + "	" + "label")
    for (i <- 0 to print_predict.length - 1) {
      println(print_predict(i)._1 + "	" + print_predict(i)._2)
    }
    
    // 计算测试集平均误差
    val loss = predictionAndLabel.map {
      case (p, v) =>
        val err = p - v
        Math.abs(err)
    }.reduce(_ + _)
    val error = loss / train2TestData(1).count
    println(s"Test RMSE = " + error)
    // 模型保存
    val ModelPath = "model"
    model.save(sc, ModelPath)
//    val sameModel = LinearRegressionModel.load(sc, ModelPath)
    sc.stop()
  }

二.贝叶斯分类算法

1.朴素贝叶斯

朴素贝叶斯（Naive Bayes ,NB）算法是基于贝叶斯定理与特征条件独立假设的分类方法，该算法是有监督的学习算法，解决的是分类问题，是将一个未知样本分到几个预先已知类别的过程。

朴素贝叶斯的思想就是根据某些个先验概率计算Y变量属于某个类别的后验概率，也就是根据先前事件的有关数据估计未来某个事件发生的概率。

2.拉普拉斯估计

拉普拉斯估计本质上是给频率表中的每个单词的计数加上一个较小的数，这样就保证每一类中每个特征发生的概率非零。通常，拉普拉斯估计中加上的数值为1，这样就保证了每一个特征至少在数据中出现一次。

3.Python实现

import os
import sysecs 编码转换模块
import codecs
from sklearn.naive_bayes import MultinomialNB  
from sklearn.feature_extraction.text import CountVectorizer

if __name__ == '__main__':
    # 读取文本构建语料库
    corpus = []
    labels = []
    corpus_test = []
    labels_test = []
    f = codecs.open("i:/ML/sms_spam.txt", "rb")  
    count = 0
    while True:  
        line = f.readline()  
        if count == 0:
            count = count + 1
            continue
        if line:  
            count = count + 1
            line = line.split(",")
            label = line[0]
            sentence = line[1]
            corpus.append(sentence)
            if "ham"==label:
                labels.append(0)
            elif "spam"==label:
                labels.append(1)
            if count > 5550:
                corpus_test.append(sentence)
                if "ham"==label:
                    labels_test.append(0)
                elif "spam"==label:
                    labels_test.append(1)
        else:
            break
    #CountVectorizer是将文本向量转换成稀疏表示数值向量（字符频率向量）  vectorizer 将文档词块化
    vectorizer=CountVectorizer()
    fea_train = vectorizer.fit_transform(corpus)
    print vectorizer.get_feature_names()
print fea_train.toarray()

    vectorizer2=CountVectorizer(vocabulary=vectorizer.vocabulary_)
    fea_test = vectorizer2.fit_transform(corpus_test)
rint vectorizer2.get_feature_names()
    print fea_test.toarray()
    #create the Multinomial Naive Bayesian Classifier 
    #alpha = 1 拉普拉斯估计给每个单词加1 
    clf = MultinomialNB(alpha = 1)   
    clf.fit(fea_train,labels)
#    
    pred = clf.predict(fea_test);  
    for p in pred:
        if p == 0:
            print "正常邮件"
        else:
            print "垃圾邮件"

 4.cala 贝叶斯案例

object Naive_bayes {
  def main(args: Array[String]) {
    //1 构建Spark对象
    val conf = new SparkConf().setAppName("Naive_bayes").setMaster("local")
    val sc = new SparkContext(conf)
    //读取样本数据1
    val data = sc.textFile("sample_naive_bayes_data.txt")
    val parsedData = data.map { line =>
      val parts = line.split(',')
      LabeledPoint(parts(0).toDouble, Vectors.dense(parts(1).split(' 、').map(_.toDouble)))
    }

    //样本数据划分训练样本与测试样本
    val splits = parsedData.randomSplit(Array(0.9, 0.1), seed = 11L)
    val training = splits(0)
    val test = splits(1)

    //新建贝叶斯分类模型模型，并训练 ,lambda 拉普拉斯估计
    val model = NaiveBayes.train(training, lambda = 1.0)

    //对测试样本进行测试
    val predictionAndLabel = test.map(p => (model.predict(p.features), p.label))
    val print_predict = predictionAndLabel.take(10020)
    println("prediction" + "	" + "label")
    for (i <- 0 to print_predict.length - 1) {
      println(print_predict(i)._1 + "	" + print_predict(i)._2)
    }
    
val accuracy = 1.0 * predictionAndLabel
.filter(x => x._1 == x._2).count() / test.count()
    println(accuracy)
    //保存模型
    val ModelPath = "naive_bayes_model"
    model.save(sc, ModelPath)
    val sameModel = NaiveBayesModel.load(sc, ModelPath)
  }
}

 

三.KNN最邻近算法

K最近邻(k-Nearest Neighbor，KNN)分类算法，是一个理论上比较成熟的方法，也是最简单的机器学习算法之一，有监督算法。该方法的思路是：如果一个样本在特征空间中的k个最相似的样本中的大多数属于某一个类别，则该样本也属于这个类别。KNN算法由你的邻居来推断出你的类别，KNN算法就是用距离来衡量样本之间的相似度。

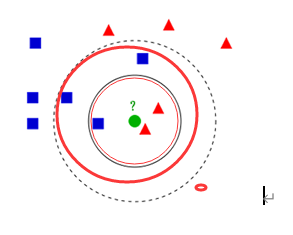
如果K = 3，绿色圆点的最近的3个邻居是2个红色小三角形和1个蓝色小正方形，少数从属于多数，基于统计的方法，判定绿色的这个待分类点属于红色的三角形一类。

如果K = 5，绿色圆点的最近的5个邻居是2个红色三角形和3个蓝色的正方形，还是少数从属于多数，基于统计的方法，判定绿色的这个待分类点属于蓝色的正方形一类。

K 值的选择，距离度量和分类决策规则是该算法的三个基本要素。K值的选择一般低于样本数据的平方根,一般是不大于20的整数。距离度量常用的有欧式距离，曼哈顿距离，余弦距离等，一般使用欧氏距离，对于文本分类，常用余弦距离。分类决策就是“少数服从多数”的策略。 

1.KNN算法步骤：

1)  对于未知类别的数据（对象，点），计算已知类别数据集中的点到该点的距离。

2)  按照距离由小到大排序

3)  选取与当前点距离最小的K个点

4)  确定前K个点所在类别出现的概率

5)  返回当前K个点出现频率最高的类别作为当前点预测分类

2.KNN算法复杂度：

KNN 分类的计算复杂度和训练集中的文档数目成正比，也就是说，如果训练集中文档总数为 n，那么 KNN 的分类时间复杂度为O(n)

3.KNN问题：

该算法在分类时有个主要的不足是，当样本不平衡时，如一个类的样本容量很大，而其他类样本容量很小时，有可能导致当输入一个新样本时，该样本的 K 个邻居中大容量类的样本占多数。解决：可以采用权值的方法，根据和该样本距离的远近，对近邻进行加权，距离越小的邻居权值大，权重一般为距离平方的倒数。

4.KNN数据归一化：

为了防止某一维度的数据的数值大小对距离计算产生影响，保证多个维度的特征是等权重的，最终结果不能被数值的大小影响，应该将各个维度进行数据的归一化，把数据归一化到[0,1]区间上。

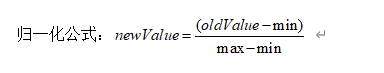
5.距离度量

• 欧式距离：也称欧几里得距离，在一个N维度的空间里，求两个点的距离，这个距离肯定是一个大于等于零的数字，那么这个距离需要用两个点在各自维度上的坐标相减，平方后加和再开方。一维，二维，三维的欧式距离计算方法：一维：  二维：  三维：  

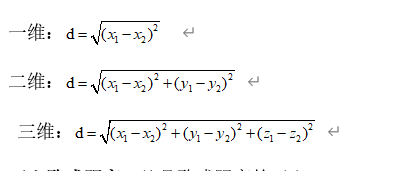
• 平方欧式距离：就是欧式距离的平方。
• 曼哈顿距离：相比欧式距离简单的多，曼哈顿距离只要把两个点坐标的x坐标相减取绝对值，y坐标相减取绝对值，再加和，

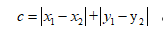
  。三维，四维以此类推。

•  余弦距离：也叫余弦相似度，是用向量空间中两个向量夹角的余弦值作为衡量两个个体间差异的大小的度量。如果两个向量的方向一致，即夹角接近零，那么这两个向量就越相近。要确定两个向量方向是否一致，要用到余弦定理计算向量的夹角。
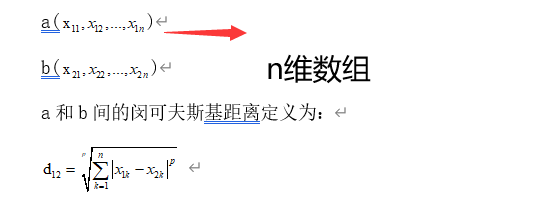
• 闵可夫斯基距离：闵式距离不是一种距离，而是一组距离的定义，是对多个距离度量公式的概括性表述。定义：两个n维变量（可以理解为n维数组，就是有n个元素）a()与b()间的闵可夫斯基距离定义为： 其中p是一个变参数，当p=1时，就是曼哈顿距离，当p=2时，就是欧式距离，当p 就是切比雪夫距离。

• 切比雪夫距离：国际象棋中，国王可以直行、横行、斜行。国王走一步，可以移动到相邻的8个方格的任意一个。国王从格子 到格子最少需要多少步？这个距离就是切比雪夫距离。
• 谷本距离：同时考虑余弦距离和欧式距离的测度。
• 加权距离测度：可以指定某一维度的权重比例，从而使某个权重的影响力更大。

6.KNN案例

import numpy as np
import operator
#matplotata 测试数据集的某行，  dataSet 训练数据集 ，labels 训练数据集的类别，k k的值
def classify(normData,dataSet,labels,k):
    dataSetSize = dataSet.shape[0]
#     print 'dataSetSize 长度 =',dataSetSize
    #当前点到所有点的坐标差值
    diffMat = np.tile(normData, (dataSetSize,1)) - dataSet
    #对每个坐标差值平方
    sqDiffMat = diffMat ** 2
    #对于二维数组 sqDiffMat.sum(axis=0)指定对数组b对每列求和，sqDiffMat.sum(axis=1)是对每行求和
    sqDistances = sqDiffMat.sum(axis = 1)
    #欧式距离 最后开方
    distance = sqDistances ** 0.5
    #argsort() 将x中的元素从小到大排序，提取其对应的index 索引，返回数组
    sortedDistIndicies = distance.argsort()
#     classCount保存的K是魅力类型   V:在K个近邻中某一个类型的次数
    classCount = {}
    for i in range(k):
        #获取对应的下标的类别
        voteLabel = labels[sortedDistIndicies[i]]
        #给相同的类别次数计数
        classCount[voteLabel] = classCount.get(voteLabel,0) + 1
    sortedClassCount = sorted(classCount.iteritems(),key=operator.itemgetter(1),reverse=True)
    return sortedClassCount[0][0]

def file2matrix(filename):
    fr = open(filename)
#     readlines:是一次性将这个文本的内容全部加载到内存中(列表)
    arrayOflines = fr.readlines()
    numOfLines = len(arrayOflines)
#     print "numOfLines = " , numOfLines
    #numpy.zeros 创建给定类型的矩阵  numOfLines 行 ，3列
    returnMat = np.zeros((numOfLines,3))
    classLabelVector = []
    index = 0
    for line in arrayOflines:
        #去掉一行的头尾空格
        line = line.strip()
        listFromline = line.split('	')
        returnMat[index,:] = listFromline[0:3]
        classLabelVector.append(int(listFromline[-1]))
        index += 1
    return returnMat,classLabelVector
'''
    将训练集中的数据进行归一化
    归一化的目的：
        训练集中飞行公里数这一维度中的值是非常大，那么这个纬度值对于最终的计算结果(两点的距离)影响是非常大，
        远远超过其他的两个维度对于最终结果的影响
    实际约会姑娘认为这三个特征是同等重要的
    下面使用最大最小值归一化的方式将训练集中的数据进行归一化
'''
#将数据归一化
def autoNorm(dataSet):
#     dataSet.min(0)   代表的是统计这个矩阵中每一列的最小值     返回值是一个矩阵1*3矩阵
    minVals = dataSet.min(0)
    maxVals = dataSet.max(0)
    ranges = maxVals - minVals
    #dataSet.shape[0] 计算行数， shape[1] 计算列数
    m = dataSet.shape[0]
#     normDataSet存储归一化后的数据
#     normDataSet = np.zeros(np.shape(dataSet))
    #np.tile(minVals,(m,1)) 在行的方向上重复 minVals m次 即复制m行，在列的方向上重复munVals 1次，即复制1列
    normDataSet = dataSet - np.tile(minVals,(m,1))
    normDataSet = normDataSet / np.tile(ranges,(m,1))
    return normDataSet,ranges,minVals
def datingClassTest():
    hoRatio = 0.1
    datingDataMat,datingLabels = file2matrix('datingTestSet2.txt')
    #将数据归一化
    normMat,ranges,minVals = autoNorm(datingDataMat)
    # m 为行数 = 1000
    m = normMat.shape[0]
#     print 'm =%d 行'%m
    #取出100行数据测试
    numTestVecs = int(m*hoRatio)
    errorCount = 0.0
    for i in range(numTestVecs):
        #normMat[i,:] 取出数据的第i行,normMat[numTestVecs:m,:]取出数据中的100行到1000行 作为训练集，datingLabels[numTestVecs:m] 取出数据中100行到1000行的类别，4是K
        classifierResult = classify(normMat[i,:],normMat[numTestVecs:m,:],datingLabels[numTestVecs:m],4)
        print '模型预测值: %d ,真实值 : %d' %(classifierResult,datingLabels[i])
        if (classifierResult != datingLabels[i]):
            errorCount += 1.0
    errorRate = errorCount / float(numTestVecs)
    print '正确率 : %f' %(1-errorRate)
    return 1-errorRate

def classifyperson():
    resultList = ['没感觉', '看起来还行','极具魅力']
    input_man= [30000,3,0.1]
    datingDataMat,datingLabels = file2matrix('datingTestSet2.txt')
    normMat,ranges,minVals = autoNorm(datingDataMat) 
    result = classify((input_man - minVals)/ranges,normMat,datingLabels,3)   
    print '你即将约会的人是:' ,  resultList[result-1]                             
if __name__ == '__main__':
    acc = datingClassTest()
    if(acc > 0.9):
        classifyperson()

四.K-means聚类算法

 机器学习中有两类的大问题，一个是分类，一个是聚类。分类是监督学习，原始数据有标签，可以根据原始数据建立模型，确定新来的数据属于哪一类。聚类是一种无监督学习，聚类是指事先没有“标签”，在数据中发现数据对象之间的关系，将数据进行分组，一个分组也叫做“一个簇”， 组内的相似性越大，组间的差别越大，则聚类效果越好，也就是簇内对象有较高的相似度，簇之间的对象相似度比较低，则聚类效果越好。K-means就是一个聚类算法。

 

K-means算法的思想就是对空间K个点为中心进行聚类，对靠近他们的对象进行归类，通过迭代的方法，逐次更新聚类中心(质心)的值，直到得到最好的聚类结果。K-means过程：

• • 1. 首先选择k个类别的中心点
  • 2. 对任意一个样本，求其到各类中心的距离，将该样本归到距离最短的中心所在的类
  • 3. 聚好类后，重新计算每个聚类的中心点位置
  • 4. 重复2,3步骤迭代，直到k个类中心点的位置不变，或者达到一定的迭代次数，则迭代结束，否则继续迭代

1. K-means++算法

K-means算法假设聚类为3类，开始选取每个类的中心点的时候是随机选取，有可能三个点选取的位置非常近，导致后面每次聚类重新求各类中心的迭代次数增加。K-means++在选取第一个聚类中心点的时候也是随机选取，当选取第二个中心点的时候，距离当前已经选择的聚类中心点的距离越远的点会有更高的概率被选中，假设已经选取n个点，当选取第n+1个聚类中心时，距离当前n个聚类中心点越远的点越会被选中，这种思想是聚类中心的点离的越远越好，这样就大大降低的找到最终聚类各个中心点的迭代次数，提高了效率。

2.K-means找中心点和数据点分类例子

import numpy as np将每行数据放入一个数组内列表，返回一个二维列表
def loadDataSet(fileName):  建空列表     
    dataMat = []                 
    fr = open(fileName)
    for line in fr.readlines():
        #按照制表符切割每行，返回一个列表list
        curLine = line.strip().split('	')切分后的每个列表中的元素，以float形式返回，map()内置函数，返回一个list
        fltLine = map(float,curLine) 
        dataMat.append(fltLine)
    return dataMat
离
def distEclud(vecA, vecB):
    return np.sqrt(np.sum(np.power(vecA - vecB, 2)))
3个中心点的位置坐标，返回一个3*2的矩阵
def randCent(dataSet, k):列数,2列
    n = np.shape(dataSet)[1]
    '''
        centroids是一个3*2的矩阵，用于存储三个中心点的坐标
    '''
    centroids = np.mat(np.zeros((k,n))) 
    for j in range(n): 
        #统计每一列的最小值
        minJ = min(dataSet[:,j]) 
        #每列最大值与最小值的差值
        rangeJ = float(max(dataSet[:,j]) - minJ)
        #random.rand(k,1) 产生k*1的数组，里面的数据是0~1的浮点型。
        array2 = minJ + rangeJ * np.random.rand(k,1)
        #转换成k*1矩阵 赋值给centroids
        centroids[:,j] = np.mat(array2)
    return centroids

def kMeans(dataSet, k, distMeas=distEclud, createCent=randCent):
    #计算矩阵所有行数  80
    m = np.shape(dataSet)[0]
y.mat 将二维数组转换成矩阵
    clusterAssment = np.mat(np.zeros((m,2)))
createCent找到K个随机中心点坐标
    centroids = createCent(dataSet, k)
#     print centroids
    clusterChanged = True
    while clusterChanged:
        clusterChanged = False
        #遍历80个数据到每个中心点的距离
        for i in range(m): 
            #np.inf float的最大值，无穷大
            minDist = np.inf
            #当前点属于的类别号
            minIndex = -1
            #每个样本点到三个中心点的距离
            for j in range(k):
返回两点距离的值
                distJI = distMeas(centroids[j,:],dataSet[i,:])
                if distJI < minDist:
                    #当前最小距离的值
                    minDist = distJI
                    #当前最小值属于哪个聚类
                    minIndex = j
            #有与上次迭代计算的当前点的类别不相同的点
            if clusterAssment[i,0] != minIndex: 
                clusterChanged = True
            #将当前点的类别号和最小距离 赋值给clusterAssment的一行
            clusterAssment[i,:] = minIndex,minDist
        for cent in range(k): 
ent[:,0].A==censInClust 取出的是对应是当前遍历cent类别的 所有行数据组成的一个矩阵
            ptsInClust = dataSet[np.nonzero(clusterAssment[:,0].A==cent)[0]]心点坐标的位置
            centroids[cent,:] = np.mean(ptsInClust, axis=0)  
    #返回 【 当前三个中心点的坐标】 【每个点的类别号，和到当前中心点的最小距离】
    return centroids, clusterAssment

if __name__ == '__main__': 80*2的矩阵
    dataMat = np.mat(loadDataSet('./testSet.txt'))
    k=3
centroids, clusterAssment = 
kMeans(dataMat, k, distMeas=distEclud, createCent=randCent)
    print centroids
    print clusterAssment 

3.使用matplotlib检验分类效果

import numpy as np       
import matplotlib.pyplot as plt       
from sklearn.cluster import KMeans        
from sklearn.datasets import make_blobs  

#建立12*12新的图像
plt.figure(figsize=(12, 12)) 
n_samples = 1500
random_state = 170
'''
    make_blobs函数是为聚类产生数据集 ， 产生一个数据集和相应的标签 
        n_samples:表示数据样本点个数,默认值100 
        n_features:表示数据的维度，特征，默认值是2 
        centers:产生数据的中心点，默认值3个 
        shuffle ：洗乱，默认值是True 
        random_state:官网解释是随机生成器的种子 
'''
#x返回的是向量化的数据点，y返回的是对应数据的类别号
x,y = make_blobs(n_samples=n_samples, random_state=random_state)  
#使用KMeans去聚类,返回聚好的类别集合,聚合成几类
y_pred = KMeans(n_clusters=3, random_state=random_state).fit_predict(x) 

#subplot 绘制多个子图，221 等价于2,2,1 表示两行两列的子图中的第一个
plt.subplot(221)
#scatter 绘制散点图
plt.scatter(x[:, 0], x[:, 1], c=y_pred)    
plt.title("kmeans01") 

  
transformation = [[ 0.60834549, -0.63667341], [-0.40887718, 0.85253229]] 
#numpy.dot 矩阵相乘 
X_aniso = np.dot(x, transformation)     
y_pred = KMeans(n_clusters=3, random_state=random_state).fit_predict(X_aniso)  
plt.subplot(222)
plt.scatter(X_aniso[:, 0], X_aniso[:, 1], c=y_pred)  
plt.title("kmeans02") 

  
#vstack 是合并矩阵，将y=0类别的取出500行，y=1类别的取出100行，y=2类别的取出10行
X_filtered = np.vstack((x[y == 0][:500], x[y == 1][:100], x[y == 2][:10]))  
y_pred = KMeans(n_clusters=3, random_state=random_state).fit_predict(X_filtered)  
plt.subplot(223) 
plt.scatter(X_filtered[:, 0], X_filtered[:, 1], c=y_pred)  
plt.title("kmeans03")


dataMat = []                
fr = open("testSet.txt","r")
for line in fr.readlines():
    if line.strip() <> "":
        curLine = line.strip().split('	')
        fltLine = map(float,curLine)  
        dataMat.append(fltLine)
dataMat = np.array(dataMat)
y_pred = KMeans(n_clusters=4, random_state=random_state).fit_predict(dataMat) 
plt.subplot(224) 
plt.scatter(dataMat[:,0], dataMat[:, 1], c=y_pred)  
plt.title("kmeans04") 
plt.savefig("./kmeans.png")
plt.show() 

4.使用SparkMllib训练K-means模型

object KMeans {

  def main(args: Array[String]) {
    //1 构建Spark对象
    val conf = new SparkConf().setAppName("KMeans").setMaster("local")
    val sc = new SparkContext(conf)

    // 读取样本数据1，格式为LIBSVM format
    val data = sc.textFile("kmeans_data.txt")
val parsedData = data.map(s => Vectors.dense(s.split(' ')
.map(_.toDouble))).cache()
    val numClusters = 4
    val numIterations = 100
    val model = new KMeans().
      //设置聚类的类数
      setK(numClusters).
      //设置找中心点最大的迭代次数
      setMaxIterations(numIterations).
      run(parsedData)
      
    //四个中心点的坐标
    val centers = model.clusterCenters
    val k = model.k
    centers.foreach(println)
    println(k)
    //保存模型
//    model.save(sc, "./Kmeans_model")
    //加载模型
    val sameModel = KMeansModel.load(sc, "./Kmeans_model")
    println(sameModel.predict(Vectors.dense(1,1,1)))
    val sqlContext = new SQLContext(sc)
    sqlContext.read.parquet("./Kmeans_model/data").show()
    
  }
}

给Kmeans指定中心点坐标：

object KMeans2 {

  def main(args: Array[String]) {
    val conf = new SparkConf().setAppName("KMeans2").setMaster("local")
    val sc = new SparkContext(conf)

    val rdd = sc.parallelize(List(
      Vectors.dense(Array(-0.1, 0.0, 0.0)),
      Vectors.dense(Array(9.0, 9.0, 9.0)),
      Vectors.dense(Array(3.0, 2.0, 1.0))))
      
    //指定文件 kmeans_data.txt 中的六个点为中心点坐标。
    val centroids: Array[Vector] = sc.textFile("kmeans_data.txt")
        .map(_.split(" ").map(_.toDouble))
        .map(Vectors.dense(_))
        .collect()
    val model = new KMeansModel(clusterCenters=centroids)
    println("聚类个数 = "+model.k)
    //模型中心点
    model.clusterCenters.foreach { println }
    //预测指定的三条数据
    val result = model.predict(rdd)
    result.collect().foreach(println(_))
  }
}

---------总结------------