拓端tecdat|R语言圆填充( Circle packing)算法圆堆图圆形空间填充算法可视化

原文链接：http://tecdat.cn/?p=24658 

原文出处：拓端数据部落公众号

圆填充Circle packing算法

已经开发了大量确定性和随机性的圆填充算法。

• RepelLayout 通过成对排斥迭代移动圆圈来搜索非重叠布局。圆的位置被限制在一个矩形区域内。为避免边缘效应，可以将边界区域视为环面，例如，推到左侧边缘的圆将重新进入右侧边缘的边界区域。这是一种非常简单且效率相当低的算法，但通常会产生良好的结果。

• ProgressiveLayout 连续放置圆，使每个圆与先前放置的两个圆在外部相切。该算法是确定性的，尽管可以通过改变输入圆圈的顺序产生不同的布局。它非常高效，因此适用于处理大型数据集。 

• GraphLayout 试图找到满足输入邻接图的安排。实现是实验性的。 

第一个例子

我们将首先创建一组不同大小的圆，然后找到可以用 ggplot 显示的非重叠排列。

首先，我们创建一组随机圆，位于边界正方形的中心部分，较小的圆比较大的圆更常见。我们将圆的大小表示为面积。 

1.  
    
2.  
   as <- reta(rcs ,5) * maxaa

接下来，我们尝试找到一个不重叠的排列，允许圆圈占据边界正方形的任何部分。返回值是一个包含布局元素和执行迭代次数的列表。

1.  
    
2.  
   Layout(areass)
3.  
    

布局作为具有圆心坐标和半径的数据框返回。

head( layout )

我们将其转换为圆形顶点的数据集，用 ggplot 显示。

结果数据集有一个整数 id 字段，它对应于传递给 的原始数据中圆圈的位置。

1.  
    
2.  
   head(dtg)

现在我们可以绘制布局了。

1.  
    
2.  
   themebw()
3.  
    
4.  
   thest(t)
5.  
   ggplot(daa = d.g)

 基于图的圆填充

圆填充的另一种方法是从指定圆的大小和相切（即哪些圆接触哪些其他圆）开始，然后搜索满足此要求的排列。

在下图中，左侧的图形表示所需的圆相切模式。圆 5、7、8 和 9 是 内部的，而其余​​圆圈是 外部的。右边的圆填充显示了符合输入图的圆圈排列。

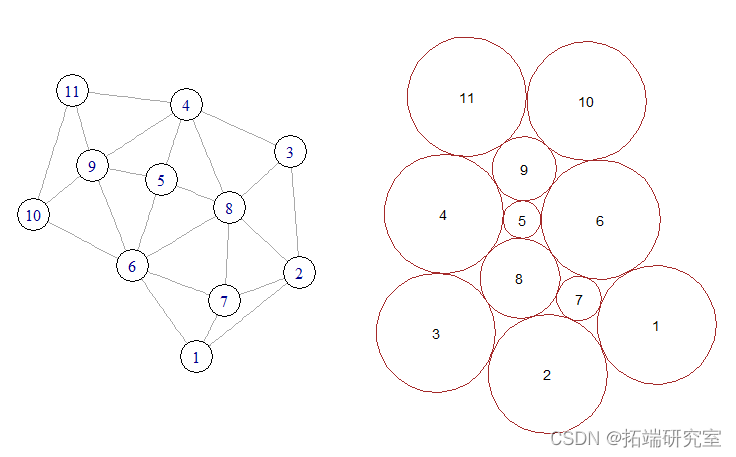
切线图和结果堆积

GraphLayout 实现了算法的基本版本。下面的例子产生一个类似于上图的布局：

1.  
    
2.  
    
3.  
   ## 切线列表。矢量元素是圆 ID。
4.  
   ##每个向量的第一个元素是一个内圆
5.  
   ## 和随后的元素是它的邻居。
6.  
    
7.  
    
8.  
   ## 外圆半径。
9.  
   data.frame(id )
10.  
     
11.  
    ## Layout 函数用于查找排列
12.  
    ##与`internal`指定的切线相对应的圆
13.  
    ## 和由 `external` 指定的外圆尺寸。结果是一个四列的 data.frame: id, x, y, radi。
14.  
    ##
15.  
    circleGraphLayout
16.  
     
17.  
    ## 获取圆顶点的数据
18.  
    LayotVtics(laout,xyizcs = 2:4, dl = 1)
19.  
    ## 绘制带有 ID 注释的圆圈。
20.  
    ggplot() +
21.  
    geom_olon(）+
22.  
     
23.  
    ge_tet(data=ayo) +
24.  
     
25.  
    oal()

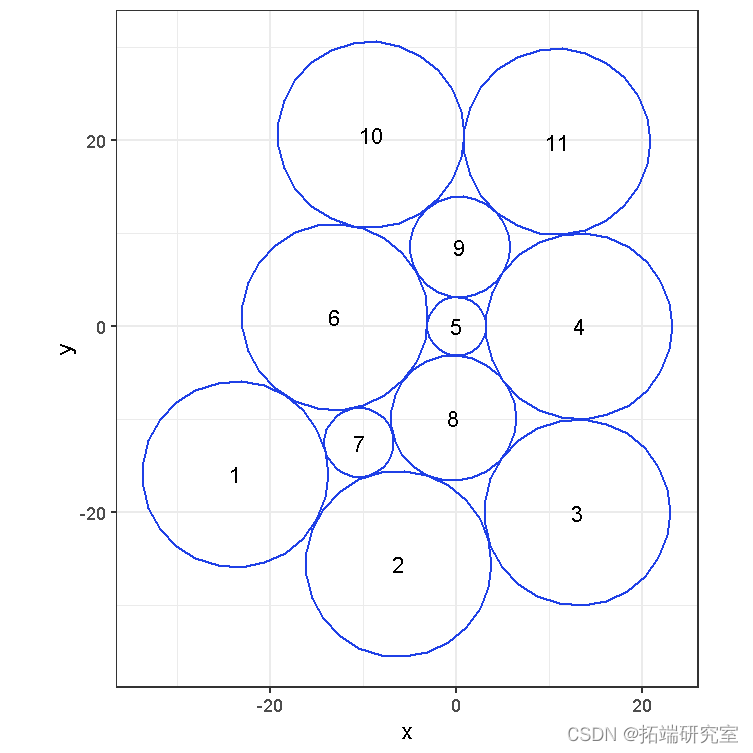
指定初始圆位置

在前面的示例中，我们将圆大小的向量传递给 circleRepelLayout，该函数通过将圆放置在靠近边界区域中心的位置，为圆随机分配起始位置。或者，我们可以预先指定初始位置。为了说明这一点，我们首先将所有圆圈放置在边界区域的一个角附近。

1.  
    
2.  
    
3.  
   lLayout(dt.nt)
4.  
    

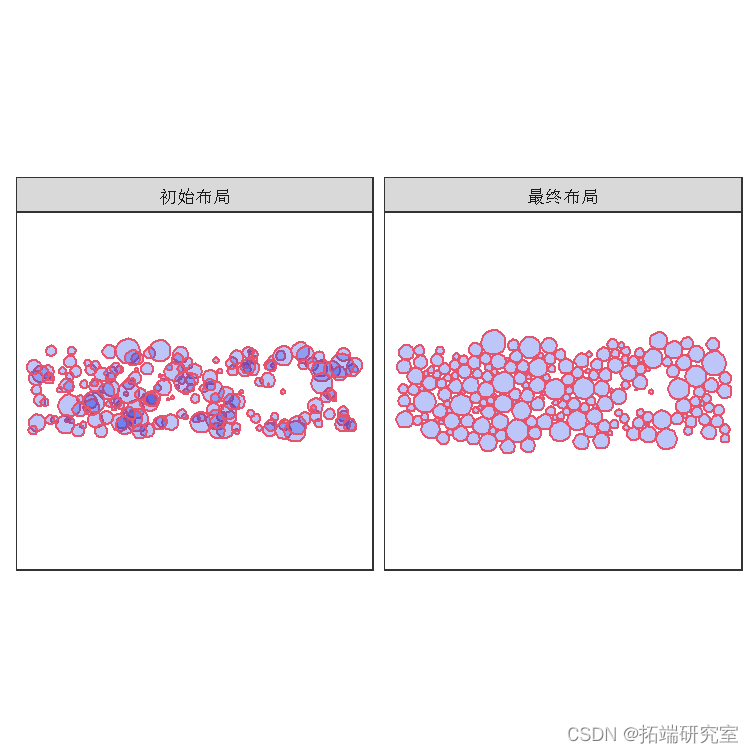
接下来我们使用 ggplot 显示初始和最终布局。请注意，在我们的初始布局中，我们将圆的大小表示为面积，因此我们需要在调用Vertices 函数时指定 ，否则它假定大小是半径。

1.  
    
2.  
   # 获取初始布局的顶点数据，其中大小是区域
3.  
   dgil - ciLocs(dt., sieye = "area")
4.  
   # 获取函数返回的布局的顶点数据 whre
5.  
   # 尺寸是半径
6.  
   a..i <- ciaoees(rlyout)
7.  
    
8.  
    
9.  
   ggplot(data
10.  
    ge_pgon(couaa=0.3) +
11.  
     
12.  
    cor_el(xli=lis yl=imts)

移动和固定

RepelLayout 函数接受一个可选 weights 参数，以在布局算法的每次迭代中对圆的移动进行额外控制。该参数采用一个数值向量，其值在 0-1 范围内（此范围之外的任何值都将被限制为 0 或 1）。权重为 0 可防止圆完全移动，而权重为 1 则允许完全移动。

为了说明这一点，我们将从更早使用的数据集中选择几个圆圈，将它们放大并通过将它们的权重设置为 0.0 来固定它们的位置。

1.  
    
2.  
   # 选择几个任意的圆圈
3.  
    
4.  
   dai$ea[las] <- 2 * axa
5.  
    
6.  
   # 重新生成初始圆的顶点数据，添加一列
7.  
   # 表示一个圆是固定的还是自由的
8.  
   dnta <- cres(dain, ste = "area")
9.  
    
10.  
    dani$sae <- iflse(dtgtd %in% laid, "fixed", "free")
11.  
     
12.  
    # 现在使用权重向量重新运行布局算法以固定位置
13.  
    # 最大的圆
14.  
     
15.  
    res <- cirtt.t
16.  
     
17.  
    dgfal <- circes(es$aut)
18.  
     
19.  
     
20.  
    plot(dta = da,as(x, y, grp=d, fl=ste)) +
21.  
     
22.  
    gen(coor)
23.  
     

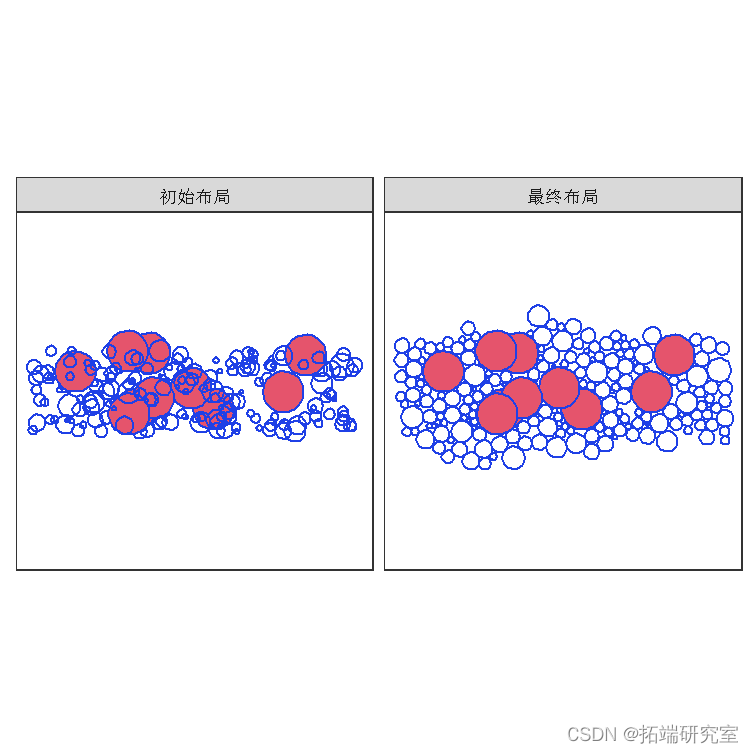
请注意，在初始布局中重叠的固定圆在最终布局中仍然重叠。

---

最受欢迎的见解

1.R语言动态图可视化：如何、创建具有精美动画的图

2.R语言生存分析可视化分析

3.Python数据可视化-seaborn Iris鸢尾花数据

4.r语言对布丰投针（蒲丰投针）实验进行模拟和动态

5.R语言生存分析数据分析可视化案例

6.r语言数据可视化分析案例：探索brfss数据数据分析

7.R语言动态可视化：制作历史全球平均温度的累积动态折线图动画gif视频图

8.R语言高维数据的主成分pca、 t-SNE算法降维与可视化分析案例报告

9.python主题LDA建模和t-SNE可视化