【快速幂】斐波那契数列

快速幂运算：

　　快速幂的目的就是做到快速求幂，假设我们要求a^b,按照朴素算法就是把a连乘b次，这样一来时间复杂度是O(b)也即是O(n)级别，快速幂能做到O(logn)，快了好多好多。它的原理如下：

　　假设我们要求a^b，那么其实b是可以拆成二进制的，该二进制数第i位的权为2^(i-1)，例如当b==11时：

　　　　 a¹¹=a^{(2^0+2^1+2^3)}

　　11的二进制是1011，11 = 2³×1 + 2²×0 + 2¹×1 + 2º×1，因此，我们将a¹¹转化为算式 a^{2^0}*a^{2^1}*a^{2^3}，也就是a¹*a²*a⁸ ，看出来快的多了吧原来算11次，现在算三次，其中a¹  a²  a⁸的计算方式代码注释里面写着。

　　代码：

public class NExponent {

    public static void main(String[] args) {
        System.out.println(ex2(2, 3));
    }
    
    public static int ex(int a,int n){
        if(n==0)return 1;
        if(n==1)return a;
        int temp = a; // a的1次方
        int res = 1;
        int exponent = 1;
        while((exponent<<1)<n){
            temp = temp * temp;
            exponent = exponent << 1;
        }
        res *= ex(a,n-exponent);
        return res * temp;
    }
    
    /**
     * 快速幂  O(lgn)
     */
    public static long ex2(long n,long m){
        if(n==0) return 1;
        long pingFangShu = n; // n 的 1 次方
        long result = 1;
        while (m != 0) {
            // 遇1累乘现在的幂
            if ((m & 1) == 1)
                result *= pingFangShu;
            // 每移位一次，幂累乘方一次
            pingFangShu = pingFangShu * pingFangShu;
            // 右移一位
            m >>= 1;
        }
        return result;
    }
}

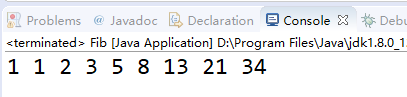
题目：矩阵快速幂求解斐波那契数列

　　

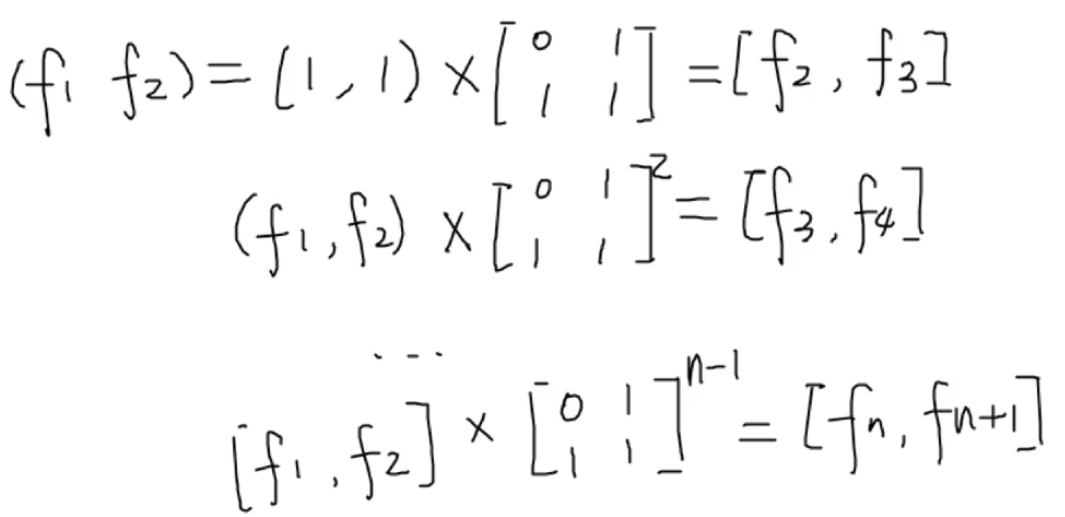
　　代码：

public class Fib {

    public static void main(String[] args) {
        for (int i = 1; i < 10; i++) {
            System.out.print(fib(i)+" ");
        }
    }
    
    // 矩阵运算求解斐波那契数列
    static long fib(long n){
        if (n == 1 || n == 2) return 1;
        long[][] matrix = { 
                { 0, 1 }, 
                { 1, 1 } 
                };
        long[][] res = matrixPower(matrix, n - 1);// 乘方
        res = matrixMultiply(new long[][] { { 1, 1 } }, res);// 矩阵相乘
        return res[0][0];
    }
    
    public static long[][] matrixPower(long[][] matrix, long p) {
        // 初始化结果为单位矩阵，对角线为1
        long[][] result = new long[matrix.length][matrix[0].length];
        // 单位矩阵，相当于整数的1
        for (int i = 0; i < result.length; i++) {
            result[i][i] = 1;
        }

        // 平方数
        long[][] pingFang = matrix; // 一次方
        while (p != 0) {
            if ((p & 1) != 0) { // 当前二进制位最低位为1，将当前平方数乘到结果中
                result = matrixMultiply(result, pingFang);//
            }
            // 平方数继续上翻
            pingFang = matrixMultiply(pingFang, pingFang);
            p >>= 1;
        }
        return result;
    }
    
    /**
     * 矩阵乘法 矩阵1为n*m矩阵，矩阵2为m*p矩阵 结果为n*p矩阵
     */
    public static long[][] matrixMultiply(long[][] m1, long[][] m2) {
        final int n = m1.length;
        final int m = m1[0].length;
        if (m != m2.length)
            throw new IllegalArgumentException();
        final int p = m2[0].length;

        long[][] result = new long[n][p];// 新矩阵的行数为m1的行数，列数为m2的列数

        for (int i = 0; i < n; i++) {// m1的每一行
            for (int j = 0; j < p; j++) {// m2的每一列
                for (int k = 0; k < m; k++) {
                    result[i][j] += m1[i][k] * m2[k][j];
                }
            }
        }
        return result;
    }

}

　　结果：