定义
树(Tree)是n(n≥0)个结点的有限集合,n=0时称为空树。在任意一个非空树中:①有且只有一个特定的称为根(root)的结点;②当n>1时,其余结点可以分为m(m>0)个互不相交的有限集T₁,T₂,T₃....Tп,其中每个集合本身又是一棵树,并且称为根的子树(subTree)


树的定义用到了递归,也就是在树的的定义中还用到了树的概念,如上图中T₁,T₂的树就是结点A的子树,DGHI组成的树是结点B的子树,EJ组成的树是结点C的子树。当n>0时根节点时唯一的,当m>0,子树个数没有限制,但一定不能相交。
结点分类
树的结点包含一个数据元素及若干指向其子树的分支。结点拥有的子树数称为结点的度(Degree)。度为0的结点称为叶结点(Leaf)或终端结点;度不为0的结点称为非终端结点或分支结点。除根结点之外,分支结点也称为内部结点。树的度是树内各结点的度的最大值。如下图,这棵树的度的值为最大结点D的度,也就是3

结点关系
结点的子树的根称为该结点的孩子(Child),相应的该结点称为孩子的双亲(Parent),同一个双亲的孩子之间互称兄弟(Sibling),结点的祖先是从根到该结点所经分支上的所有结点,以某结点为根的的子树任意一个结点都是该结点的子孙。如下图:对于H来说,D,B,A都是它的祖先,而B的子孙有D,G,H,I

其他概念
结点的层次(Level)从根开始定义,根为第一层,根的子节点称为第二层,其双亲结点在同一层的结点互为堂兄弟,如下图:D,E,F是堂兄弟,G,H,I,J也是。树中结点的最大层次称为树的深度(Depth)或高度,当前树高度为4。

如果我们将树中的各个子树看成从左至右依次有顺序的,不能互换,那么该树为有序树,否则就是无序树。
森林(Forest)是m(m≥0)棵互不相交的树的集合,对于树中的每个结点而言,其子树的集合即为森林。
线性结构与树结构的对比:

树的存储结构
对于存储结构,可能会联想到前面的顺序存储和链式存储结构。但是对于数这种可能会有很多孩子的特殊数据结构,只用顺序存储结构或者链式存储结构很那实现,那么可以将这两者结合,产生主要的三种存储结构表示法:双亲表示法、孩子表示法、孩子兄弟表示法。
双亲表示法:
假设以一组连续空间存储数的结点,同时在每个结点中,附设一个指示器指示其双亲结点到链表中的位置。
| data(数据域) | parent(指针域) |
|---|---|
| 存储结点的数据信息 | 存储该结点的双亲所在数组中的下标 |
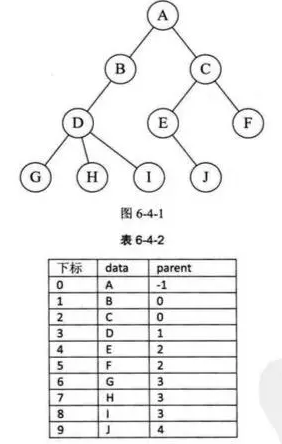
双亲表示法的特点
- 由于根结点是没有双亲的,约定根结点的位置位置域为-1.
- 根据结点的
parent指针很容易找到它的双亲结点。所用时间复杂度为O(1),直到parent为-1时,表示找到了树结点的根。 - 缺点:如果要找到孩子结点,需要遍历整个结构才行。
双亲表示法存储结构代码实现:
public class TreeParent<E> {
public static class Node<T> {
T data;
// 保存其父节点的位置
int parent;
public Node() {
}
public Node(T data) {
this.data = data;
}
public Node(T data, int parent) {
this.data = data;
this.parent = parent;
}
public String toString() {
return "TreeParent$Node[data=" + data + ", parent=" + parent + "]";
}
}
private final int DEFAULT_TREE_SIZE = 100;
private int treeSize = 0;
// 使用一个Node[]数组来记录该树里的所有节点
private Node<E>[] nodes;
// 记录树的节点数
private int nodeNums;
// 以指定节点创建树
public TreeParent(E data) {
treeSize = DEFAULT_TREE_SIZE;
nodes = new Node[treeSize];
nodes[0] = new Node<E>(data, -1);
nodeNums++;
}
// 以指定根节点、指定treeSize创建树
public TreeParent(E data, int treeSize) {
this.treeSize = treeSize;
nodes = new Node[treeSize];
nodes[0] = new Node<E>(data, -1);
nodeNums++;
}
}孩子表示法:
把每个结点的孩子结点排列起来,以单链表作为存储结构,则n个结点有n个孩子链表,如果是叶子结点则此单链表为空。然后n个头指针又组成一个线性表,采用顺序存储结构,存放进一个一维数组中。

孩子表示法要设计两种结点结构:孩子链表的孩子结点和表头数组的表头结点
- 孩子链表的孩子结点
| child(数据域) | next(指针域) |
|---|---|
| 存储某个结点在表头数组中的下标 | 存储指向某结点的下一个孩子结点的指针 |
- 表头数组的表头结点
| data(数据域) | firstchild(头指针域) |
|---|---|
| 存储某个结点的数据信息 | 存储该结点的孩子链表的头指针 |
孩子表示法的存储结构:
public class TreeChild<E> {
// 子节点类
private static class SonNode {
// 当前节点位置
private int pos;
// 下一节点
private SonNode next;
public SonNode(int pos, SonNode next) {
this.pos = pos;
this.next = next;
}
}
// 表头结构
public static class Node<T> {
// 节点数据
T data;
// 第一个子节点
SonNode first;
public Node(T data) {
this.data = data;
this.first = null;
}
// 默认树的节点数
private final int DEFAULT_SIZE = 100;
// 树的节点数
private int treeSize = 0;
// 存储树节点的节点数组
private Node<E>[] nodes;
// 记录的节点数
private int nodeNum = 0;
// 指定根节点创建树
public TreeChild(E element) {
treeSize = DEFAULT_SIZE;
nodes = new Node[treeSize];
nodes[0] = new Node<E>(element);
nodeNum++;
}
}对于孩子表示法,查找某个结点的某个孩子,或者找某个结点的兄弟,只需要查找这个结点的孩子单链表即可。但是当要寻找某个结点的双亲时,就不是那么方便了。所以可以将双亲表示法和孩子表示法结合,就是在表头数组再添加一列存放双亲的下标,形成双亲孩子表示法。

孩子兄弟表示法:
任意一棵树,它的结点的第一个孩子如果存在就是唯一的,它的右兄弟存在也是唯一的。因此,设置两个指针,分别指向该结点的第一个孩子和此结点的右兄弟。
| data(数据域) | firstchild(指针域) | rightsib(指针域) |
|---|---|---|
| 存储结点的数据信息 | 存储该结点的第一个孩子的存储地址 | 存储该结点的右兄弟结点的存储地址 |

孩子兄弟数据结构:
public class TreeNode {
private TreeNode sonNode;//这里存储的是最左的儿子节点
private TreeNode brotherNode;//这里存储的是自己的兄弟节点
private int value;
public TreeNode(TreeNode sonNode,TreeNode brotherNode,int value){
this.sonNode = sonNode;
this.brotherNode = brotherNode;
this.value = value;
}
public TreeNode getSonNode(){
return this.sonNode;
}
public TreeNode getBrotherNode() {
return brotherNode;
}
public int getValue(){
return value;
}
public void setSonNode(TreeNode sonNode){
this.sonNode = sonNode;
}
public void setBrotherNode(TreeNode brotherNode){
this.brotherNode = brotherNode;
}
这种表示方法,只要通过fistchild找到此结点的长子,在通过长子结点的rightsib找到它的二弟,然后一直下去,直到找到自己的孩子,这种表示法最大的好处就是把一个复杂的树变成了一棵二叉树,上图可以变为下图的样子:

这样就能利用二叉树的特性和算法来处理该树了。